A key assumption underpinning generalized linear models (which linear regression is a type of) is the independence of observations. In longitudinal data this will simply not hold. Observations within an individual (between time points) are likely to be more similar than those between individuals.

支持广义线性模型 (线性回归是一种类型)的关键假设是观测的独立性。 在纵向数据中，这根本不成立。 个人内部(时间点之间)的观察可能比个人之间的观察更相似。

So, how do you deal with this? One option is to fit a generalized linear mixed model in which there are random intercept and slope terms for each individual. This will tell you for a specific individual (i.e. conditional on the random intercept and slope) what is the effect of a variable on an outcome. However, this isn’t very useful if you are concerned with the marginal effect, i.e. what is the effect of a variable on an outcome on average in the population.

那么，您如何处理呢？ 一种选择是拟合广义线性混合模型，其中每个人都有随机的截距和斜率项。 这将告诉您特定的个体(即以随机截距和斜率为条件)，变量对结果的影响是什么。 但是，如果您关注边际效应，即变量对总体平均结果的影响是什么，这不是很有用。

If you want to answer these population questions you need to fit a generalized linear model using generalized estimating equations (GEE). This is an approach that obtains the population average effect accounting for the fact that observations within individuals are likely to be more similar than those between individuals.

如果要回答这些总体问题，则需要使用广义估计方程 (GEE)拟合广义线性模型。 这是一种获得人口平均效应的方法，说明了一个事实，即个人内部的观察可能比个人之间的观察更相似。

一个例子 (An example)

Suppose we have our outcome — all-cause mortality. Now suppose we record this every month for 10 months for every person. Now suppose our exposure, which is just time. We can now define a logistic regression model, with the sole independent variable being time (in months) and the dependent variable being death at that time. “Okay, great” I hear you say “but these observations are obviously not independent!”. Spot on, but we’ll come to that.

假设我们有结果 -全因死亡率。 现在假设我们每个人每个月记录一次，持续10个月。 现在假设我们的曝光，这只是时间。 现在，我们可以定义一个逻辑回归模型，唯一的自变量为时间(以月为单位)，因变量为当时的死亡。 “好极了，”我听到你说“但是这些观察结果显然不是独立的！”。 当场，但是我们来谈谈。

工作相关结构 (Working correlation structures)

To use GEE we must first define how time points are related. However, by using Huber-White standard errors our results will be consistent even if we misspecify this relationship! So we have some choices.

要使用GEE，我们必须首先定义时间点之间的关系。 但是，通过使用Huber-White标准误差，即使我们未正确指定此关系，我们的结果也将保持一致 ！ 所以我们有一些选择。

独立 (Independent)

This working correlation structure assumes that time points are independent of each other. This is probably an unreasonable assumption in practice.

该工作相关结构假定时间点彼此独立。 实际上这可能是一个不合理的假设。

可交换的 (Exchangeable)

This is where the correlation between observations at two time points is equal for any two time points. This is commonly used as it requires just one additional parameter α to be estimated.

这是任意两个时间点在两个时间点的观测值之间的相关性相等的地方。 这是常用的，因为它仅需要估计一个附加参数α。

自回归 (Autoregressive)

This is where the correlation between observations follows an autoregressive structure. Suppose we were using an AR-1 correlation matrix. This would mean that the correlation between month 1 and 2 of a person would be expected to be α and the correlation between month 1 and 3 of a person would be expected to be α², between month 1 and 4 would be α³ and so on.

这是观测值之间的相关遵循自回归结构的地方。 假设我们使用的是AR-1相关矩阵。 这意味着一个人的第1个月和第2个月之间的相关性预计为α，一个人的第1个月和第3个月之间的相关性预计为α2，第1个月和第4个月之间的相关性为α3，依此类推。

This is most appropriate when you think closer together time points are more similar than further apart time points.

当您认为更靠近的时间点比更远的时间点更相似时，这是最合适的。

非结构化 (Unstructured)

This is where we estimate a separate α for each possible combination of time points. This is the most general case. Though you need a lot of data to be able to estimate all of the α used.

在这里，我们为每个可能的时间点组合估计一个单独的α。 这是最一般的情况。 尽管您需要大量数据才能估计所有使用的α。

其他选择 (Other choices)

There do exist some other choices, but these aren’t widely used.

确实存在其他选择，但并未广泛使用。

如何选择使用哪一个？ (How to choose what one to use?)

It’s simple. Either choose the most general one your data can support (depending on sample size) or you can choose one you think suits the data best. Either way, don’t sweat it! This approach is consistent even if you misspecify this.

这很简单。 选择您的数据可以支持的最通用的一种(取决于样本量)，也可以选择您认为最适合该数据的一种。 无论哪种方式，都不要流汗！ 即使您没有正确指定，这种方法也是一致的。

如何拟合模型 (How to fit the model)

Fitting the model is simple. We just fit a GLM using GEE with our specified working correlation matrix:

拟合模型很简单。 我们仅使用GEE和指定的工作相关矩阵来拟合GLM：

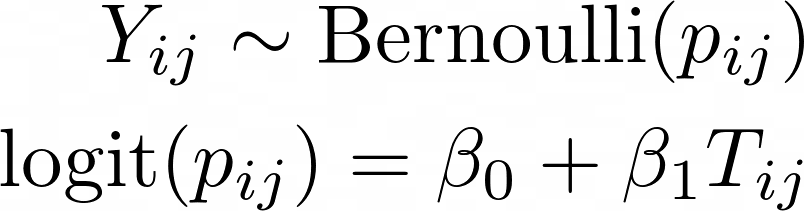
Where:

哪里：

• Yij is 1 if participant i died at time j
  如果参与者我在时间j死亡，则Yij为1
• pij is the probability of death for participant i at time j
  pij是参与者i在时间j的死亡概率
• β0 is the population average log odds of death at time 0. This can be exponentiated to obtain the odds of death at time 0.
  β0是时间0的总体平均对数死亡几率。可以对它进行幂运算以获得时间0的死亡几率。
• β1 is the population average difference in log odds of death associated with a one-month increase in time. This can be exponentiated to obtain the odds ratio associated with a one-month increase in time.
  β1是与一个月的时间增加相关的人口平均对数死亡率的差异。 可以将其取幂以获得与一个月时间增加相关的优势比。
• Tij is the time of the j’th measurement for participant i in months.
  Tij是参加者i的第j个测量时间，以月为单位。

That’s it. Our population average effect of a one-month increase on time increases the odds of death by an odds ratio of exp(β1).

而已。 我们的人口平均时间增加一个月会增加死亡几率，使之成为几率exp(β1)。

在R中拟合模型 (Fitting a model in R)

We can do this in R using geepack. Suppose our dataframe already existed with three columns death time and person.id all we have to do is:

我们可以使用geepack在R中做到这一点 。 假设我们的数据框已经存在，其中有三列death time和person.id我们要做的就是：

library(geepack)
mod <- geeglm(death ~ time, id = person.id, waves = time, family=binomial, corstr="exchangeable")

You can then just call summary(mod) as normal and get your results!

然后，您可以像平常一样仅调用summary(mod)并获得结果！

And of course, you could add covariates to the model by just adding them to the formula. They can be time-varying or constant — either is fine!

当然，您可以通过将协变量添加到公式中来将协变量添加到模型中。 它们可以是时变的，也可以是恒定的-都可以！

结论 (Conclusion)

Hopefully you’ve come away from reading this with a basic idea of GEE. They should be a tool in the toolbox of any data scientist working with longitudinal data.

希望您已经阅读了有关GEE的基本概念后再阅读。 它们应该是使用纵向数据的任何数据科学家工具箱中的工具。