One of the most beautiful concepts in statistics and probability is Central Limit Theorem,people often face difficulties in getting a clear understanding of this and the related concepts, I myself struggled understanding this during my college days (eventually mugged up the definitions and formulas to pass the exam). In its core it is a very simple yet elegant theorem that enables us to estimate the population mean. Here I will try to explain these concepts using this toy dataset on customer demographics available on Kaggle (this is a fictional dataset created for educational purposes). Without wasting much time lets dive in and try to understand what CLT is

统计量和概率中最美丽的概念之一是中央极限定理 ，人们常常在难以清楚地理解这一概念和相关概念时遇到困难，我本人在上大学期间一直难以理解这一概念(最终弄糟了要通过的定义和公式考试)。 其核心是一个非常简单而优雅的定理，使我们能够估计总体均值。 在这里，我将尝试在Kaggle上提供的有关客户受众特征的玩具数据集中解释这些概念(这是为教育目的而创建的虚构数据集)。 不要浪费太多时间，让我们深入研究一下CLT是什么

中心极限定理 (CENTRAL LIMIT THEOREM)

Here is what Central Limit Theorem states

这是中心极限定理指出的

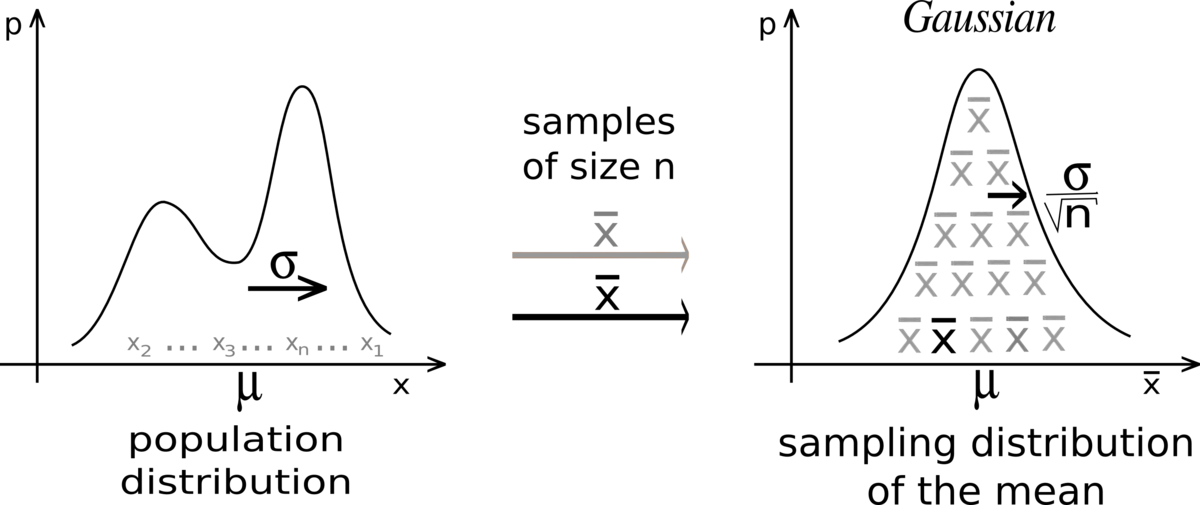
If you take sufficiently large samples from a distribution,then the mean of these samples would follow approximately normal distribution with mean of distribution approximately equal to population mean and standard deviation equal on 1/√n times the population standard deviation (here n is number of elements in a sample)

如果从分布中获取足够大的样本，则这些样本的均值将遵循近似正态分布，分布均值大约等于总体均值，标准偏差等于总体标准偏差的1 /√n倍(此处n是样本中的元素)

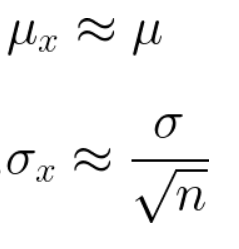
Now comes the fun part, in order to have a better understanding and appreciation of the above statement, let us take our toy dateset (will take the annual income column for our analysis) and try to check if these approximations actually holds true.

现在是有趣的部分，为了更好地理解和理解上述说法，让我们以玩具的日期集(将采用“年收入”列进行分析)并尝试检查这些近似值是否正确。

We will try to estimate the mean income of a population, first let us have a look at the distribution and size the population

我们将尝试估算人口的平均收入，首先让我们看一下人口的分布和规模

df = pd.read_csv(r'toy_dataset.csv')
print("Number of samples in our data: ",df.shape[0])
sns.kdeplot(df['Income'],shade=True)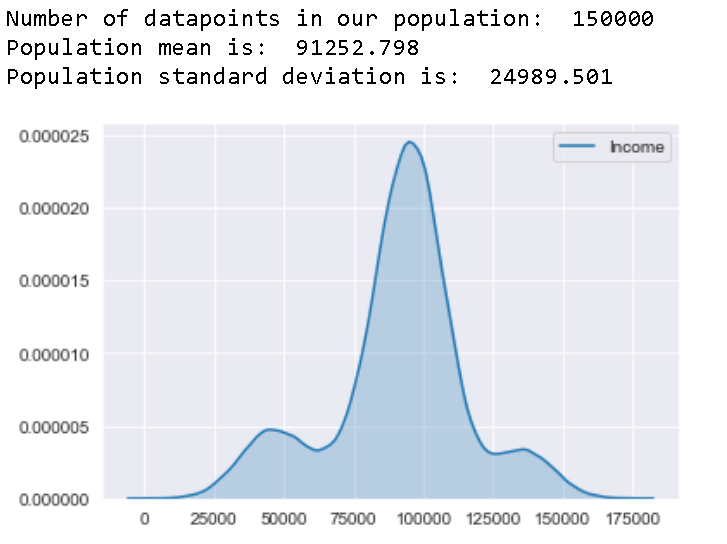

Well, we can fairly say this is isn’t exactly a normal distribution and the original population mean and standard deviation is 91252.798 and 24989.501 respectively. Now have a good look on to these numbers and let’s see if we could use Central Limit Theorem to approximate these values

好吧，我们可以很公平地说这不是正态分布，原始总体均值和标准差分别为91252.798和24989.501 。 现在看一下这些数字，让我们看看是否可以使用中心极限定理来近似这些值

生成随机样本 (GENERATING RANDOM SAMPLES)

Now let us try to generate random samples from the population and try to plot sample mean distributions

现在让我们尝试从总体中生成随机样本，并尝试绘制样本均值分布

def return_mean_of_samples(total_samples,element_in_each_sample):
    sample_with_n_elements_m_size = []
    for i in range(total_samples):
        sample = df.sample(element_in_each_sample).mean()['Income']
        sample_with_n_elements_m_size.append(sample)
    return (sample_with_n_elements_m_size)

We will use this function to generate random sample means and later use it to calculate sampling distributions

我们将使用此函数生成随机样本均值，然后使用它来计算采样分布

Here we are taking 200 samples with 100 elements in each samples and see how the sample mean distribution looks like

在这里，我们以200个样本为例，每个样本中有100个元素，并查看样本均值分布如何

sample_means = return_mean_of_samples(200,100)
sns.kdeplot(sample_means,shade=True)
print("Total Samples: ",200)
print("Total elements in each sample: ",100)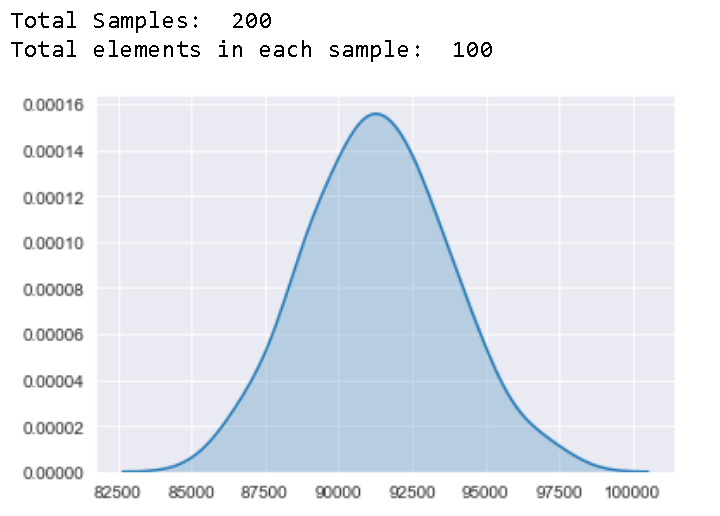

Well that looks pretty normal, so now we can assume that with sufficient sample size, sample means do follow normal distribution irrespective ofthe original distributions

好吧，这看起来很正常，因此现在我们可以假设，在有足够的样本量的情况下，样本均值确实遵循正态分布，而与原始分布无关

Now comes the second part, let us try to see if we could estimate the population mean from this sampling distribution, below is a piece of code that generates different sampling distributions by varying total sample size and elements in each samples

现在是第二部分，让我们尝试看看是否可以从该采样分布中估计总体平均值，下面是一段代码，该代码通过改变总采样大小和每个采样中的元素来生成不同的采样分布

total_samples_list = [100,500]
elements_in_each_sample_list = [50,100,500]
mean_list = []
std_list = []
key_list = []
estimate_std_list = []
key=''
pop_mean = [population_mean]*6
pop_std = [population_std]*6
for tot in total_samples_list:
    for ele in elements_in_each_sample_list:
        key = '{}_samples_with_{}_elements_each'.format(tot,ele)
        key_list.append(key)
        mean_list.append(np.round(np.mean(return_mean_of_samples(tot,ele)),3))
        std_list.append(np.round(np.array(return_mean_of_samples(tot,ele)).std(),3))
        estimate_std_list.append(np.round(population_std/(np.sqrt(ele)),3))pd.DataFrame(zip(key_list,pop_mean,mean_list,pop_std,estimate_std_list,std_list),columns=['Sample_Description','Population_Mean','Sample_Mean','Population_Standard_Deviation',"Pop_Std_Dev/"+u"\u221A"+"sample_size",'Sample_Standard_Deviation'])

• Look at second and third columns, we can clearly see the mean of sampling distribution is very close to the population mean in all the distributions
  查看第二和第三列，我们可以清楚地看到抽样分布的均值与所有分布中的总体均值非常接近
• Have a look at the last two columns, initially there is some difference in the deviations but as the sample size increases this difference becomes negligible
  看看最后两列，最初的偏差有所不同，但是随着样本数量的增加，这种差异可以忽略不计

Let us further plot these sampling distributions and population mean and see how the plots look

让我们进一步绘制这些采样分布和总体均值，并查看这些图的外观

def plot_distribution(sample,population_mean,i,j,color,sampling_dist_type):
    sns.kdeplot(np.array(sample),color = color,ax = axs[i,j],shade=True)
    axs[i, j].axvline(population_mean, linestyle="-", color='r', label="p_mean")
    axs[i, j].axvline(np.array(sample).mean(), linestyle="-.", color='b', label="s_mean")
    axs[i, j].set_title(key)
    axs[i, j].legend()colors = ['r','g','b','y', 'c', 'm', 'k']
plt_grid  = [(0,0), (0, 1), (1, 0), (1, 1), (2, 0), (2, 1)]
sample_sizes = [(100,50), (100, 100), (100, 500), (500, 50), (500, 100), (500, 500)]total_samples_list = [100,500]
elements_in_each_sample_list = [50,100,500]fig, axs = plt.subplots(3, 2,  figsize=(10, 9))
i = 0
for tot in total_samples_list:
    for ele in elements_in_each_sample_list:
        key = '{}_samples_with_{}_elements_each'.format(tot,ele)
        plot_distribution(return_mean_of_samples(tot,ele), population_mean , plt_grid[i][0], plt_grid[i][1] , colors[i], key)
        i = i + 1
plt.show()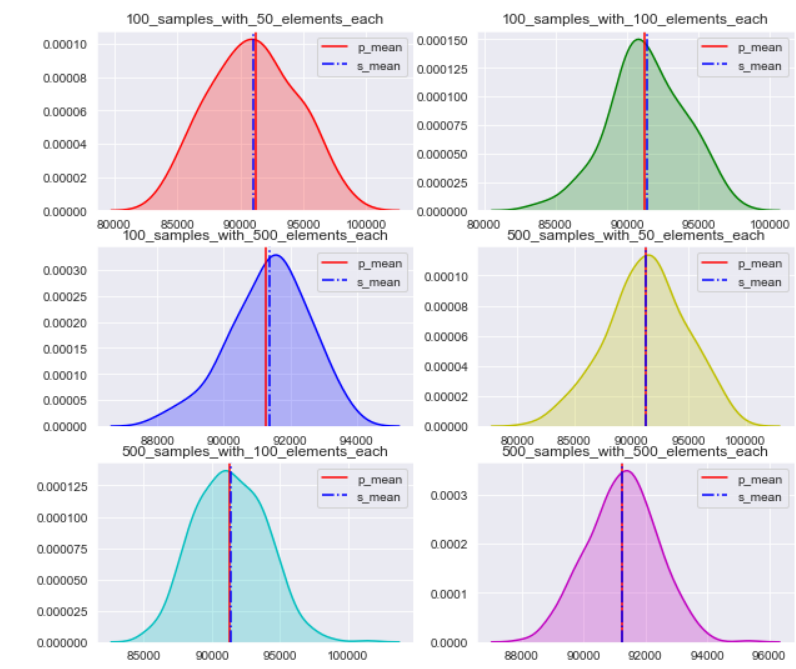

As you can see the mean of sampling distribution is pretty close to the population mean. (Here is a food for thought, have a look at first and last plots do you notice there is a difference in spread of data, first one is more spread around population mean as compared to last, look at the scale on x axis for better clarity, well once your reach the end of this blog try to answer this question yourself)

如您所见，抽样分布的平均值非常接近总体平均值。 ( 这是一个值得深思的地方，请查看第一和最后一个图，您是否注意到数据分布上的差异，第一个是在人口均值上的分布比最后一个更大，请查看x轴上的比例更好清楚，一旦您到达本博客的结尾，尝试自己回答这个问题 )

保密间隔 (CONFIDENCE INTERVAL)

A confidence interval can be defined as an entire interval of plausible values of a population parameter, such as mean based on observations obtained from a random sample of size n.

置信区间可以定义为总体参数的合理值的整个区间，例如基于从大小为n的随机样本获得的观察值的平均值。

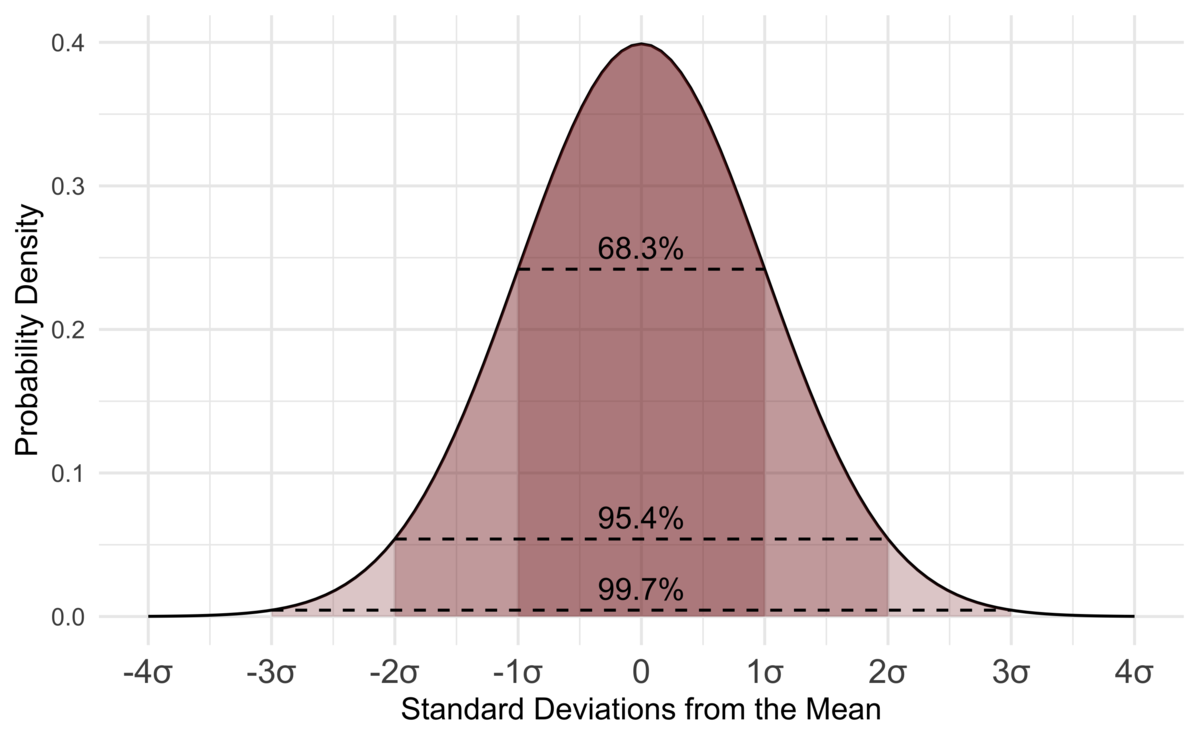
Let’s summarize our leanings so far and and try to understand Confidence Intervals from it.

让我们总结到目前为止的观点，并尝试从中了解置信区间。

• Sampling distribution of mean of samples follow a normal distribution
  样本均值的抽样分布遵循正态分布

• Hence using property of normal distribution 95% of sample means lie within two standard deviations of population mean

  因此，使用正态分布特性， 样本均值的95％处于总体均值的两个标准差之内

• We can rephrase the sentence and say that 95% of these Intervals or rather Confidence Intervals (two standard deviations away from the mean on either side) contains the population mean

  我们可以改写句子，说95％的这些区间或置信区间(两侧的均值有两个标准差)包含总体均值

Here I would like to give more focus on the last point we talked about. People often get confused and say once we take a random sample and calculate its mean and corresponding 95% CI, there is a 95% chance that the population mean lies within 2 standard deviations of this sample mean, this statement is wrong

在这里，我想更加关注我们刚才谈到的最后一点。 人们常常会感到困惑，说一旦我们抽取了一个随机样本并计算出其均值和相应的95％CI，总体均值就有95％的机会位于该样本均值的2个标准差之内，这是错误的

When we talk about a probability estimate w.r.t to a sample then that sample gets fixed here (including the corresponding sample mean and confidence interval), also population mean eventually is a fixed value, hence there is no point in saying there is a 95% probability of a fixed point (population mean) lying in a fixed interval (CI of sample used), it would either exist there or not, instead the more proper definition of 95% CI is

当我们谈论样本的概率估计值时，样本在此处固定( 包括相应的样本均值和置信区间 )，总体均值最终也是固定值，因此，毫无疑问地说概率为95％固定间隔(使用的样本的CI)中的固定点(人口平均值)的平均值，则该值是否存在或不存在，取而代之的是更准确地定义95％CI

If random samples are taken and corresponding sample means and CI’s (two standard deviations from the mean on either side) are calculated, then 95% of these CI’s would contain the population mean. For example let’s say we take 100 random samples and calculate their CI’s then 95% of these CI’s would contain the population mean

如果抽取随机样本并计算出相应的样本均值和CI(任一侧均值有两个标准差)，则这些CI的95％将包含总体均值。 例如，假设我们抽取100个随机样本并计算其CI，则这些CI中的95％将包含总体均值

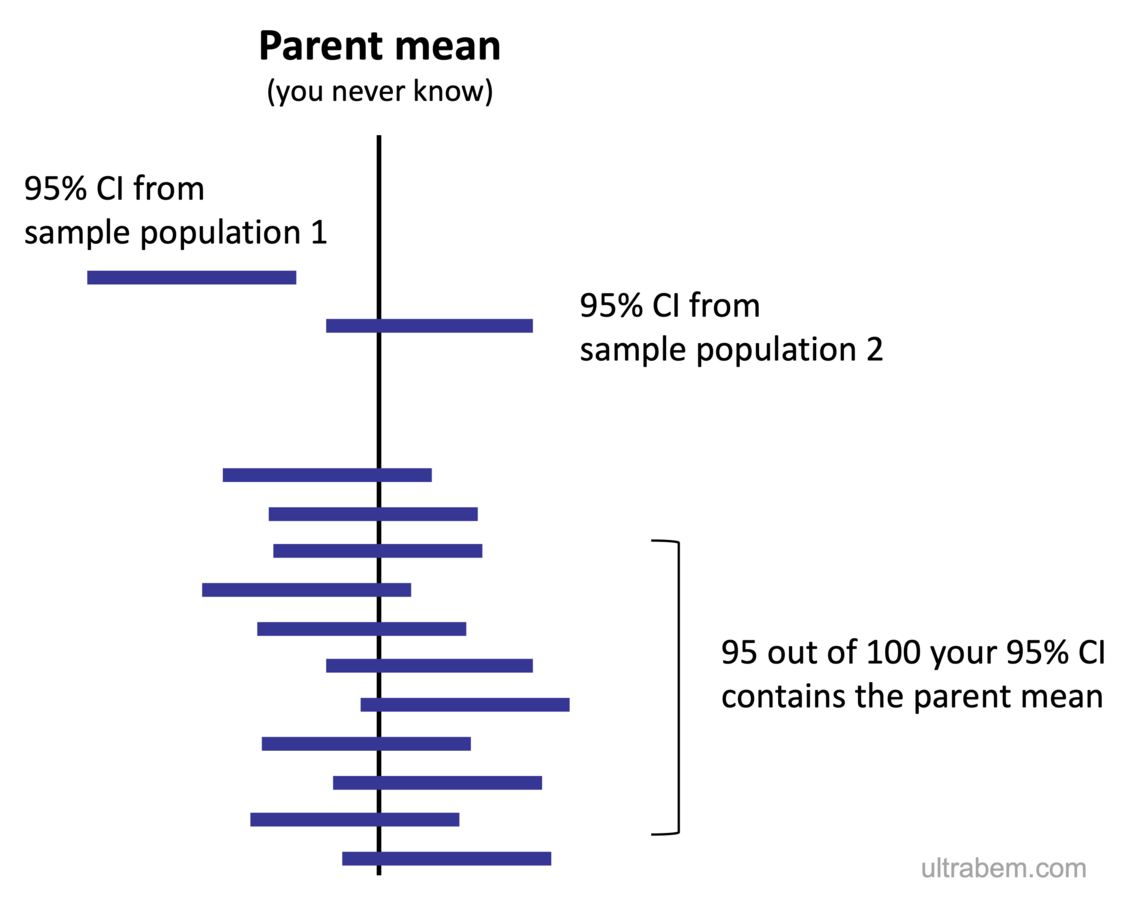
Enough of the talking business, now as always lets take our toy dataset and see if this holds true.

足够多说话的生意了，现在像往常一样让我们获取玩具数据集，看看这是否成立。

def get_CI_percent(size):
    counter = 0
    for i in range(size):
        is_contains = False
        sample_mean = df.sample(50)['Income'].mean()
        lower_lim = sample_mean - 2*standard_error
        upper_lim = sample_mean + 2*standard_error
        if (population_mean>=lower_lim)&(population_mean<=upper_lim):
            is_contains = True
            counter = counter + 1    
    return  np.round(counter/size*100,2)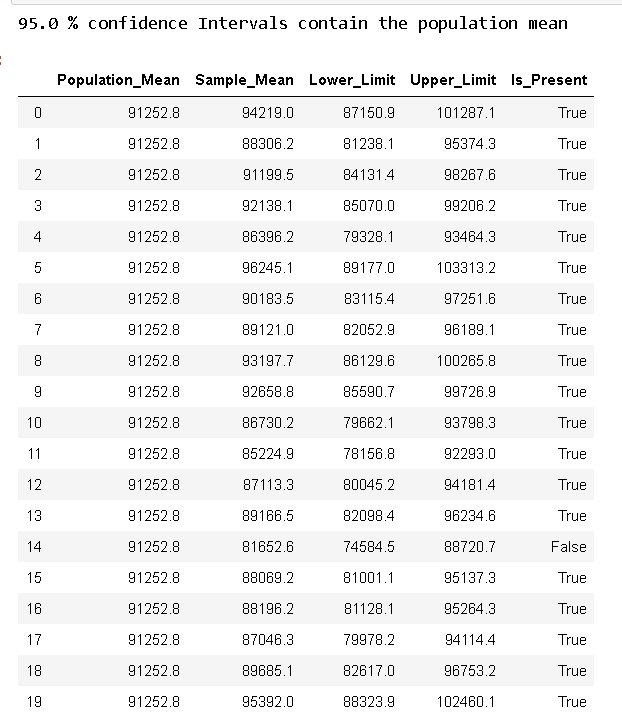 

I took 20 random samples with 50 elements in each sample and calculated their sample means and respective two standard deviation intervals (95% CI’s), 18 out of 20 intervals contained these intervals. (actually this interval count varied between 18–20)

我抽取了20个随机样本，每个样本中包含50个元素，并计算了它们的样本均值和两个标准差区间(95％CI)，其中20个区间中有18个包含这些区间。 (实际上，此间隔计数在18–20之间变化)

Instead of giving a point estimate (taking a sample and calculating its mean), it is more plausible to give an interval estimate (this helps us include any error that might occur due to sampling) hence we calculate these confidence intervals along with the sample mean.

与其给出点估计(获取样本并计算其均值)，不如给出区间估计(这有助于我们包括由于采样而可能出现的任何误差)，因此我们将这些置信区间与样本均值一起计算。

结论 (CONCLUSION)

One question that some of you might be having, why go through so much hard work of taking random samples, calculating its sample mean hence the Confidence Interval later, why not simply do np.mean() like it was done in the very first line of code here.

你们中的一些人可能会遇到一个问题，为什么要经过如此艰巨的工作来抽取随机样本，然后计算其样本均值，从而得出置信区间，为什么不像第一行那样简单地做np.mean()代码在这里。

Well if you have your data completely available in digital form and you could calculate your population metric just from a single line of code within milliseconds then definitely go for it there is no point in going through the whole process

好吧，如果您的数据完全以数字形式提供，并且您可以仅在几毫秒内通过单行代码来计算人口指标，那么绝对可以，整个过程没有意义

However there are many scenarios where data collection itself is a big challenge, suppose we want to estimate mean height of people in Bangalore then it is practically impossible to go to every person and record the data. This is where these concepts of sampling, Confidence Intervals are really useful.

但是，在很多情况下，数据收集本身就是一个很大的挑战，假设我们要估算班加罗尔的平均人口高度，那么几乎不可能到每个人那里记录数据。 这是抽样，置信区间这些概念真正有用的地方。

Here is the link to the code file and the dataset. For those of you who are new to these topics, I would strongly recommend to try running the code yourself, play around with the dataset (there are other fields like age) to get a better understanding.

这是代码文件和数据集的链接 。 对于那些不熟悉这些主题的人，我强烈建议您自己尝试运行代码，并尝试使用数据集(还有age等其他字段)以更好地理解。