图像特征提取——韦伯局部描述符（WLD）

一、原理及概述

　　韦伯局部描述符（WLD）是一种鲁棒性好、简单高效的局部特征描述符。WLD由两个部分组成：差分激励和梯度方向。

　　其具体算法是对于给定的一幅图像，通过对每个像素进行这两个分量的计算来提取其差分激励图像和梯度方向图像，并将这两部分组合成一个二维直方图，进而转化为一个一维直方图，最后利用一维直方图进行分类。[1]

 

　　差分激励：差分激励时某像素领域值和减去8倍中心像素值的结果与该像素点的比值。显然，这反映了当前像素点与领域像素点之间的差异。

　　在对差分激励有了一个概念性的认识以后，我们来看数学表述：

 

　　综合上述公式，我们整合一下：

　　通过计算式子，我们知道如果Garctan>0，则表明领域像素的亮度大于当前像素；反之，则表明当前像素在该区域内的亮度较低。

　　在计算过程中，为了避免出现输入值过大或过小的情况从而造成不可控的局面，可以通过一个函数将其映射到一个合理范围之内。常用的是sigmoid函数、arctan函数以及对数函数。sigmoid函数如下：

　　由于考虑到sigmoid函数的计算量较大，所以往往可以选用arctan函数。

 

　　梯度方向：通过计算局部窗内水平方向和垂直方向像素插值之比的反正切变换得到[1]。梯度方向反映的是局部窗内灰度变化的空间分布信息。

　　以下为梯度方向的数学表述，注意，xi在下面一张图里。

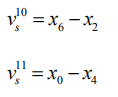
　　为了更加有效地区分灰度窗内灰度变化的分布情况，，我们需要将其扩展到[0,2pi)。设映射f：，有：

　　最后，需要对其量化，计算过程如下：

 

　　直方图：在图像中利用直方图表示灰度分布。在此处，直方图是用于局部描述算子的变量之一。

　　我们在得到了差分激励与梯度方向以后，可以得到两幅新的图像：差分激励图像和梯度方向图像，从而可以得到二维WLD直方图。其中，N为图像的维度，T为方向域的分段个数，每一小块都对应一个差分激励和梯度方向。

　　为便于分类，，需要将二维直方图转化为一维直方图。整个过程如下图所示，其实我的理解就是，一行一行的排列，（就像在C里，二维数组其实是个一维数组一样，只是他是一行一行的读取罢了）

 

 

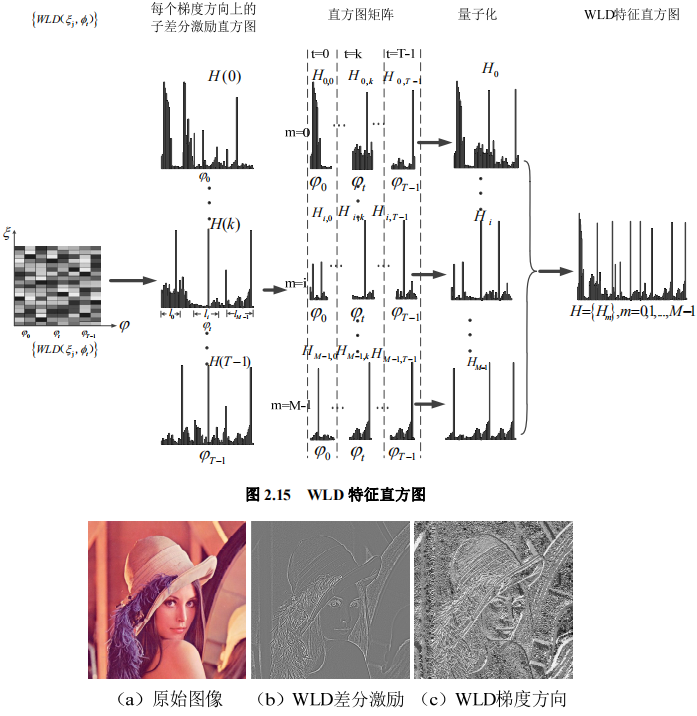
 　　综合：了解了这几个基本信息以后，我们来看一张图，好详细理解WLD算子：

　　对于差分激励来讲，v00，v01，我们知道他是可以看作上图中的滤波算子，同理，v10，v11也是如此。我们通过分别计算完差分激励与梯度方向后，得到有关二者的二维直方图，最后将二维直方图一维化，即为WLD算子的全部操作。

 二、代码及其结果

　　以下为WLD算子的代码：

image=imread('lena.jpg');
image=rgb2gray(image);
d_image=double(image);
[xsize ysize] = size(d_image);
EPSILON=0.0000001;
numNeighbors=8; d_differential_excitation = zeros(xsize-1,ysize-1);
d_gradient_orientation = zeros(xsize-1,ysize-1);%计算WLD
for x = 2:xsize-1for y = 2:ysize-1% 计算差励v00=d_image(x-1,y-1)+d_image(x,y-1)+d_image(x+1,y-1)+d_image(x-1,y)+d_image(x+1,y)+d_image(x-1,y+1)+d_image(x,y+1)+d_image(x+1,y+1)-8*d_image(x,y);v01=d_image(x,y);if ( v01 ~= 0 )d_differential_excitation(x,y)=atan(v00/v01);elsed_differential_excitation(x,y)=0;end% 计算梯度方向N2=d_image(x,y-1);         N6=d_image(x,y+1);N4=d_image(x+1,y);         N0=d_image(x-1,y);if ( abs(N0-N4) < EPSILON)		d_gradient_orientation(x,y) = 0;elsev10=N6-N2;		v11=N0-N4;d_gradient_orientation(x,y) = atan(v11/v10);% 映射至0-2pi之间%角度转化为数值 && 梯度方向的量化d_gradient_orientation(x,y)=d_gradient_orientation(x,y)*180/pi;if     (v11 >  EPSILON && v10 >  EPSILON)		d_gradient_orientation(x,y)= d_gradient_orientation(x,y)+ 180;   else if (v11 < -EPSILON && v10 >  EPSILON)      d_gradient_orientation(x,y)= d_gradient_orientation(x,y)+ 180;  else if (v11 < -EPSILON && v10 < -EPSILON)      d_gradient_orientation(x,y)= d_gradient_orientation(x,y); else if (v11 >  EPSILON && v10 < -EPSILON)		d_gradient_orientation(x,y)= d_gradient_orientation(x,y)+ 360; endendendendendend
end
% 对梯度方向值与差励进行量化
% 将差励6等分,梯度8等分
%reshape函数重新调整矩阵的行数、列数、维数。下为将所有元素展现为一列
d_differential_excitation_one = reshape(d_differential_excitation,[size(d_differential_excitation,1)*size(d_differential_excitation,2),1]);
d_gradient_orientation_one = reshape(d_gradient_orientation,[size(d_gradient_orientation,1)*size(d_gradient_orientation,2),1]);
% figure;
%直方图，指定柱状数量为6
H_dif = histogram(d_differential_excitation_one,6);
dif_edge=H_dif.BinEdges;
% figure;
H_gra = histogram(d_gradient_orientation_one,8);
gra_edge=H_gra.BinEdges;
% count 两个矩阵的像素点的直方图归到6*8矩阵 
%循环实现计数功能，即每一节直方图的出现的像素点的个数
histNumbers = zeros(6,8);
for i=1:length(d_differential_excitation_one)temp1 = d_differential_excitation_one(i);temp2 = d_gradient_orientation_one(i);for k = 2:length(dif_edge)if temp1 <= dif_edge(k)g1 = k-1;break;endendfor k = 2:length(gra_edge)if temp2 <= gra_edge(k)g2 = k-1;break;endendhistNumbers(g1,g2) = histNumbers(g1,g2)+1;
end%figure(111);%bar3(histNumbers');
mid_dif=[];%二维直方图的完善
for i=1:length(dif_edge)-1temp = (dif_edge(i)+dif_edge(i+1))/2;temp = round(temp*100)/100;mid_dif = [mid_dif,temp];
end
set(gca, 'XTickLabel',{num2str(mid_dif(1)),num2str(mid_dif(2)),num2str(mid_dif(3)),num2str(mid_dif(4)),num2str(mid_dif(5)),num2str(mid_dif(6))});
mid_gra=[];
for i=1:length(gra_edge)-1temp = (gra_edge(i)+gra_edge(i+1))/2;temp = round(temp*100)/100;temp = temp*2*pi/360;mid_gra = [mid_gra,temp];
endbarhang=[];
for i=1:size(histNumbers,1)barhang=[barhang,histNumbers(i,:)];
end
% bar(barhang);
% % 绘图
figure(123);
subplot(2,2,1),imshow(d_differential_excitation,[]); title('差励')
image_DE = (255* (d_differential_excitation - (-pi/2))/((pi/2)-(-pi/2)));
subplot(2,2,2),imshow(mat2gray(uint8(image_DE)));title('差励归到[0,255]')
subplot(2,2,3),imshow(d_gradient_orientation,[]); title('梯度方向')
image_DO = (255* (d_gradient_orientation - (-pi/2))/((pi/2)-(-pi/2)));
subplot(2,2,4),imshow(mat2gray(uint8(image_DO)));title('梯度方向归到[0,255]')

　　结果如下：

　　差分激励和梯度方向的两幅图像分别显示如下：

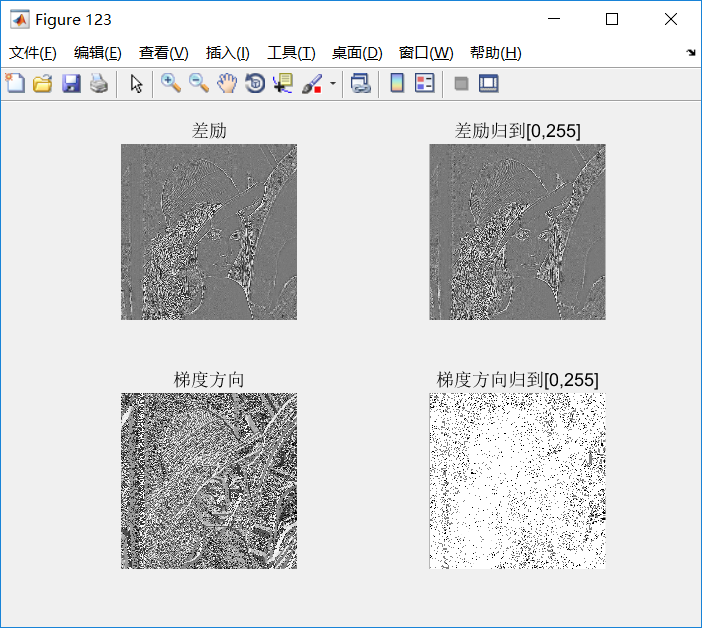
　　一维直方图效果为：

 

参考文献;

[1]李思.复杂光照下图像特征提取.（D）.西安：长安大学，2018.

 

2019-05-09

17:41:41

 

 

　　

转载于:https://www.cnblogs.com/lyxyhhxbk/p/10835780.html

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/387726.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Linux下Nagios的安装与配置

Linux下Nagios的安装与配置

Linux下Nagios的安装与配置 一、Nagios简介 Nagios是一款开源的电脑系统和网络监视工具&#xff0c;能有效监控Windows、Linux和Unix的主机状态&#xff0c;交换机路由器等网络设置&#xff0c;打印机等。在系统或服务状态异常时发出邮件或短信报警第一时间通知网站运维人员&am…
阅读更多...
POJ_3262 Protecting the Flowers 【贪心】

POJ_3262 Protecting the Flowers 【贪心】

一、题面 POJ3262 二、分析 这题要往贪心上面想应该还是很容易的&#xff0c;但问题是要证明为什么比值关系就能满足。 可以选择几个去分析&#xff0c;入1-6 与 2-15 和 1-6 与2-5 和 1-6 与 2- 12。 三、AC代码 1 #include <cstdio>2 #include <iostream>3 #in…
阅读更多...
WebLogic安装Linux centos7

WebLogic安装Linux centos7

一、安装前准备工作&#xff1a; 1、创建用户useradd weblogic;创建用户成功linux系统会自动创建一个和用户名相同的分组&#xff0c;并将该用户分到改组中。并会在/home路径下创建一个和用户名相同的路径&#xff0c;比如我们创建的weblogic。 注&#xff1a;当然&#xff0…
阅读更多...
jquery如何阻止子元素继承父元素的事件（又称事件冒泡）

jquery如何阻止子元素继承父元素的事件（又称事件冒泡）

非常简单&#xff0c;子元素上添加如下代码即可 1 $(a).click(function(e){ 2 e.stopPropagation(); 3 }); 老版本为event,现在用e就行 转载于:https://www.cnblogs.com/chengbo2130/p/10152747.html
阅读更多...
java spring cloud 版 b2b2c 社交电商-服务消费者（Feign）

java spring cloud 版 b2b2c 社交电商-服务消费者（Feign）

社交电商平台源码请加企鹅求求&#xff1a;一零三八七七四六二六。Feign是一个声明式的伪Http客户端&#xff0c;它使得写Http客户端变得更简单。使用Feign&#xff0c;只需要创建一个接口并注解。它具有可插拔的注解特性&#xff0c;可使用Feign 注解和JAX-RS注解。Feign支持可…
阅读更多...
Mybaits自定义SQL

Mybaits自定义SQL

最近有个同事要包装一个可以执行sql语句的功能用的是mybatis 最开始他想到的方案是拿到数据库连接再执行sql语句。 后来出了某些错误来问我&#xff0c;为了寻求比较快的解决方法于是我就试试了下下面的方法。 首先在Mapper添加 <select id"select" resultMap&qu…
阅读更多...
Beta 冲刺 （7/7）

Beta 冲刺 （7/7）

团队信息 队名&#xff1a;爸爸饿了组长博客&#xff1a;here作业博客&#xff1a;here组员情况 组员1&#xff08;组长&#xff09;&#xff1a;王彬 过去两天完成了哪些任务 协助完成安卓端的整合完成安卓端的美化协助制作宣传视频 接下来的计划 & 还剩下哪些任务 I am d…
阅读更多...
类的转换函数调用的优先级与是否用const修饰的关系

类的转换函数调用的优先级与是否用const修饰的关系

P415 C Primer Plus (第六版&#xff09;(待解决~~知道原理的同学请留言&#xff0c;多谢~~&#xff09; #include <iostream>using namespace std; class Cp{private: 　　int a; 　　double b;public: 　　Cp() 　　{ 　　　　a 1; 　　　　b 2.2; 　　} operator in…
阅读更多...
Java Web 学习与总结（一）Servlet基础

Java Web 学习与总结（一）Servlet基础

配置环境&#xff1a;https://www.cnblogs.com/qq965921539/p/9821374.html 简介&#xff1a; Servlet是Sun公司提供的一种实现动态网页的解决方案&#xff0c;在制定J2EE时引入它作为实现了基于Java语言的动态技术&#xff0c;目前流行的Web框架基本都基于Servlet技术&#xf…
阅读更多...
堪称经典

堪称经典

程序员作为高智商、高收入、高压力群体&#xff0c;经常会有各种自嘲&#xff0c;而且还天生携带段子手基因。不信看看下面这些段子&#xff0c;一般人哪能懂&#xff01; 1、杀一个程序员不需要用枪&#xff0c;改三次需求就可以了 2、程序员退休后决定练习书法&#xff0c;于…
阅读更多...
【洛谷 P1659】 [国家集训队]拉拉队排练（manacher）

【洛谷 P1659】 [国家集训队]拉拉队排练（manacher）

题目链接 马拉车简单膜你 #include <cstdio> #include <cstring> #include <algorithm> using namespace std; const int MAXN 11000010; const int MOD 19930726; char b[MAXN], a[MAXN << 1]; int hw[MAXN << 1], ans 1, n, c[MAXN]; #defi…
阅读更多...
Judy Beta 第三天

Judy Beta 第三天

概述 前端部分对于打包的流程以及相关 package.json 的配置都已经比较熟悉了&#xff0c;目前主要负责对新实现的 feature 做测试&#xff0c;以及参考 DAP 为后端明确数据交换的格式及参数内容等。 后端部分按照更新的 wiki 实现了变量展开&#xff0c;并且根据 DAP 的协议流程…
阅读更多...
oracle表空间不足

oracle表空间不足

oracle表空间不足&#xff0c;一般有两个原因&#xff1a;一&#xff0c;原表空间太小&#xff0c;没有自增长&#xff1b;二&#xff0c;表空间已自增长&#xff0c;而且表空间也已足够大&#xff0c;对于这两种原因分别有各自的解决办法。 【检查原因】 1、查看表在那个表空…
阅读更多...
python学习中遇到的问题

python学习中遇到的问题

2019独角兽企业重金招聘Python工程师标准>>> def contract_str():index 8db_size 8new_table_name b_str(index & (db_size-1))print new_table_name ImportError: No module named mysql.connector import mysql.connector as sql_connector Python保存时提…
阅读更多...
Arcgis 使用ArcToolbox实现数据统计

Arcgis 使用ArcToolbox实现数据统计

在ArcMap中打开ArcToolbox&#xff0c; ->Data Managerment Tools ->General ->Add你需要统计的所有数据转载于:https://www.cnblogs.com/CoffeeEddy/p/10161863.html
阅读更多...
oracle分区索引及循环插入

oracle分区索引及循环插入

表可以按range、hash、list分区&#xff0c;表分区后&#xff0c;其上的索引和普通表上的索引有所不同&#xff0c;oracle对于分区表上的索引分为2类&#xff0c;即局部索引和全局索引&#xff0c;下面分别对这2种索引的特点和局限性做个总结。 局部索引local index 1.局部索引…
阅读更多...
classloader.getresources() 介绍

classloader.getresources() 介绍

转载自&#xff1a; https://www.cnblogs.com/bhlsheji/p/4095699.html ◆普通情况下,我们都使用相对路径来获取资源,这种灵活性比較大. 比方当前类为com/bbebfe/Test.class 而图像资源比方sample.gif应该放置在com/bbebfe/sample.gif 而假设这些图像资源放置在icons文件夹下,则…
阅读更多...
Anti-Aliasing SSAA MSAA MLAA SRAA 简介

Anti-Aliasing SSAA MSAA MLAA SRAA 简介

http://blog.csdn.net/codeboycjy/article/details/6312758 前两天在浏览游民星空的时候&#xff0c;小编居然在文章中挂了一篇技术文章&#xff0c;是关于SRAA的。对于AA的了解很少&#xff0c;正好入职之前还有几天的空闲时间&#xff0c;所以就这个机会把AA的一些基本算法简…
阅读更多...
MyBatis多数据源配置(读写分离)

MyBatis多数据源配置(读写分离)

MyBatis多数据源配置(读写分离) 首先说明&#xff0c;本文的配置使用的最直接的方式&#xff0c;实际用起来可能会很麻烦。 实际应用中可能存在多种结合的情况&#xff0c;你可以理解本文的含义&#xff0c;不要死板的使用。 多数据源的可能情况 1.主从 通常是MySQL一主多…
阅读更多...
UI简单工作

UI简单工作

UI用户界面 需求——效果图——风格设计——高保证效果——html 网页的宽度屏幕的宽度-纵向滚动条的宽度 企业网站一般是1280 根据百度流量研究所 目前我们的网页注主要是1024和1200 这样的宽度符合大体市场 首屏高度。 首屏的概念来源于出版领域 报纸折叠后贩卖&…
阅读更多...
最新文章

Copyright @ 2022~2023