Anti-Aliasing SSAA MSAA MLAA SRAA 简介

http://blog.csdn.net/codeboycjy/article/details/6312758

前两天在浏览游民星空的时候，小编居然在文章中挂了一篇技术文章，是关于SRAA的。对于AA的了解很少，正好入职之前还有几天的空闲时间，所以就这个机会把AA的一些基本算法简单学习了一下，不过也只是学习到了一点皮毛而已。
本文将简单介绍四种反走样算法，他们分别是：
SSAA: Super Sampling Anti-Aliasing
MSAA: Multi Sampling Anti-Aliasing
MLAA: Morphological Anti-Aliasing
SRAA: Sub-pixel Reconstruction Anti-Aliasing
当然，AA算法的种类实在是很多，还有CSAA，ADAA，Transparent AA等等。本文就简单介绍上面四种吧。
首先，什么是走样呢？我们在现实生活中观察到的物体经常是细节非常丰富的，而大部分信息的频率远远高于人眼的识别能力。而计算机中的图像是由一个一个离散的pixel组成的，其实是个有限的集合。所以它只能用来逼近现实中的场景，并不能完美的重现。走样有很多表现形式，例如边缘的锯齿，采样频率过低等。本文的AA算法都是针对锯齿边缘的。一般而言，纹理的采样频率过低都是通过AF或者更复杂的采样算法来解决的。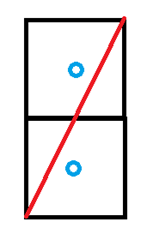

举个简单的例子，我们放大一条直线所经过的两个pixel。由于对于每个像素，我们只在像素的中心采样，所以对于上图而言，上面的像素中的采样点是在直线上面的，而下面采样点则在直线的下面。假设我们要把直线下面的图像填充成黑色，如果没有AA，那么下面的像素就会是纯黑色，而上面是纯白色。而这种情况会产生三角形边缘的锯齿现象，我们称之为走样。下图为经过MLAA处理前后的图像变化。

当然，如果屏幕分辨率的细致程度已经超过了人眼的识别能力的话，例如iphone4的retina屏幕，那么由于几何体边缘带来的走样现象也会基本没什么影响了。不过大部分的显示器还是能用肉眼观察到锯齿的。
首先我们了解下SSAA的算法吧。几何体的边缘在理论上来说是无限细致的，因为是用数学公式表达的。所以如果投影到光栅屏幕上的话，无论如何都会有细节损失的，只不过是不是明显罢了。当屏幕分辨率增加或者屏幕分辨率不变，而每个像素的采样点增多的时候，这种细节会更好的表现在用户面前，所以解决AA的一个最直观的办法就是通过增加分辨率。如果在图像的长度和宽度都增加2倍的条件下（4 X SSAA )，再次渲染图像。然后做一个downfiltering，那么图像的细节会表现的更好一些，锯齿会明显的减少。这种办法就是SSAA了，挺Brute Force的办法。这种方法的好处在于可以更完美的表现画面，不过问题在于其计算代价是与屏幕分辨率成正比的。4 x SSAA 的速度要比没有AA慢4倍左右的时间，对于大多数应用来说，是得不偿失的。从性能角度而言，SSAA是不实际的。
当然，即使确定了SSAA算法后，也还有一些其他的细节需要考虑。例如，16 x SSAA可以被理解为每个像素有十六个采样点，而采样点的分布是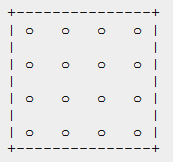

而这种分布对于反走样并不是特别有效的，可以采用如下几种分布来替换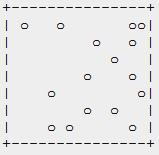

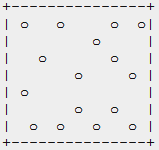
从左到右依次是随机分布，泊松分布和Jittered分布。随即分布的问题在于采样点数量不多的时候，算法的结果不是特别稳定。泊松分布的问题在于并不能轻易计算出泊松分布的位置，而且位置计算代价很大。当然还有很多其他的分布，这里就不多介绍了。不同的采样点分布算法可以不同程度的改变反走样的效果。
由于SSAA的算法代价过于大，所以应用价值相对而言较小。MSAA假设一个像素内的颜色变化是不大的，从而有效的把颜色和顶点的位置，法线等信息分离开来了。这种算法在很早的Geforce3中，有硬件实现。由于在当时的硬件条件下，纹理的读取的开销很大，所以把这部分独立出来就充分的节省了bandwidth与fillrate。假设这里是4 x MSAA，每个像素的四个采样点中，除了没有颜色信息，会有其他位置等信息。注意这里面的深度信息也是存储在每个采样点中的，就是说深度比较也是基于sub-pixel级别的。Geforce 4系列的AA没有本质的变化，不过在采样点的分布上做了一些调整。

蓝色的为像素的中心，而红色的为4 x MSAA的实际采样点。由于平均距离小了很多，所以反走样的效果有了一定的提升。而同期的AMD的硬件的AA效果要好一些，主要是采样分布的原因。Geforce 4用的采样分布属于ordered grid sampling，而AMD采用了另一种rotated grid sampling。

从反走样的质量而言，AMD的R300系列要远远领先与Nv30。
随着游戏产业的不断发展，游戏场景也更加的复杂。很多游戏中利用alpha test简化场景的复杂度。例如下面的铁丝网：

问题就出现了，由于MSAA的纹理采样频率依旧和没有AA的时候一样，所以对于上图左边而言，没有MSAA和经过MSAA处理的效果基本没有区别。因为上面的铁丝网是通过alpha test来模拟的，而没有实际的网格。MSAA的纹理采样率导致了其在这种情况下的无能为力。当然后来就有了adaptive AA来改进这种问题。
上述的MSAA算法还有一个很严重的问题，就是他们只能与forward rendering结合。而随着游戏中光源效果的复杂，deferred rendering越来越受到关注。而无论是defered rendering还是msaa都是通过把颜色的计算与几何体计算分离开来，而两者是不能并存的。这就导致了很多麻烦。从某种程度上，MLAA和SRAA可以理解为后处理运算，所以是可以和deferred rendering结合的。
MLAA更像是一种图像处理方法，它不需要任何前验信息，只根据像素的颜色进行处理。它可以和raster、ray tracing或者其他算法结合，而且完全不需要生成任何多余的信息。MLAA的算法相对来说复杂很多，这里就不介绍了。
不过由于MLAA只是根据颜色进行判定，所以很多时候可以影响一些高频纹理。当然这些纹理很可能在AF采样后，自动适应MLAA算法了。至少该算法的作者称MLAA不会对纹理的采样其反作用。
MLAA的算法速度可能相对慢一些，作者的数据是在一个单核3GHz的处理器下，每秒可以处理20M的像素。对于大分辨率而言，这个速度可能还不能算是实时。如果利用GPU或者larrabee，可能速度会有些提升吧。论文中是在ray tracing的渲染方法下实验的，由于对于动态场景的ray tracing需要更新空间划分结构，所以可以利用空余线程处理图像，基本不会带来什么开销。对于实时渲染可能就需要用其他手段了。
由于MLAA的一些限制，SRAA就提出了解决方案。SRAA虽然也相当于后处理，不需要任何forward rendering的元素。不过SRAA需要一个G buffer，这个G buffer的分辨率一般要大一些，这里就假设是4 x SRAA吧，那么G Buffer就是back buffer分辨率的4倍。SRAA根据G Buffer中的几何信息，把每个像素与周围一定范围的像素进行混合。由于引入了几何信息，所以可以避免很多MLAA的错误。

我们可以看到(c)图中的MLAA算法把右下角本来清晰的矩形模糊化了，而SRAA由于引入了几何信息，很好的保持了其清晰的特性，而又模糊了上面的锯齿。
SRAA算法可以在保持算法性能的条件下生成与16 x SSAA相媲美的画面，当然有些细节可能还是要差一点。毕竟有些情况下，其算法中的部分假设是不成立的。
基本就介绍到这里吧，没有怎么细致介绍，只是概要的提到了一些算法而已。