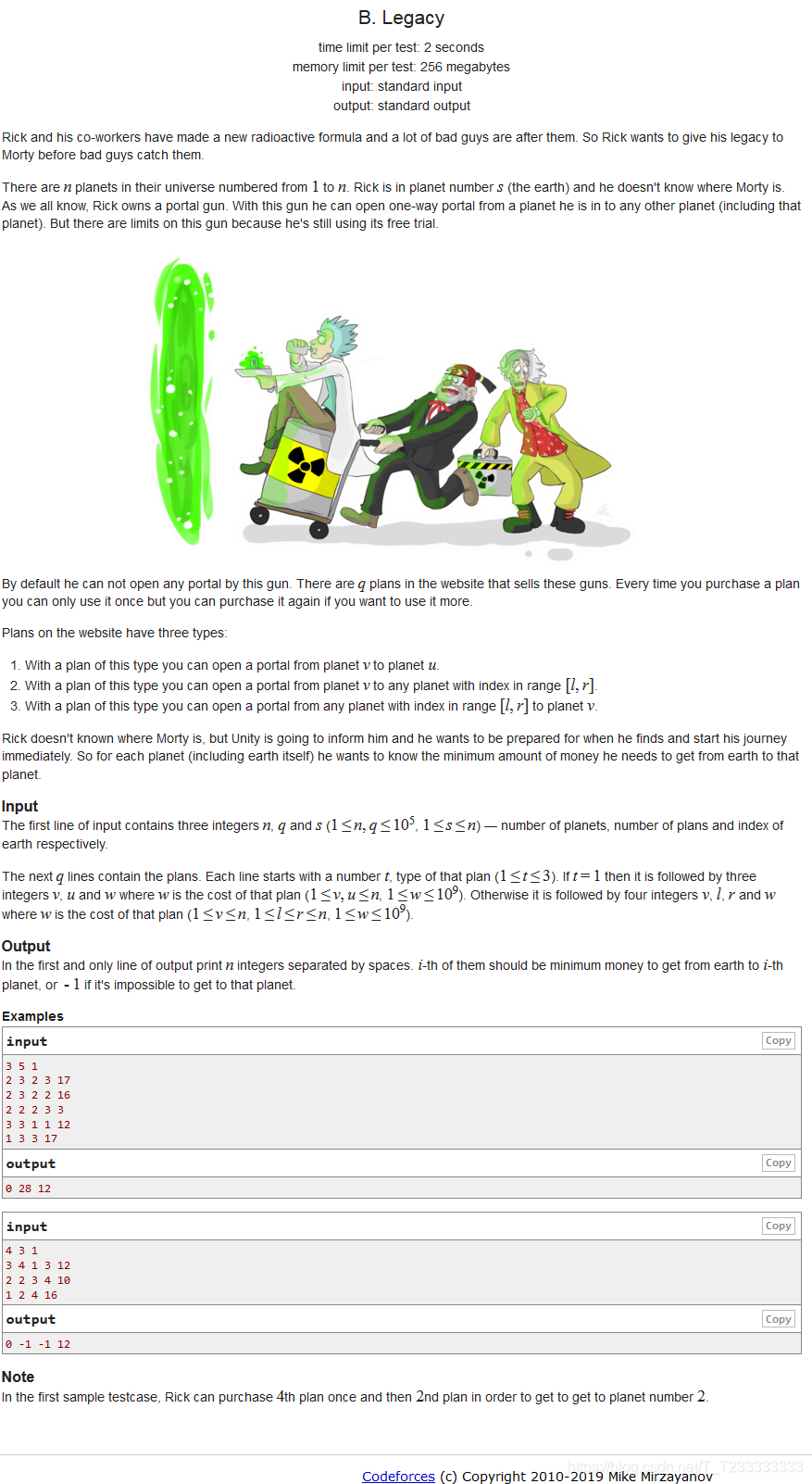
【题目描述】
CodeForces - 786BLegacy
【题目分析】
题目大概意思就是有三种操作:
- 从某个点到另一个点
- 从某个点到另一个区间
- 从某个区间到另一个点
然后询问从其中一个点到其他所有点的距离——这很显然是一个求单源最短路径的。我们简单的想法显然是建一个图,每次操作就进行暴力连边,反正也没有修改。可是复杂度不允许。
我们再观察一下操作:对区间的操作,这让我们不由得想起了线段树,毕竟线段树可是区间神器,可是就算用了线段树,我们能做些什么呢?
线段树是保存区间信息的数据结构,我们对于从点到区间的关系,不妨修改为从点到线段树节点的关系,然后再使线段树节点和他们的叶子节点之间本来就带有一条路径,那么从一个点到另一个区间的关系就这样被简化为从一个点到几个点的关系,可以有效降低复杂度。
具体做法就是在建树的过程中就让每个线段树节点和他们的叶子节点之间含有一条权值为0的有向边。
之所以是有向边是因为从点到区间的关系有两种,我们得建立两种线段树,分别是从父节点指向叶子节点和从叶子结点指向根节点,对应的是从点到区间和从区间到点的关系。而且两个线段树的叶子节点,也就是最下面的节点指向的都是原来区间的节点,这样就在原来的区间上建立了从点到区间再从区间到点的关系。详细情况可以看一下另一位大佬博主的图
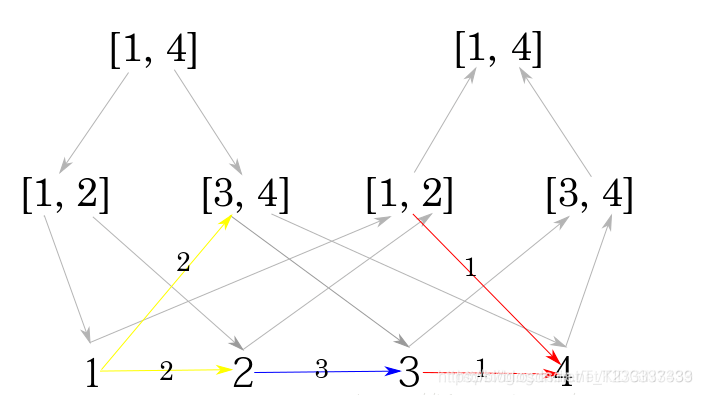
这个图是进行了三个操作:
1 2 3 3 节点2到节点3有一条权值为3的边(蓝色)
2 1 2 4 2 节点1到区间[2,4]有权值为2的边(黄色)
3 4 1 3 1 区间[1,3]到节点4有权值为1的边(红色)
再在这张图上跑最短路(因为有0边,最好还是用SPFA)
【AC代码】
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<vector>
#include<queue>
#include<set>
#include<climits>
#include<cstdlib>
#include<cmath>using namespace std;typedef long long ll;const int MAXN=100005;
const ll INF=0x3f3f3f3f3f3f3f3f;
int head[MAXN<<2],ls[MAXN<<2],rs[MAXN<<2];
int root1,root2,tot,cnt;
struct edge
{int v,w,next;
}edge[MAXN*20];
ll dis[MAXN<<2];
queue<int> q;inline void AddEdge(int u,int v,int w)
{edge[++tot].v=v; edge[tot].w=w; edge[tot].next=head[u]; head[u]=tot;
}void build1(int &k,int l,int r)
{if(l==r){k=l; return;}k=++cnt;int mid=(l+r)>>1;build1(ls[k],l,mid); build1(rs[k],mid+1,r);AddEdge(k,ls[k],0); AddEdge(k,rs[k],0);
}void build2(int &k,int l,int r)
{if(l==r){k=l; return;}k=++cnt;int mid=(l+r)>>1;build2(ls[k],l,mid); build2(rs[k],mid+1,r);AddEdge(ls[k],k,0); AddEdge(rs[k],k,0);
}void update1(int k,int l,int r,int x,int L,int R,int w)
{if(l>=L && r<=R){AddEdge(x,k,w);return;}int mid=(l+r)>>1;if(L<=mid) update1(ls[k],l,mid,x,L,R,w);if(R>mid) update1(rs[k],mid+1,r,x,L,R,w);
}void update2(int k,int l,int r,int x,int L,int R,int w)
{if(l>=L && r<=R){AddEdge(k,x,w);return;}int mid=(l+r)>>1;if(L<=mid) update2(ls[k],l,mid,x,L,R,w);if(R>mid) update2(rs[k],mid+1,r,x,L,R,w);
}void SPFA(int s)
{memset(dis,0x3f,sizeof(dis));dis[s]=0; q.push(s);while(!q.empty()){int u=q.front(); q.pop();for(int i=head[u];i;i=edge[i].next){int v=edge[i].v,w=edge[i].w;if (dis[u]+w<dis[v]) dis[v]=dis[u]+w,q.push(v);}}
}int main()
{int n,m,s;int cmd,l,r,v,w,u;scanf("%d%d%d",&n,&m,&s);cnt=n; tot=0;build1(root1,1,n); build2(root2,1,n);for(int i=0;i<m;i++){scanf("%d",&cmd);if(cmd==1){scanf("%d%d%d",&u,&v,&w);AddEdge(u,v,w);}else{scanf("%d%d%d%d",&v,&l,&r,&w);if(cmd==2)update1(root1,1,n,v,l,r,w);elseupdate2(root2,1,n,v,l,r,w);}}SPFA(s);for(int i=1;i<=n;i++){cout<<(dis[i]<INF?dis[i]:-1)<<" ";}return 0;
}









)









