人的大脑神经网络的复杂程度有人说，只有银河系可以比拟。总所周知，神经网络就是模仿大脑神经网络用数学知识构造的模型。单个神经元还是比较简单的。

神经元

一个神经元有树突，轴突，和细胞体等部分。树突接受输入信息，细胞核处理信息，轴突传出处理后的信息。

由神经元细胞，抽象出了它的数学模型如图：

像这种神经元就叫感知器，也叫感知机。感知机是一类人造神经元，在许多神经网络中，主要的神经元模型是sigmoid神经元。

感知机通过二进制输入X的矩阵，产生一个二进制的输出。每个X代表一个属性，然后w也叫权重，权重值的大小代表每个属性的重要程度，或者对结果的影响程度。

神经元的输出，要么是0要么是1，由权重和∑jwjxj∑jwjxj的值是否小于或者大于某一阈值。和权重一样，阈值(threshold)也是一个实数，它是神经元的一个参数。

我们简化一下，用W·X代替∑jwjxj ,其中W和X分别是权重值和输入值所组成的向量。其次，我们可以把阈值threshold移到不等式的另一边，用b代替−thresholdb，其中b被称为感知机的偏差。得到：

下面是一个更多层次的感知机，可以感知更复杂的输入。

Sigmoid神经元

当我们拿着感知机去学习解决一些问题时，举个例子，比如我们要识别猫，和老虎，我们知道小猫，和小老虎是挺像的，不像区别猫和狗那样简单，我们想办法对网络的权重和偏差做一些小的改变，使得网络可以区分猫和狗。一次又一次调整权重和偏差，使得输出越来越好，网络就得到了学习。理论很美好，现实确很残酷。事实上，任何一个感知机上发生一点小的改变有时可能导致感知机的结果翻转(要么翻转要么不变)，由0变为1或者相反。这样的翻转可能造成其他所有感知机的复杂变化。所以操作十分困难。

于是升级版的神经元诞生了——sigmoid神经元。sigmoid神经元和感知机非常相似，但是它的输入向量不在局限于0和1，而是0到1之间的连续值。

sigmoid神经元对每个输入都有分配权重和一个总的偏差。但是输出也不再是0和1，而是σ(w⋅x)+b，其中σ被称为sigmoid函数，定义为：

一个拥有输入x1,x2...权重w1,w2...偏差b的sigmoid神经元的输出为：

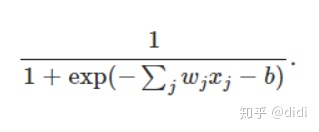
说当z=w⋅x+b是一个很大的正数时，sigmoid神经元的输出就接近于1，这就像一个感知机一样。反之当z=w⋅x+b是一个很小的负数时，sigmoid的输出结果趋近于0，这和感知机的行为很相似。只有当w⋅x+b的值不大不小的时候，sigmoid的输出才和感知机不一样。如图：

可以看出，sigmoid函数是一条平滑曲线，而感应机应该是这样的：

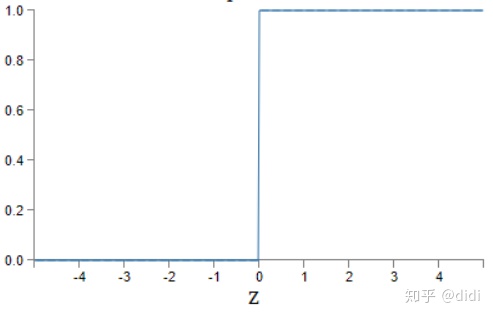
这就是激活函数的效果，通过计算发现，使用σ这样一个指数函数对于分化是有好处的。σ函数是最常见的激活函数。感知机和sigmoid神经元之间最大的不同在于，sigmoid输出的值不止0和1.他们可以输出0到1之间的所有实数。

神经网络结构

神经网络结构就是上述神经的升级版。最左边一层叫输入层，这一层有输入神经元，中间两层为隐藏层，最后为输出层，有输出神经元。

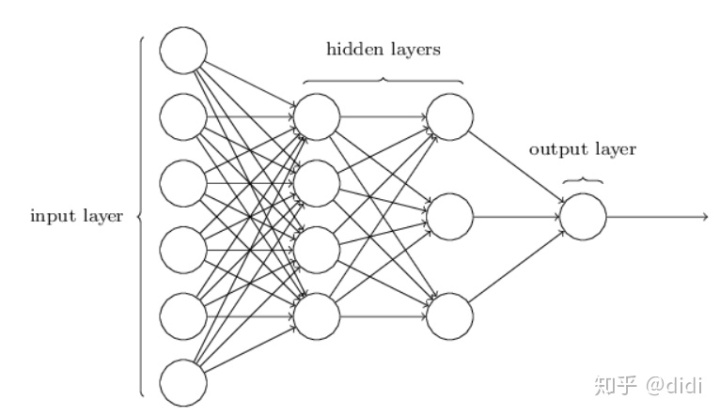
这样的多层网络有时候被称作多层感知机（MLPs），尽管这个网络是有sigmoid组成的而不是感知机。

我们所讨论的神经网络都是上一层的输出作为下一层的输入。也就是前反馈神经网络，信息总是往前走的，不会反向。在这个是函数σ作为激活函数时，没有环形的神经网络。这样的神经网络也叫前馈神经网络。

而递归神经网络是可能存在返馈回路的。它让神经元在有限时间里激活，然后保持非激活状态。这种激活可以刺激其他神经元在稍后一段时间激活。

递归神经网络的热度比前馈神经网络的小，有一部分原因递归网络的学习算法目前不那么强大。个人感觉它比前馈神经网络复杂一些。