多叉树的前序遍历_二叉树的非递归遍历的思考

封面图来自wikipedia

1 简介

二叉树的深度优先遍历（前序遍历、中序遍历、后序遍历）是一个比较基本的操作。如果使用递归的做法，很容易写出相应的程序；而如果使用非递归的做法，虽然也能写出相应的代码，但是由于三种非递归的遍历没有统一的格式，比较难记住。在这里，介绍一种统一格式的非递归写法。

2 递归做法

先介绍一下二叉树的三个深度优先遍历的基本概念：

前序遍历：先访问根节点，然后前序遍历左子树，最后前序遍历右子树。
中序遍历：先中序遍历左子树，然后访问根节点，最后中序遍历右子树。
后序遍历：先后序遍历左子树，然后后序遍历右子树，最后访问根节点。

根据概念很容易写出对应的递归遍历代码

2.0 数据结构定义

struct TreeNode{TreeNode* left;TreeNode* right;int val;
};

2.1 前序遍历

vector<int> preorder(TreeNode* root, vector<int>& res) {if (!root) return res;res.push_back(root->val);preorder(root->left, res);preorder(root->right, res);return res;
}

2.2 中序遍历

vector<int> inorder(TreeNode* root, vector<int>& res) {if (!root) return res;inorder(root->left, res);res.push_back(root->val);inorder(root->right, res);return res;
}

2.3 后序遍历

vector<int> postorder(TreeNode* root, vector<int>& res) {if (!root) return res;postorder(root->left, res);postorder(root->right, res);res.push_back(root->val);return res;
}

3 非递归做法

先列出代码，后面再写下代码的思想以及自己的理解。

可以看出三种遍历的写法，除了三句执行入栈的代码，顺序不一样，其他都是一致的，实现了格式的统一。

3.1 前序遍历

void preorder(TreeNode *root, vector<int>& res)
{stack< pair<TreeNode*, bool> > s;s.push(make_pair(root, false));bool visited;while(!s.empty()) {root = s.top().first;visited = s.top().second;s.pop();if(root == NULL) {continue;}if(visited) {res.push_back(root->val);} else {s.push(make_pair(root->right, false));s.push(make_pair(root->left, false));s.push(make_pair(root, true));}}
}

3.2 中序遍历

void inorder(TreeNode *root, vector<int>& res)
{stack< pair<TreeNode*, bool> > s;s.push(make_pair(root, false));bool visited;while(!s.empty()) {root = s.top().first;visited = s.top().second;s.pop();if(root == NULL) {continue;}if(visited) {res.push_back(root->val);} else {s.push(make_pair(root->right, false));s.push(make_pair(root, true));s.push(make_pair(root->left, false));}}
}

3.3 后序遍历

void postorder(TreeNode *root, vector<int>& res)
{stack< pair<TreeNode*, bool> > s;s.push(make_pair(root, false));bool visited;while(!s.empty()) {root = s.top().first;visited = s.top().second;s.pop();if(root == NULL) {continue;}if(visited) {res.push_back(root->val);} else {s.push(make_pair(root, true));s.push(make_pair(root->right, false));s.push(make_pair(root->left, false));}}
}

4 算法思想

4.1 简要说明

下面以前序遍历为例子，简单说说我自己的理解。先总结下自己的理解：

前序遍历的规则：“根节点-左子树递归-右子树递归”，等价于下面两个规则

对于每个节点，访问顺序为：“节点-左节点-右节点”
对于每个节点，左子树的节点全部访问完，再开始访问右子树的节点。

4.2 详细解释

接下来尝试对上面的话解释一下。

回看前序遍历的概念，可以发现它制定了遍历的规则：先是根节点，然后递归遍历左子树，最后递归遍历右子树，我们表示成“根节点-左子树-右子树”。这个好像不太直观，我们想想这个规则能不能表示成其他等价规则。首先想到的一点是：

(a) 对于树中的每一个节点，它以及它的两个子节点的访问顺序必须是 “节点-左子节点-右子节点”。

这个很容易理解。对于一个节点来说，它的左子节点是左子树的根节点，右子节点是右子树的根节点，既然要求 “节点-左子树-右子树”，那么必要条件就有 “节点-左子节点-右子节点”。其次，递归遍历使得对于每个节点，都有这样的要求。

但是这个只是必要条件，并不能唯一确定节点访问顺序。举个例子，假设有下面一棵二叉树，那么它的前序遍历是 “1-2-4-5-3-6-7”。假设我们只是规定了 “节点-左子节点-右子节点” 这个规则，那么我们便规定了下面三个序列的次序：“1-2-3”、“2-4-5”、“3-6-7”，（即：3 必须在 2 之后访问，2 必须在 1 之后访问...）然而我们没有规定这三个序列之间的相对次序，那么符合条件的次序就有很多了，比如 “1-2-3-4-5-6-7”、“1-2-3-6-7-4-5”，“1-2-4-3-6-5-7” 等等。

图1 - 二叉树例子

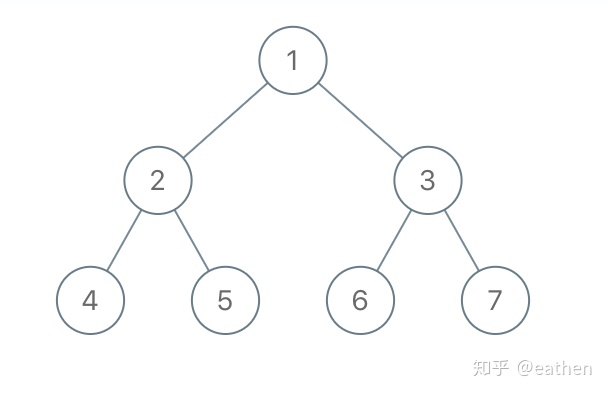
仔细思考了一下，出现上面这些序列的原因是：我们没有规定左子树 “2-4-5” 与右子树 “3-6-7” 两个子树之间的相对顺序。比如第一个例子 “1-2-3-4-5-6-7”，在左子树只访问根节点 “2” 之后，就去访问右子树的根节点 “3”，之后再访问左子树剩下的部分，最后再访问右子树剩下的部分。

我们知道正确的做法是：先访问完所有左子树的节点，再访问所有右子树的节点。于是得到第二条规则：

(b) 对于树中的每一个节点，只有当左子树的节点全部访问完，才能访问右子树的节点。

有了上述两条规则，遍历顺序便被唯一确定了。当然我不知道怎么严谨地证明这个结论。

回头再思考一下上面两个规则，第一个规则规定了节点与它的两个子节点（子树）之间的顺序，而第二个规则规定了两个子树之间的顺序。

5 代码对算法的实现

来看看代码怎么实现我们上面说的两点规则的。为了方便，我把代码搬了下来。

// 前序遍历
void preorder(TreeNode *root, vector<int>& res)
{stack< pair<TreeNode*, bool> > s;s.push(make_pair(root, false));bool visited;while(!s.empty()) {root = s.top().first;visited = s.top().second;s.pop();if(root == NULL) {continue;}if(visited) {res.push_back(root->val);} else {s.push(make_pair(root->right, false));s.push(make_pair(root->left, false));s.push(make_pair(root, true));}}
}

(1) 首先注意到，代码使用了栈，在元素入栈的时候，三条语句确定了一个节点与它的两个子节点之间的顺序。对所有的节点进行这个操作，便实现了规则(a)。
(2) 由于栈的 “后进先出” 特性，根据入栈的顺序，相比左子节点，右子节点会在栈更深的位置，所以后续会先访问左子节点。访问左子节点的时候，会将它的子节点压入栈，因此所有的左子树的节点都会比原本右子节点更先访问到。因此，栈的本身结构保证了所有的节点都执行了规则(b)。
(3) 代码中对每个节点使用了一个标记位，开始第一次入栈时，都标记为 false，只有当第二次入栈时，节点以及它的子节点顺序确定，才被标记成 true。换句话说，false 表示了当前节点与其子节点的顺序还没确定下来，true 表示当前节点与其子节点的顺序已经确定下来，因此可以被访问了。这个保证了树中的 “所有” 节点都执行了规则 (a)。

下面是算法执行的示意图，便于大家理解算法流程。