众所周知，softmax+cross entropy是在线性模型、神经网络等模型中解决分类问题的通用方案，但是为什么选择这种方案呢？它相对于其他方案有什么优势？笔者一直也困惑不解，最近浏览了一些资料，有一些小小心得，希望大家指正~

损失函数：交叉熵Cross Entropy

我们可以从三个角度来理解cross entropy的物理意义

从实例上直观理解

我们首先来看Cross Entropy 的公式：

假设存在两个分布

和

，

为样本的真实分布，

为模型预测出的样本分布，则在给定的样本集

上，交叉熵的计算方式为

通常情况下在线性模型、神经网络等模型中，关于样本的真实分布可以用one-hot的编码来表示，比如男、女分别可以用[0,1]和[1,0]来表示，同样的，C种类别的样本可以用长度为C的向量来表示，且一个样本的表示向量中有且仅有一个维度为1，其余为0。那会造成什么后果呢？我们来看一个例子，假设一个样本的真实label为

，预测的分布为

，则交叉熵为：

如果预测分布为

,则交叉熵为：

可以看出其实

只要label中1所对应下标的预测值越接近1，则损失函数越小，这在直观上就是符合我们对于损失函数的预期。

交叉熵为什么比均方误差好

作为回归问题的常见损失函数，均方误差公式为

，好像也可以用来计算分类问题的损失函数，那它为什么不适合分类问题呢？我们再来看一个例子假设一个样本的真实label为[0,0,0,1,0]，预测的分布为

,预测分布

,此时

,也就是说对于

而言，

似然估计的视角

我们知道，对于一个多分类问题，给定样本

,它的似然函数可以表示为

其中

是模型预测的概率，

是对应类的label，

为类别的个数，那么其

,

对应于

，

对应于

，其实

KL散度视角

KL散度又被称为相对熵，可以用来衡量两个分布之间的距离，想了解KL散度可以参考如何理解K-L散度。需要了解的是：KL散度越小，两个分布越相近。这么看KL散度是不是很符合我们对于两个分布损失函数的定义呢?

KL散度的公式为：

其中

为

的熵，注意这里的

是样本的真实分布，所以

为常数，因此，KL散度与交叉熵事实上是等价的，所以

softmax+cross entropy到底学到了什么？

我们知道在回归问题中的最常用的损失函数是均方误差

，那么在反向传播时,

,即

假定分类问题的最后一个隐藏层和输出层如下图所示

为最后一个隐藏层的C个类别,

为输出层，则有

，

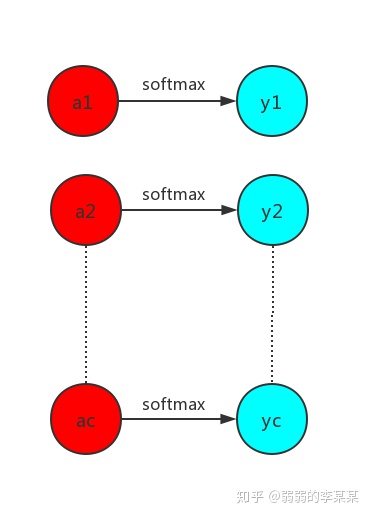
图中

，我们用

表示分母

，则

。

与所有的

都相关，因此需要用链式法则求导

下面求

，

的求导分为两种情况

当

时,

当

时，

代入上式得

注意这里

为所有label的和，应该等于1。