目录:
- 代码:
- 分析:
- 汇编:
代码:
main.c
#include <stdio.h>/*
程序描述:输出N*N中符合左右对角线与上下左右方向都没被使用的位置在每一行的所有情况使用检测左上角,正上角,右上角 三个方向有没有被使用来判断该行该位置是否可以使用当检测行大于N时,表示完成一种情况,按下回车键。从大于N行的这次find函数调用出栈。返回调用(使用大于N行的参数调用了find函数的)处。就是N行调用find函数的地方执行将N行原本选用好的位置重置,再找下一个。如果找到就重复上面大于N行的find函数调用如果没找到,将调用N行的find函数出栈,返回到N-1行调用find函数的地方,在N-1行查找找到就再调用回N行,找不到就再出栈,返回上一行也就是调用处。总结:在本行找到就调用到下一行查找,本行找不到就返回到上一行查找,找到就再返回到下一行,找不到就再返回到上一行,实现将所有情况输出*/
#define N 5typedef struct _tag_Pos
{int ios;int jos;
} Pos;static char board[N+2][N+2];//定义二维数组,加2用于上下左右四边
static Pos pos[] = { {-1, -1}, {-1, 0}, {-1, 1} }; //定义用于向左上角,正上角,右上角的位置递增的数组
static int count = 0;void init()//初始化数组函数
{int i = 0;int j = 0;for(i=0; i<N+2; i++)//将二维数组的四边赋上'#'{board[0][i] = '#'; //上board[N+1][i] = '#'; //下board[i][0] = '#'; //左board[i][N+1] = '#'; //右}for(i=1; i<=N; i++)//将内部内容赋上空格{for(j=1; j<=N; j++){board[i][j] = ' ';}}
}void display()//将整个二维数组输出显示函数
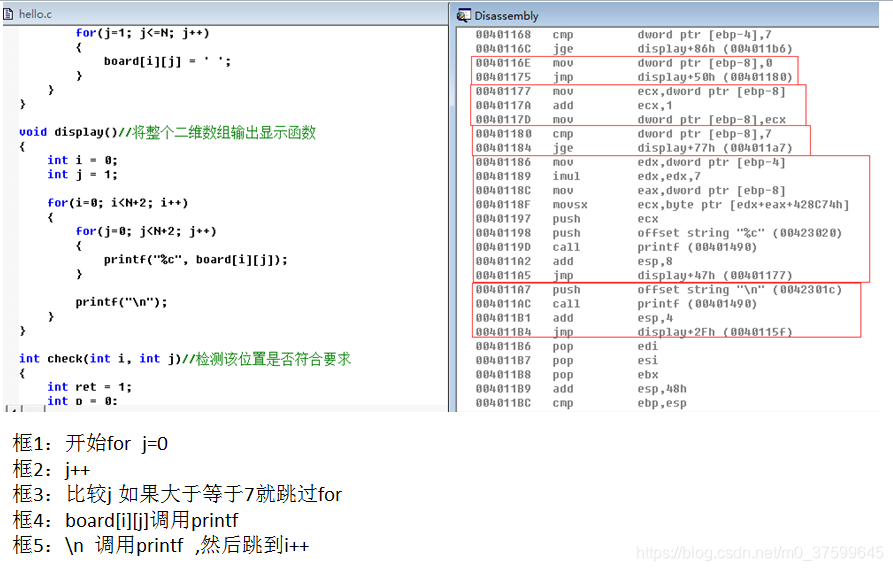
{int i = 0;int j = 1;for(i=0; i<N+2; i++){for(j=0; j<N+2; j++){printf("%c", board[i][j]);}printf("\n");}
}int check(int i, int j)//检测该位置是否符合要求
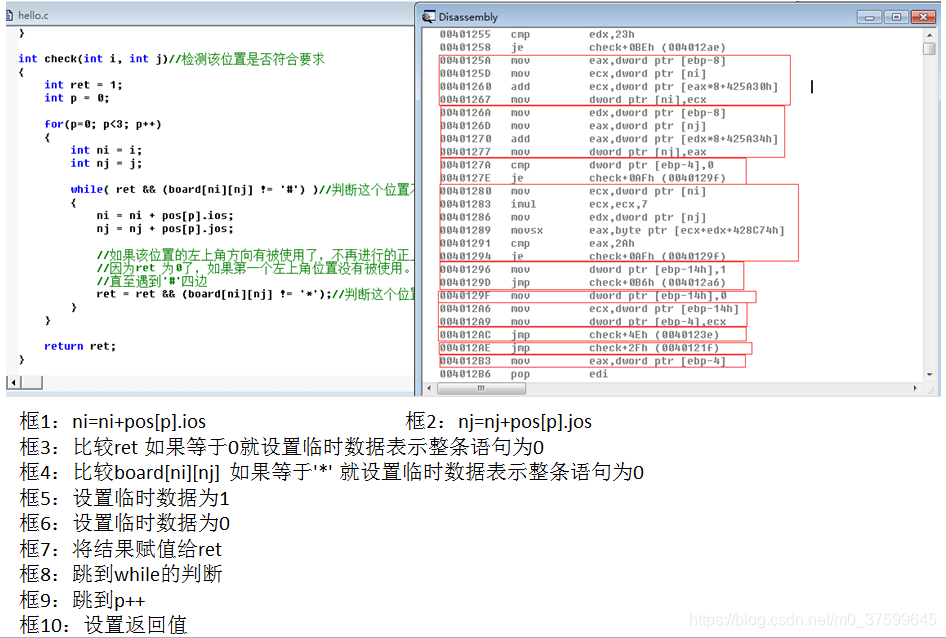
{int ret = 1;int p = 0;for(p=0; p<3; p++){int ni = i;int nj = j;while( ret && (board[ni][nj] != '#') )//判断这个位置不是在四边{ni = ni + pos[p].ios;nj = nj + pos[p].jos;//如果该位置的左上角方向有被使用了,不再进行的正上角与右上角的检测//因为ret 为0了,如果第一个左上角位置没有被使用。将一直位移比较//直至遇到'#'四边ret = ret && (board[ni][nj] != '*');//判断这个位置没被使用}}return ret;
}void find(int i)//查找位置函数(主要函数)
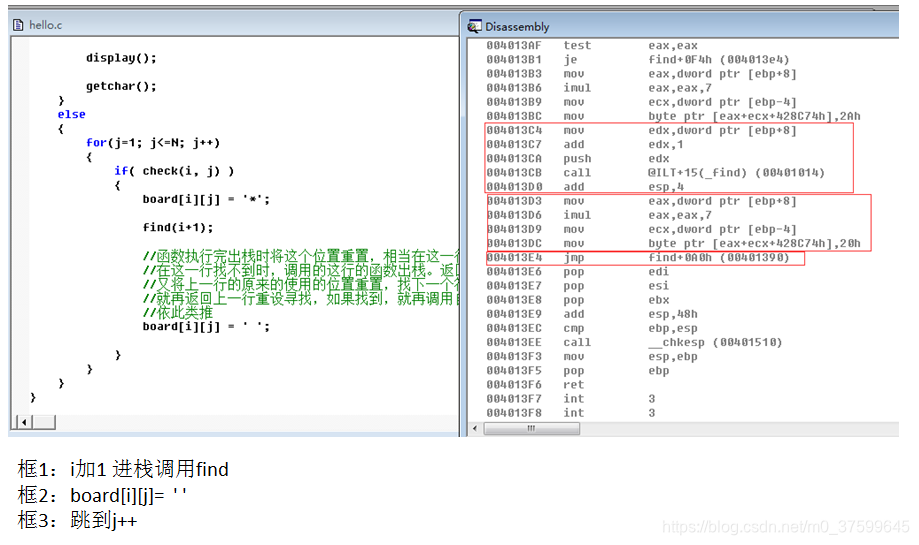
{int j = 0;if( i > N ){count++;printf("Solution: %d\n", count);display();getchar();}else{for(j=1; j<=N; j++){if( check(i, j) ){board[i][j] = '*';find(i+1);//函数执行完出栈时将这个位置重置,相当在这一行重新找下一个符合要求的位置//在这一行找不到时,调用的这行的函数出栈。返回到上一行调用的这个位置//又将上一行的原来的使用的位置重置,找下一个符合要求的位置,如果找不到//就再返回上一行重设寻找,如果找到,就再调用自身从新到下一行找,//依此类推board[i][j] = ' ';}}}
}int main()
{init();find(1);return 0;
}分析:
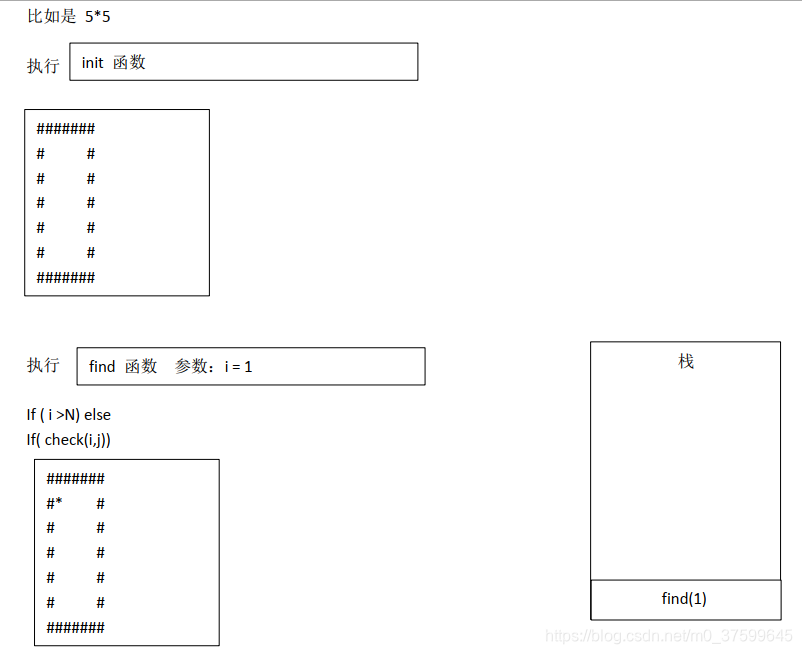


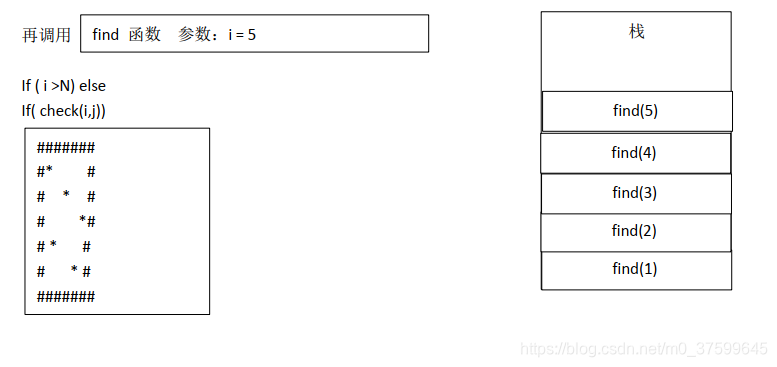
汇编:



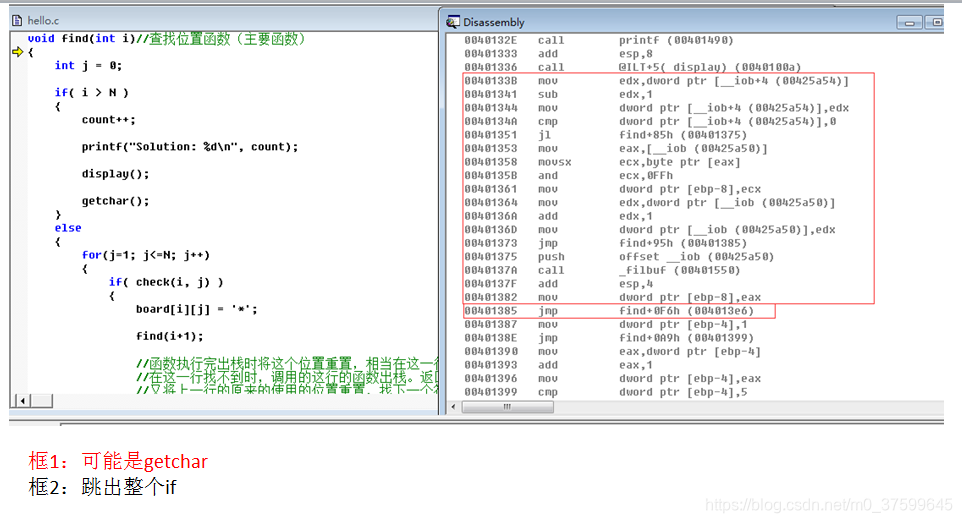
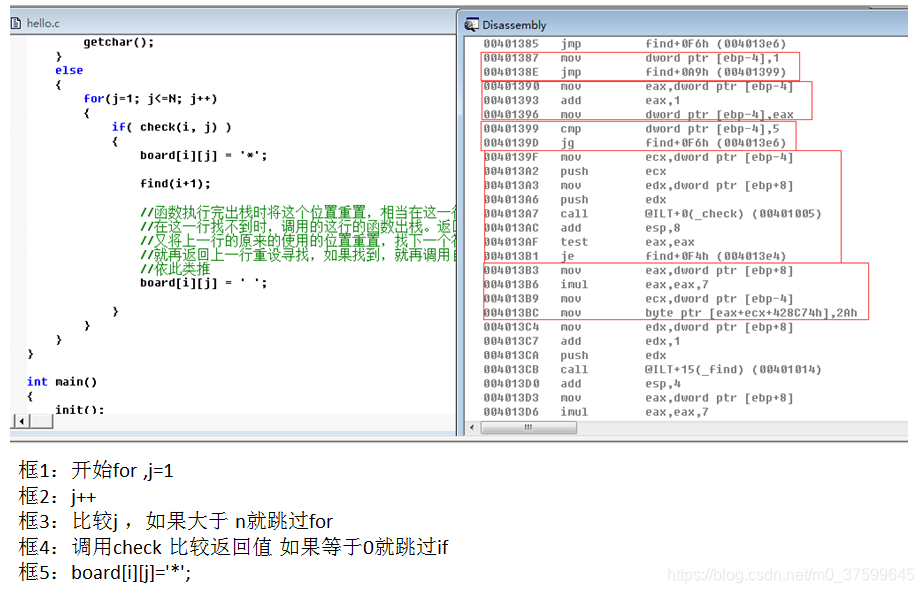






)

)




-(代码、分析、汇编))



方法与示例)
)

)
方法与示例)