树存储结构（代码、分析、汇编）

目录：

    • 代码：
    • 分析：
    • 汇编：

代码：

LinkList.h
LinkList.c
线性表

GTree.h

#ifndef _GTREE_H_
#define _GTREE_H_typedef void GTree;//定义树类型
typedef void GTreeData;//定义节点中存放数据的类型
typedef void (GTree_Printf)(GTreeData*);//定义一个参数是一个节点中存放数据的类型指针并且无返回值的函数类型GTree* GTree_Create();//声明创建树函数void GTree_Destroy(GTree* tree);//声明销毁树函数void GTree_Clear(GTree* tree);//声明清空树函数int GTree_Insert(GTree* tree, GTreeData* data, int pPos);//声明插入节点函数GTreeData* GTree_Delete(GTree* tree, int pos);//声明删除节点函数GTreeData* GTree_Get(GTree* tree, int pos);//声明获取节点函数GTreeData* GTree_Root(GTree* tree);//声明获取根节点函数int GTree_Height(GTree* tree);//声明获取高度函数int GTree_Count(GTree* tree);//声明获取节点数量函数int GTree_Degree(GTree* tree);//声明获取度数函数void GTree_Display(GTree* tree, GTree_Printf* pFunc, int gap, char div);//声明给每个节点数据进行操作函数#endif

GTree.c

#include <stdio.h>
#include <malloc.h>
#include "GTree.h"
#include "LinkList.h"typedef struct _tag_GTreeNode GTreeNode;//定义实际使用的树节点类型
struct _tag_GTreeNode
{GTreeData* data;//节点内存放的数据指针GTreeNode* parent;//节点的父节点LinkList* child;//节点的子节点（一个链表类型）
};typedef struct _tag_TLNode TLNode;//定义树节点与链表关联的类型（用于插入到链表的）
struct _tag_TLNode
{LinkListNode header;GTreeNode* node;
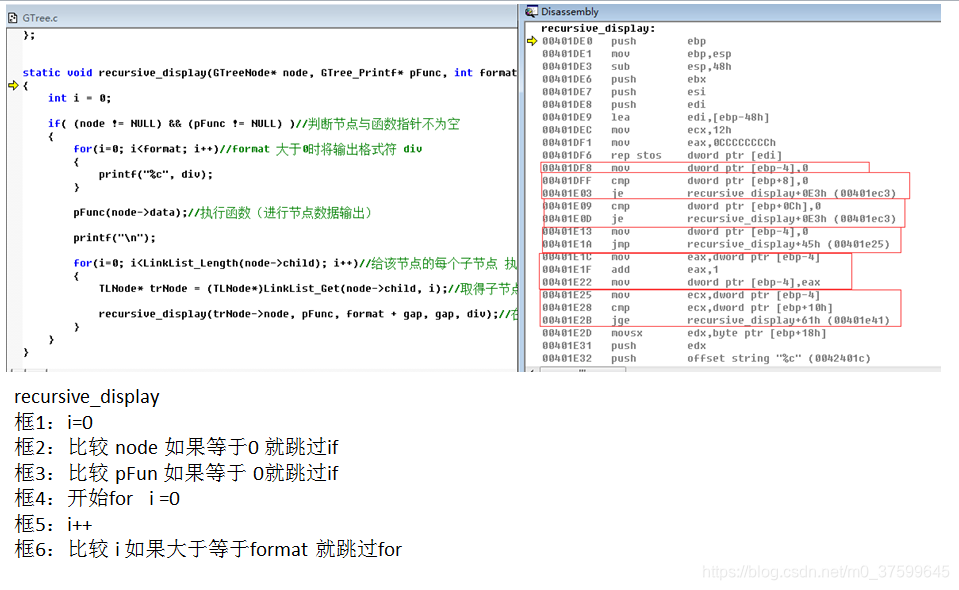
};static void recursive_display(GTreeNode* node, GTree_Printf* pFunc, int format, int gap, char div)
{int i = 0;if( (node != NULL) && (pFunc != NULL) )//判断节点与函数指针不为空{for(i=0; i<format; i++)//format 大于0时将输出格式符 div{printf("%c", div);}pFunc(node->data);//执行函数（进行节点数据输出）printf("\n");for(i=0; i<LinkList_Length(node->child); i++)//给该节点的每个子节点 执行相同操作{TLNode* trNode = (TLNode*)LinkList_Get(node->child, i);//取得子节点recursive_display(trNode->node, pFunc, format + gap, gap, div);//在每层子节点以2个格式占位符递增}}
}static void recursive_delete(LinkList* list, GTreeNode* node)//定义递归删除节点函数
{if( (list != NULL) && (node != NULL) )//判断链表与树节点不为空{GTreeNode* parent = node->parent;//取得删除节点的父节点int index = -1;int i = 0;for(i=0; i<LinkList_Length(list); i++)//在链表中找出要删除的节点{TLNode* trNode = (TLNode*)LinkList_Get(list, i);//取出链表中节点if( trNode->node == node )//如果该节点是要删除的树节点{LinkList_Delete(list, i);//将该节点从链表中删除free(trNode);//将该节点的空间释放（就是Insert函数中trNode申请的）index = i;//取得删除的下标break;}}if( index >= 0 )//如果在链表中删除了节点{  if( parent != NULL )//如果父节点不为空{for(i=0; i<LinkList_Length(parent->child); i++)//在父节点中的子链表中找到要删除的节点{TLNode* trNode = (TLNode*)LinkList_Get(parent->child, i);//在父节点中的子链表中取出要删除的节点if( trNode->node == node )//如果取出的节点是要删除的节点 {LinkList_Delete(parent->child, i);//将该节点从父节点的子链表中删除free(trNode);//该空间释放（就是Insert函数中cldNode申请的）break;}}               }while( LinkList_Length(node->child) > 0 )//如果删除节点还有子节点{TLNode* trNode = (TLNode*)LinkList_Get(node->child, 0);//取出删除节点中的子节点recursive_delete(list, trNode->node);//将要每个子节点执行同样操作}LinkList_Destroy(node->child);//这必须放在while后面，free(node);//释放树节点空间（就是Insert函数中cNode申请的）这必须放在while后面}}
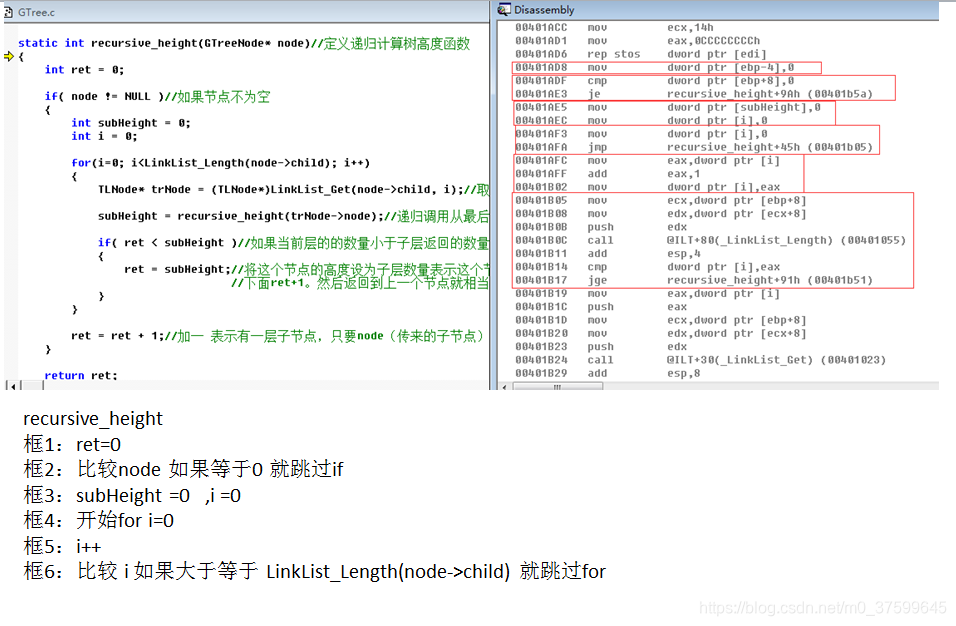
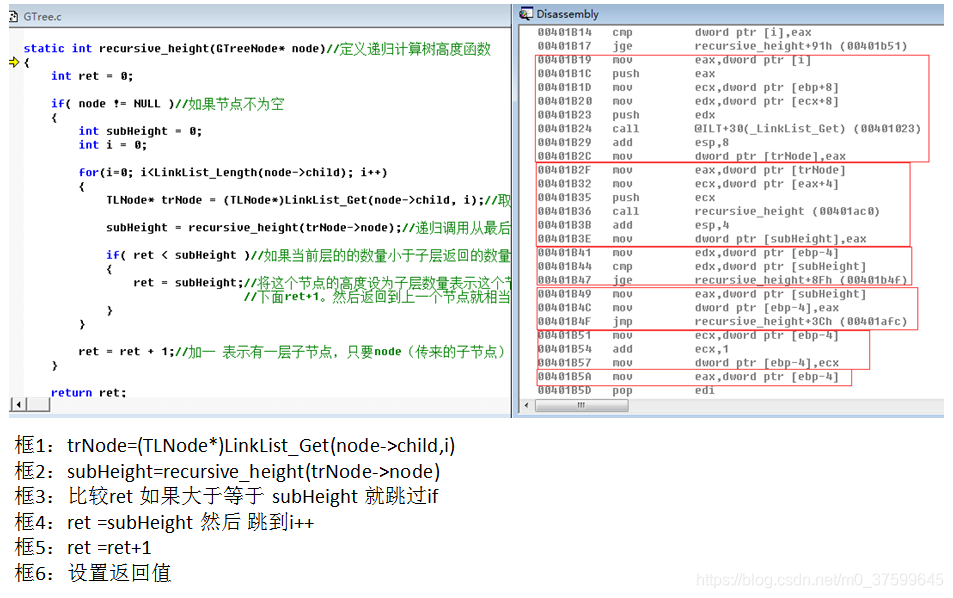
}static int recursive_height(GTreeNode* node)//定义递归计算树高度函数
{int ret = 0;if( node != NULL )//如果节点不为空{int subHeight = 0;int i = 0;for(i=0; i<LinkList_Length(node->child); i++){TLNode* trNode = (TLNode*)LinkList_Get(node->child, i);//取出子节点subHeight = recursive_height(trNode->node);//递归调用从最后一个子节点开始计算if( ret < subHeight )//如果当前层的的数量小于子层返回的数量{ret = subHeight;//将这个节点的高度设为子层数量表示这个节点下有这么多层子节点//下面ret+1。然后返回到上一个节点就相当再加上自己本身的这层}}ret = ret + 1;//加一 表示有一层子节点，只要node（传来的子节点）不为空必须加一}return ret;
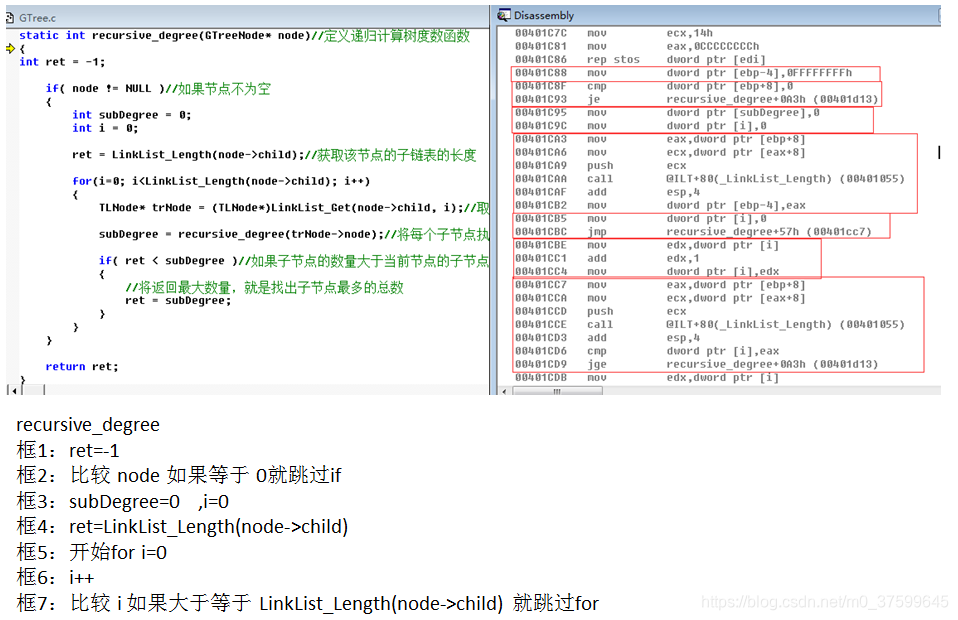
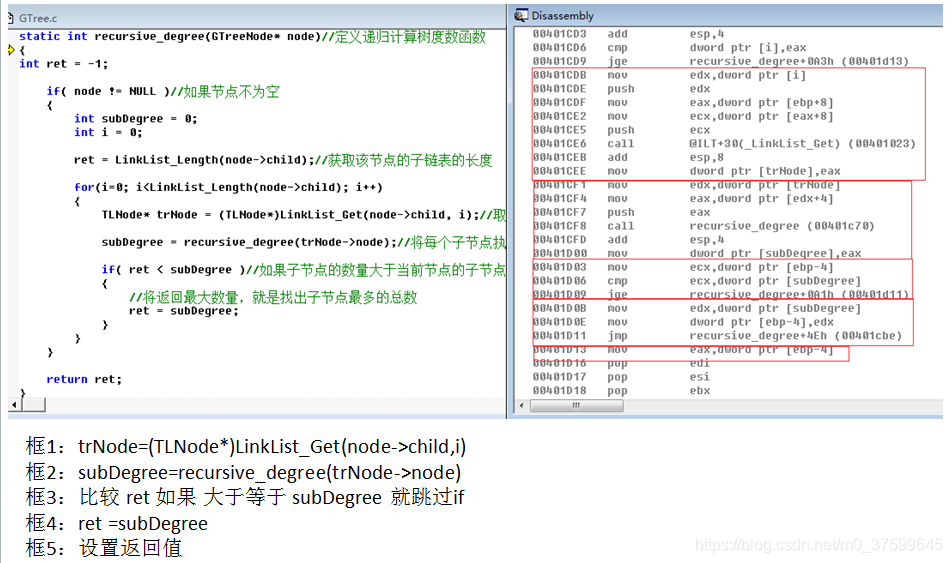
}static int recursive_degree(GTreeNode* node)//定义递归计算树度数函数
{
int ret = -1;if( node != NULL )//如果节点不为空{int subDegree = 0;int i = 0;ret = LinkList_Length(node->child);//获取该节点的子链表的长度for(i=0; i<LinkList_Length(node->child); i++){TLNode* trNode = (TLNode*)LinkList_Get(node->child, i);//取出子节点subDegree = recursive_degree(trNode->node);//将每个子节点执行同样操作if( ret < subDegree )//如果子节点的数量大于当前节点的子节点数量{//将返回最大数量，就是找出子节点最多的总数ret = subDegree;}}}return ret;
}GTree* GTree_Create()//定义创建树函数
{return LinkList_Create();//调用创建链表
}void GTree_Destroy(GTree* tree)//定义销毁树函数
{GTree_Clear(tree);LinkList_Destroy(tree);
}void GTree_Clear(GTree* tree)//定义清空树函数
{GTree_Delete(tree, 0);//删除根节点所有的子节点也会删除
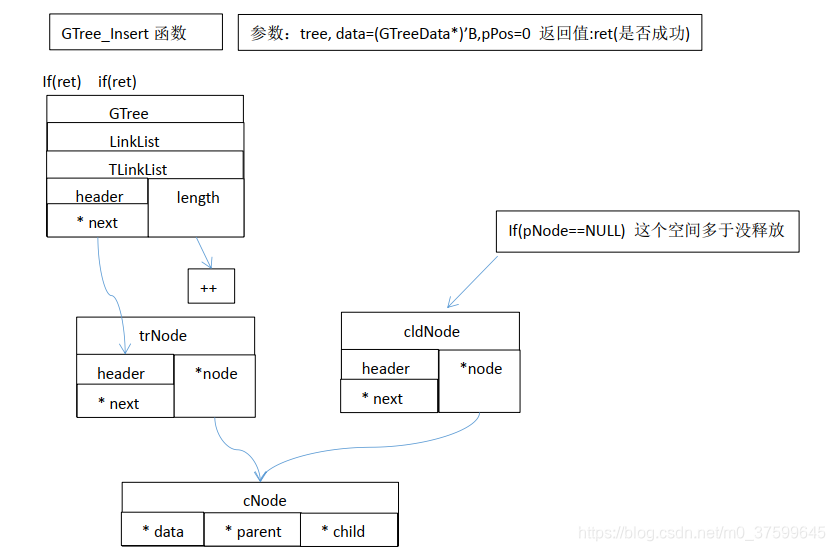
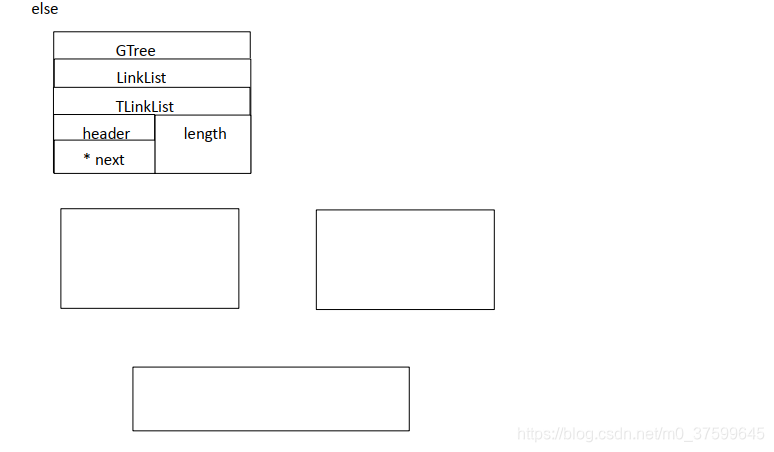
}int GTree_Insert(GTree* tree, GTreeData* data, int pPos)//定义插入节点函数
{LinkList* list = (LinkList*)tree;//将树指针转成链表指针int ret = (list != NULL) && (data != NULL) && (pPos < LinkList_Length(list));//判断表不为空插入的数据不为空与pPos正常if( ret )//条件成功{TLNode* trNode = (TLNode*)malloc(sizeof(TLNode));//新建树节点与链表关联类型// 注意：如果是下面pNode==NULL 。比如插入第一个节点时，后面这个cldNode申请的空间释放不了TLNode* cldNode = (TLNode*)malloc(sizeof(TLNode));//新建树节点与链表关联类型TLNode* pNode = (TLNode*)LinkList_Get(list, pPos);//获取出pPos位置的节点GTreeNode* cNode = (GTreeNode*)malloc(sizeof(GTreeNode));//新建一个树类型节点ret = (trNode != NULL) && (cldNode != NULL) && (cNode != NULL);//判断三个申请的空间成功if( ret )//条件成功{cNode->data = data;//给新建树节点中存放的数据赋值cNode->parent = NULL;//给新建树节点的父节点赋空cNode->child = LinkList_Create();//给新建节点的子节点赋值（新创建一个链表）trNode->node = cNode;//cldNode->node = cNode;LinkList_Insert(list, (LinkListNode*)trNode, LinkList_Length(list));//将新建节点插入链表最后一个位置if( pNode != NULL )//如果该位置本来有节点{cNode->parent = pNode->node;//将该位置本来有的节点赋给新建树节点的的父节点//使用树节点与链表关联类型将新建节点插入到该位置本来节点的子链表最后一个位置LinkList_Insert(pNode->node->child, (LinkListNode*)cldNode, LinkList_Length(pNode->node->child));}}else//如果条件不成功将申请的空间释放{free(trNode);free(cldNode);free(cNode);}}return ret;
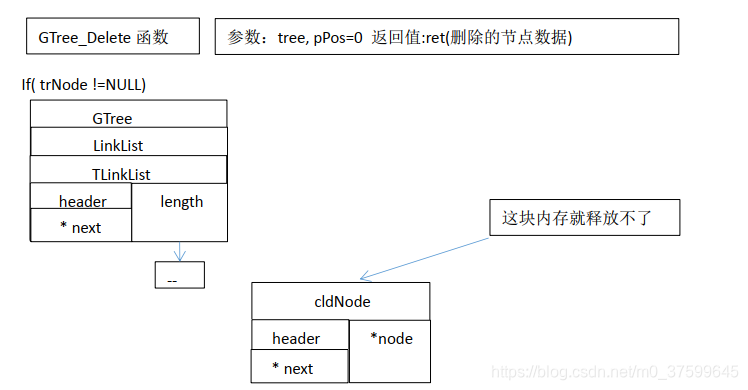
}GTreeData* GTree_Delete(GTree* tree, int pos)//定义删除节点函数
{TLNode* trNode = (TLNode*)LinkList_Get(tree, pos);//从链表中获取出删除位置节点GTreeData* ret = NULL;//定义指向删除节点中存放的数据的指针if( trNode != NULL )//如果有该位置节点{ret = trNode->node->data;//取得删除节点存放的数据//执行递归删除在总链表与其父节点子链表中移除该节点，再将该节点的子节点执行同样操作recursive_delete(tree, trNode->node);}return ret;//返回删除节点中存放的数据指针
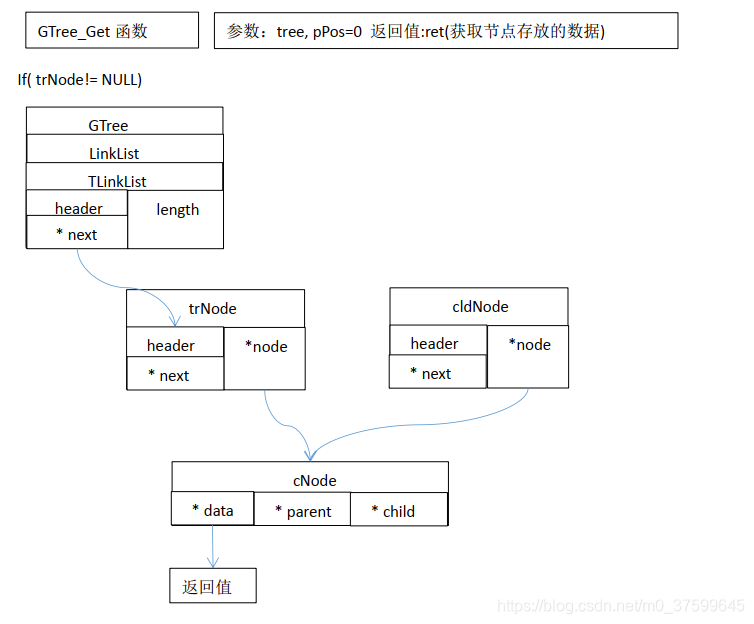
}GTreeData* GTree_Get(GTree* tree, int pos)//定义获取节点数据函数
{TLNode* trNode = (TLNode*)LinkList_Get(tree, pos);//从链表中获取出节点GTreeData* ret = NULL;if( trNode != NULL ){ret = trNode->node->data;//取得节点数据指针}return ret;//返回点中存放的数据指针
}GTreeData* GTree_Root(GTree* tree)//定义获取根节点数据函数
{return GTree_Get(tree, 0);//调用获取节点数据函数
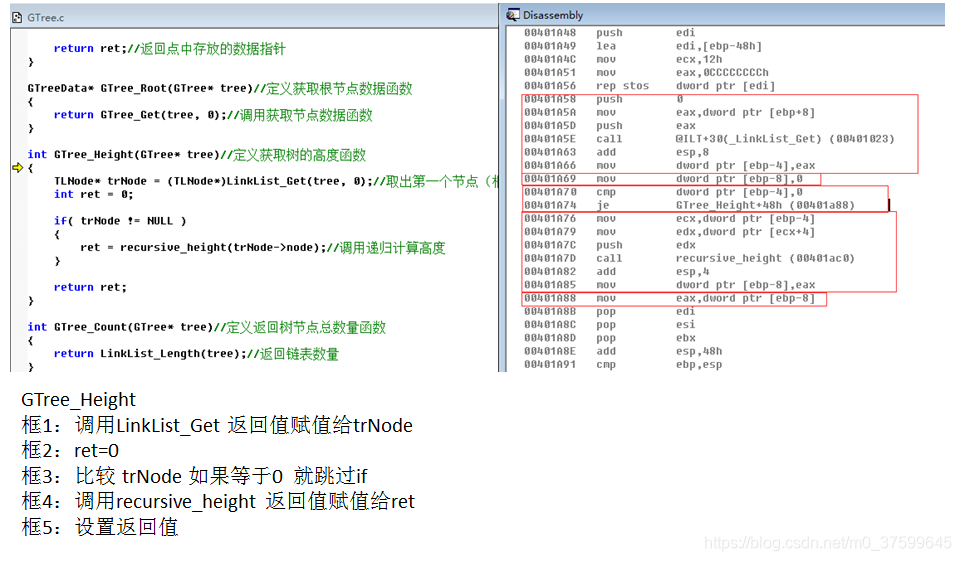
}int GTree_Height(GTree* tree)//定义获取树的高度函数
{TLNode* trNode = (TLNode*)LinkList_Get(tree, 0);//取出第一个节点（根节点）int ret = 0;if( trNode != NULL ){ret = recursive_height(trNode->node);//调用递归计算高度}return ret;
}int GTree_Count(GTree* tree)//定义返回树节点总数量函数
{return LinkList_Length(tree);//返回链表数量
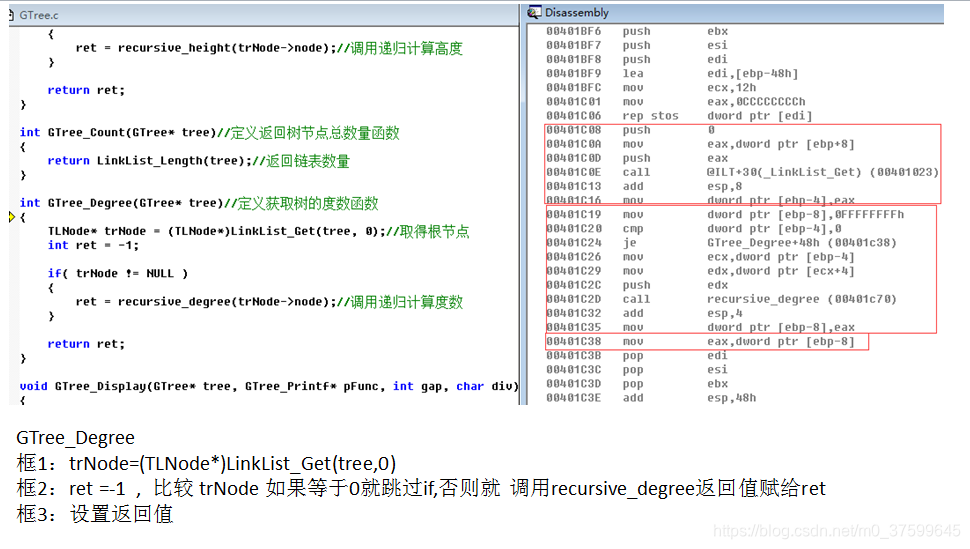
}int GTree_Degree(GTree* tree)//定义获取树的度数函数
{TLNode* trNode = (TLNode*)LinkList_Get(tree, 0);//取得根节点int ret = -1;if( trNode != NULL ){ret = recursive_degree(trNode->node);//调用递归计算度数}return ret;
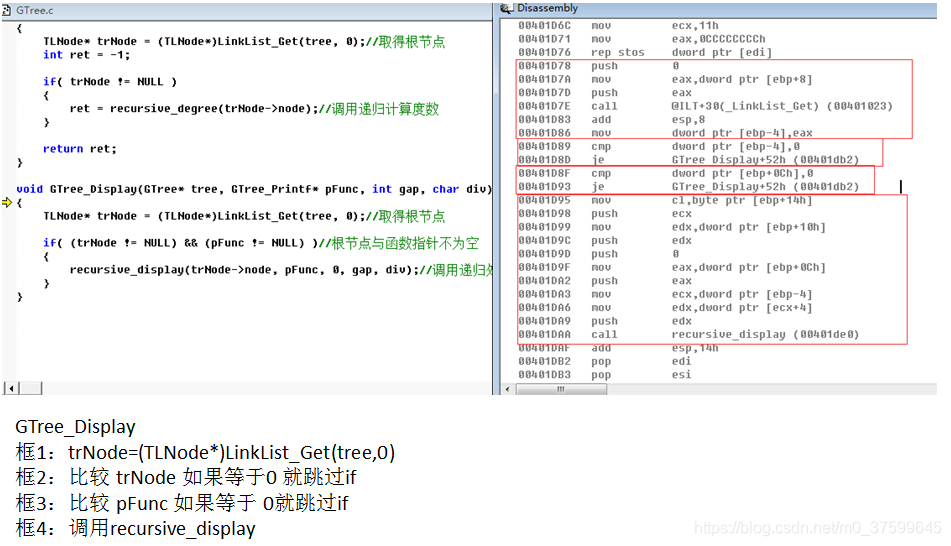
}void GTree_Display(GTree* tree, GTree_Printf* pFunc, int gap, char div)//定义给每个节点数据进行操作函数
{TLNode* trNode = (TLNode*)LinkList_Get(tree, 0);//取得根节点if( (trNode != NULL) && (pFunc != NULL) )//根节点与函数指针不为空{  recursive_display(trNode->node, pFunc, 0, gap, div);//调用递归处理}
}

main.c

#include <stdio.h>
#include "GTree.h"
void printf_data(GTreeData* data)
{printf("%c", (int)data);
}int main(int argc, char *argv[])
{GTree* tree = GTree_Create();int i = 0;GTree_Insert(tree, (GTreeData*)'A', -1);GTree_Insert(tree, (GTreeData*)'B', 0);GTree_Insert(tree, (GTreeData*)'C', 0);GTree_Insert(tree, (GTreeData*)'D', 0);GTree_Insert(tree, (GTreeData*)'E', 1);GTree_Insert(tree, (GTreeData*)'F', 1);GTree_Insert(tree, (GTreeData*)'H', 3);GTree_Insert(tree, (GTreeData*)'I', 3);GTree_Insert(tree, (GTreeData*)'J', 3);printf("Tree Height: %d\n", GTree_Height(tree));printf("Tree Degree: %d\n", GTree_Degree(tree));printf("Full Tree:\n");GTree_Display(tree, printf_data, 2, ' ');printf("Get Tree Data:\n");for(i=0; i<GTree_Count(tree); i++){printf_data(GTree_Get(tree, i));printf("\n");}printf("Get Root Data:\n");printf_data(GTree_Root(tree));printf("\n");GTree_Delete(tree, 3);printf("After Deleting D:\n");GTree_Display(tree, printf_data, 2, '-');GTree_Clear(tree);printf("After Clearing Tree:\n");GTree_Display(tree, printf_data, 2, '.');GTree_Destroy(tree);getchar();return 0;
}

分析：

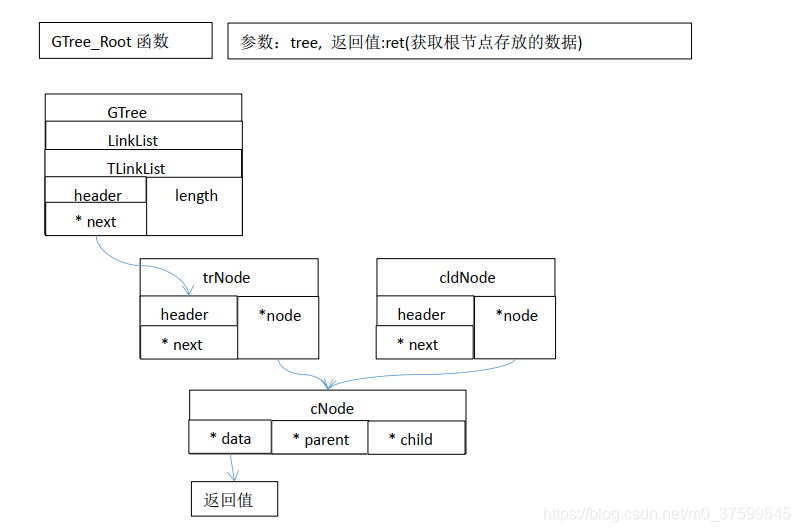
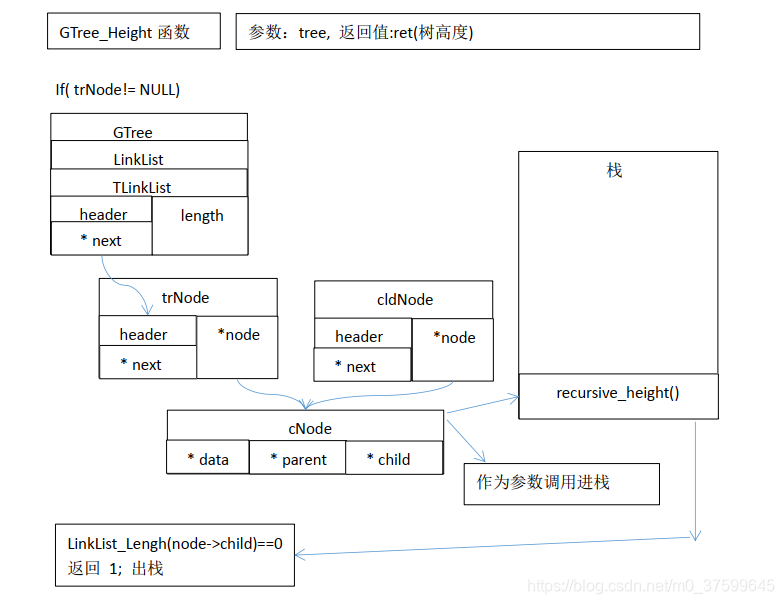
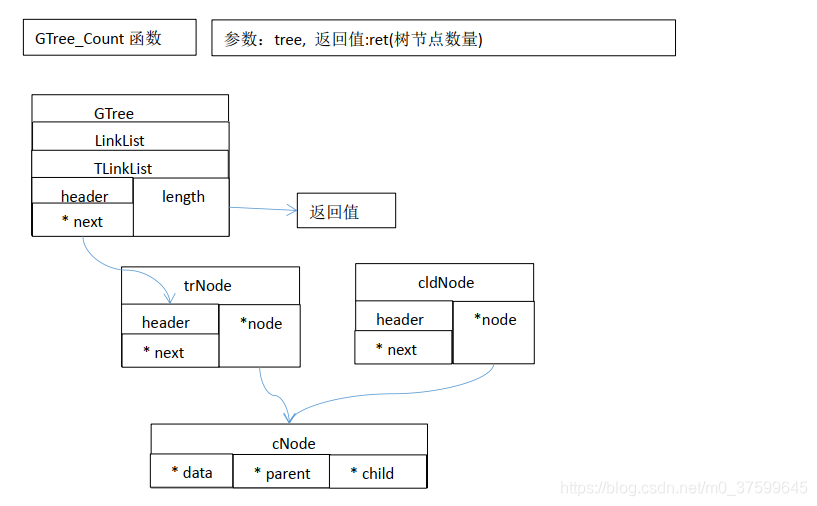
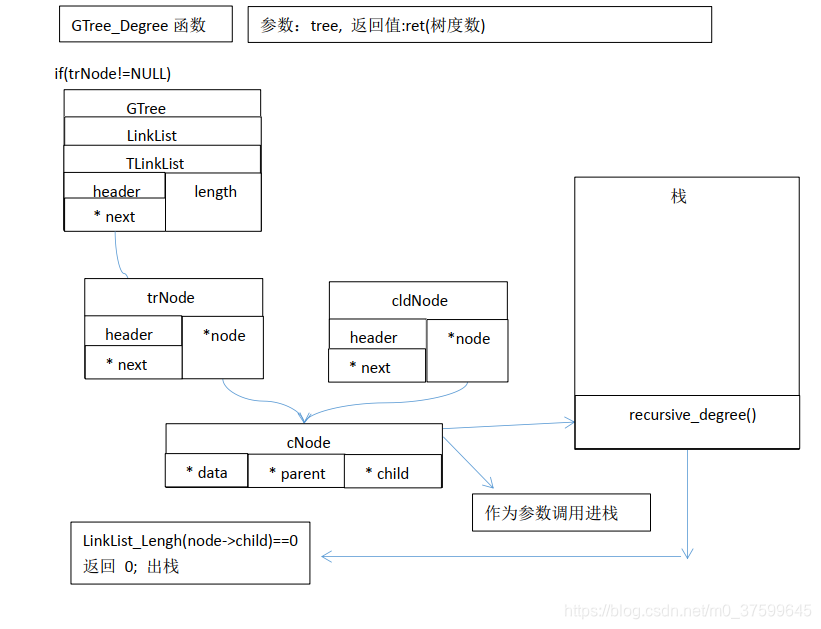
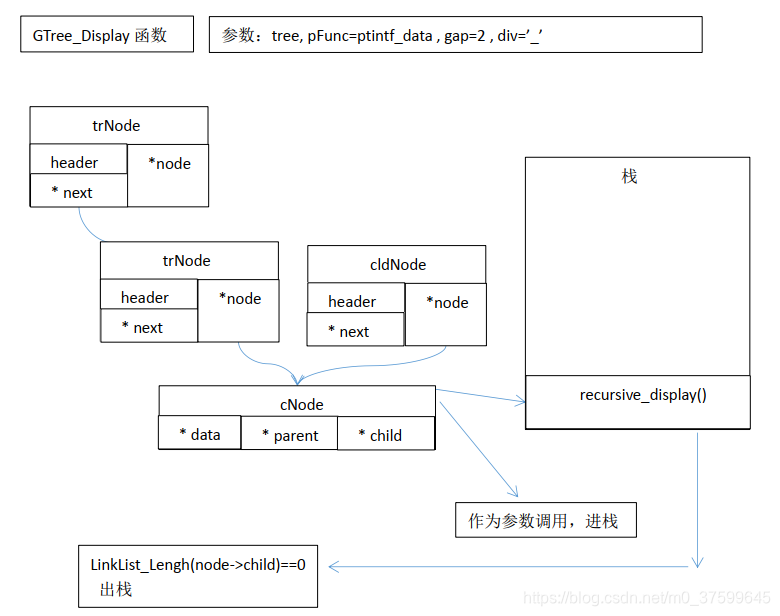
在这里插入图片描述
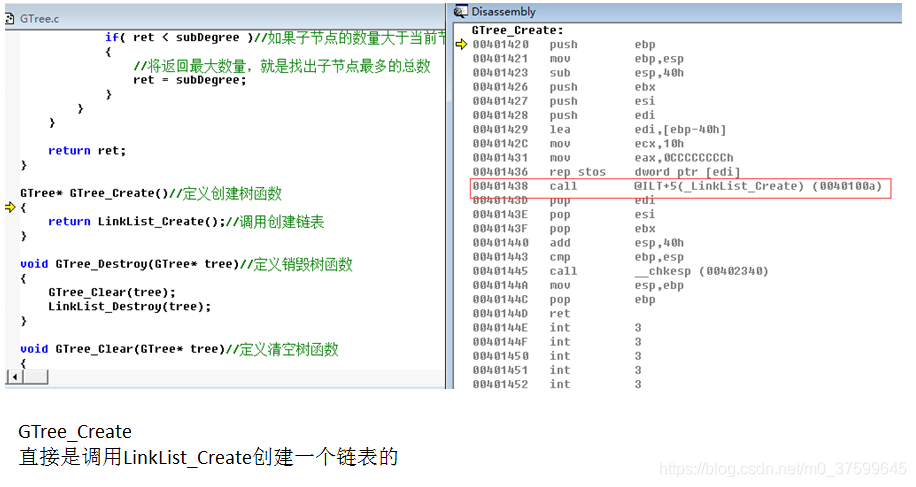
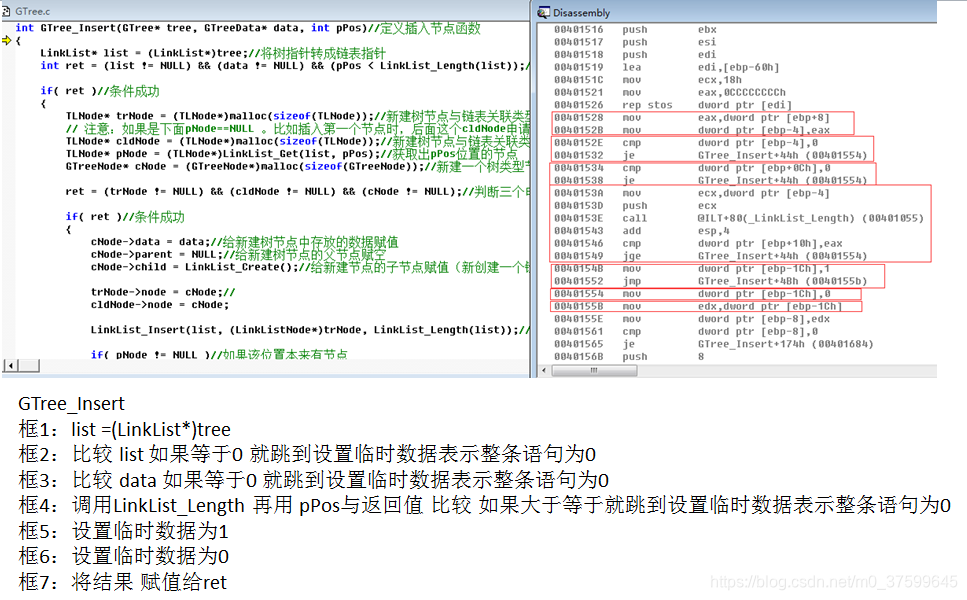
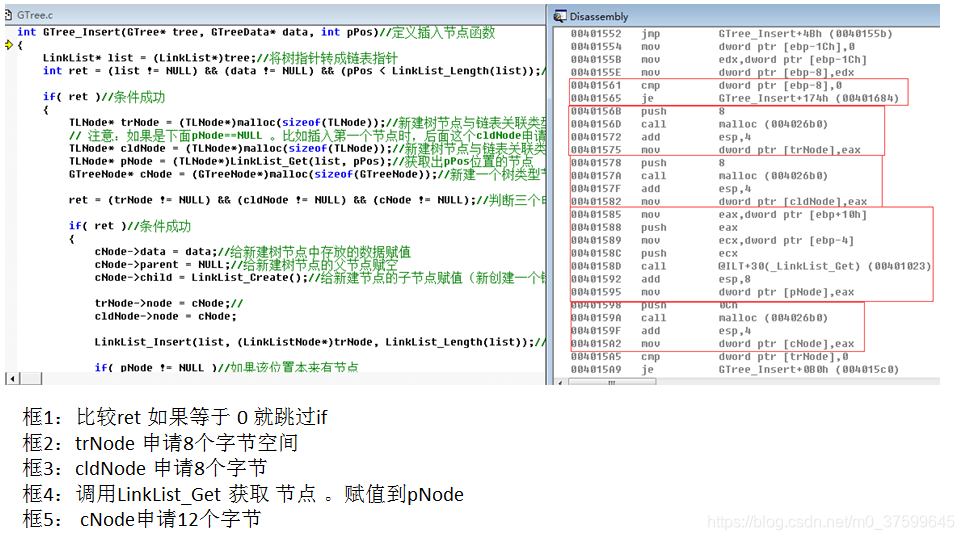
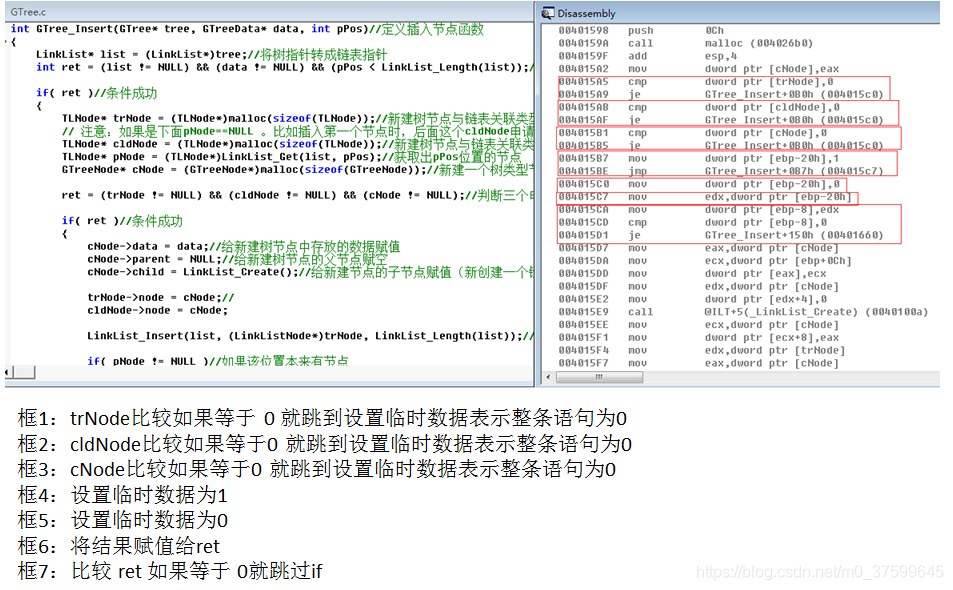
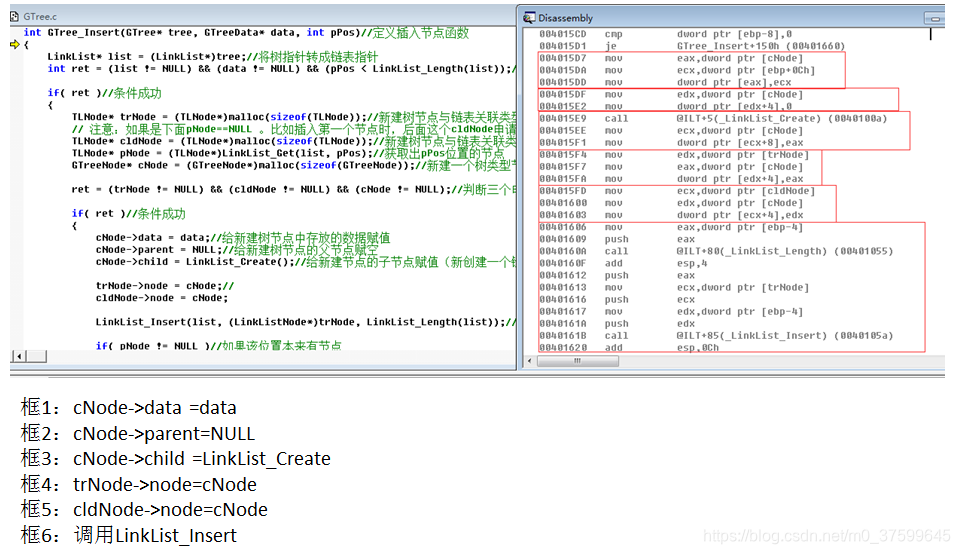
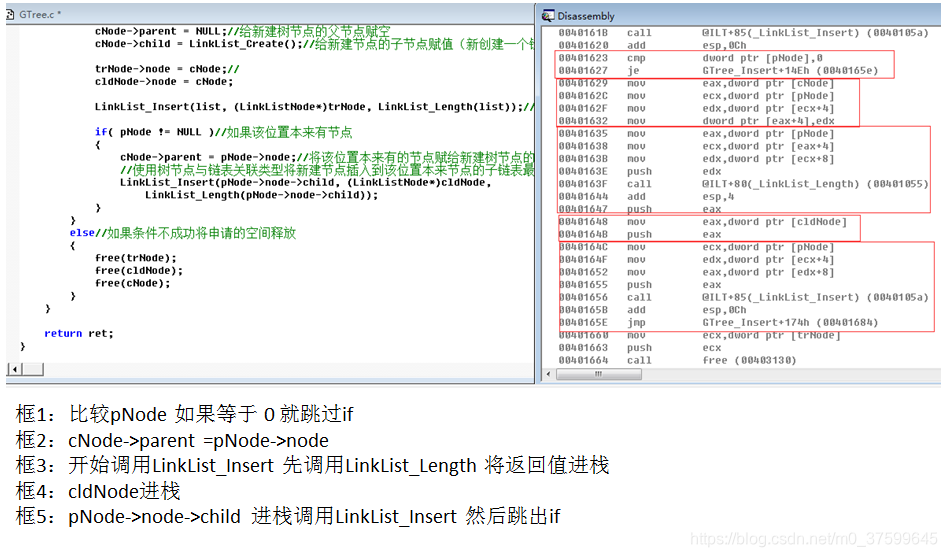
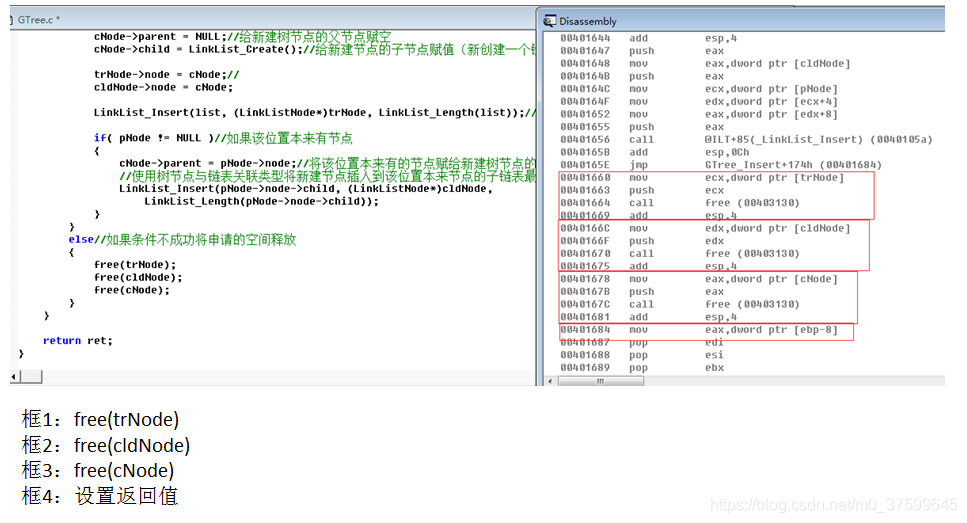
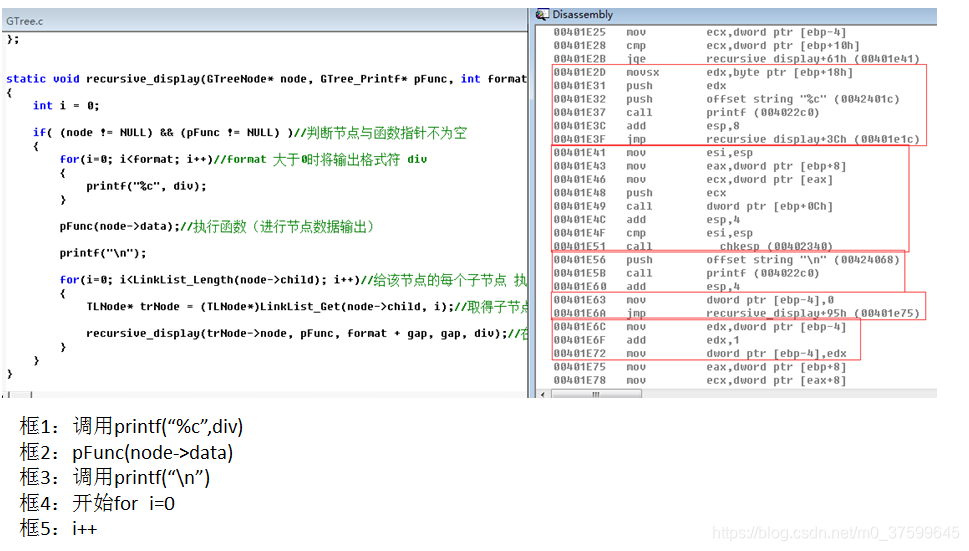
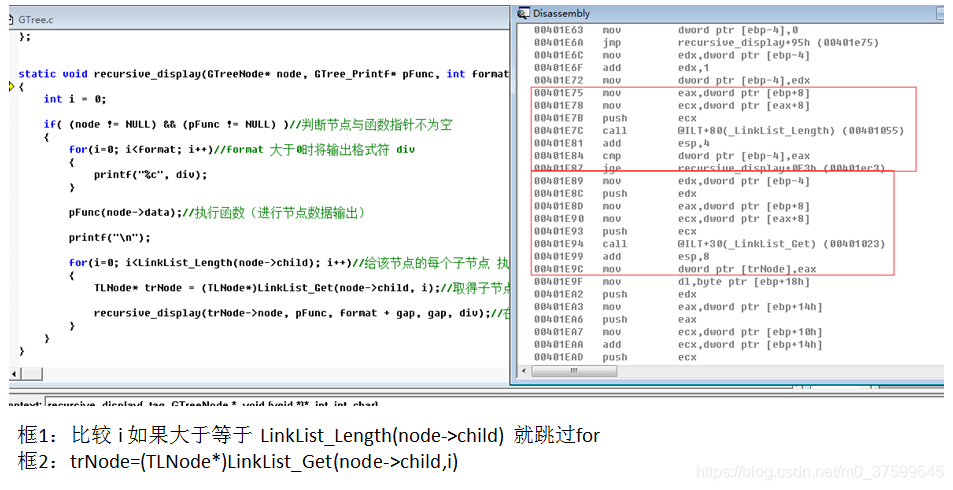
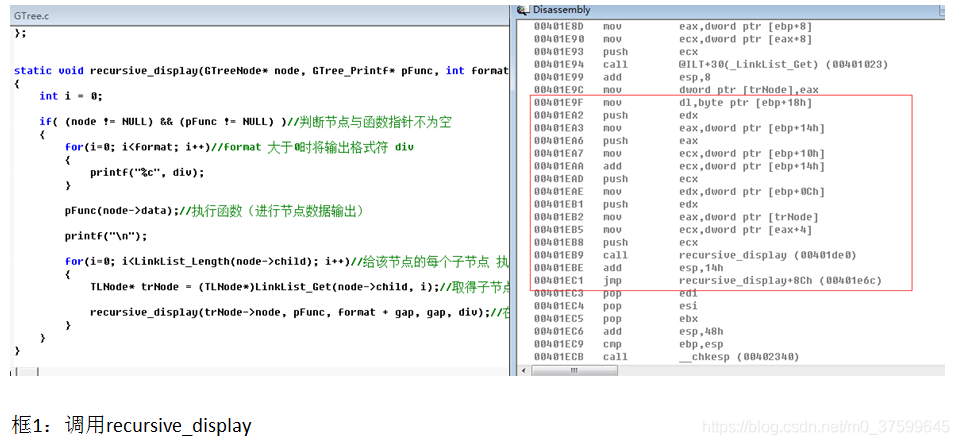
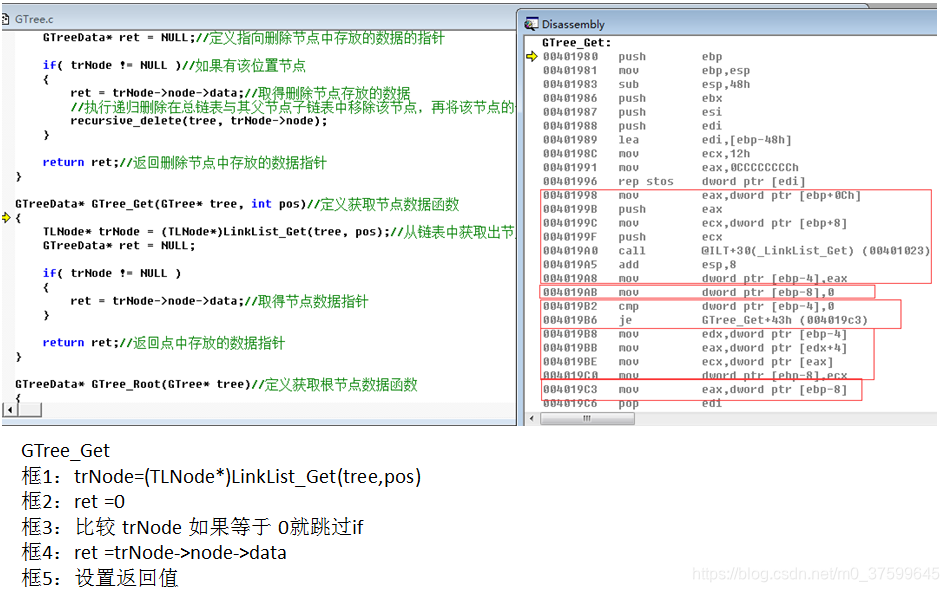
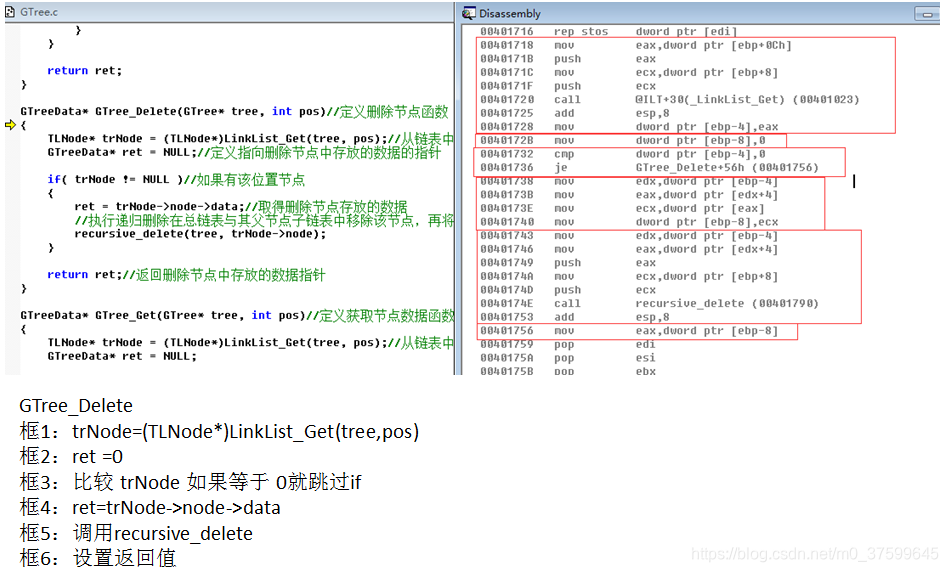
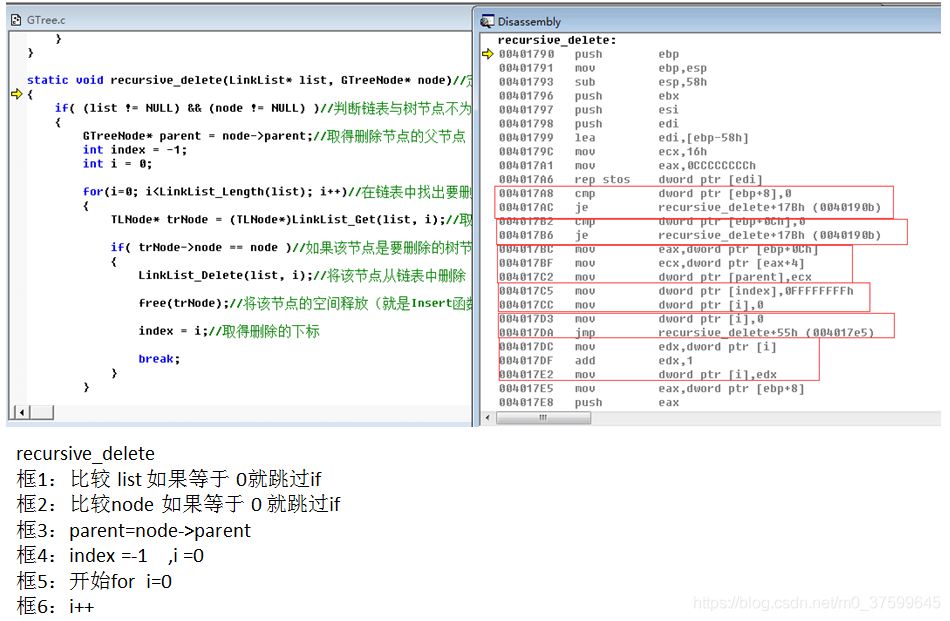
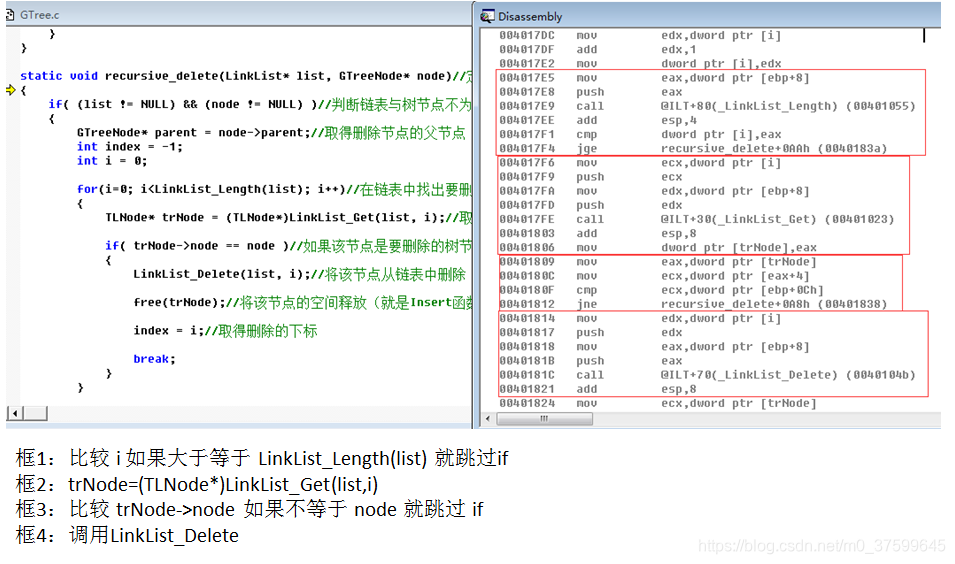
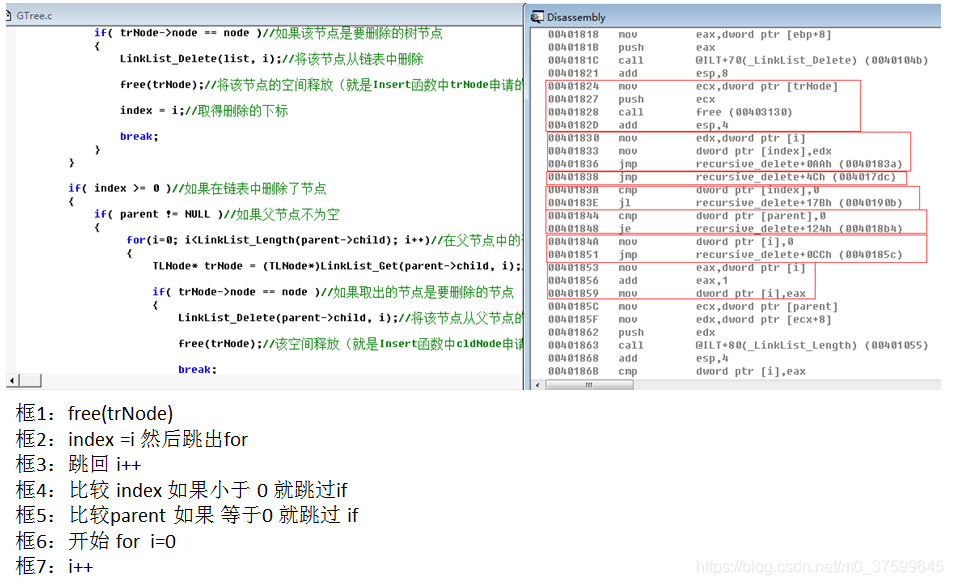
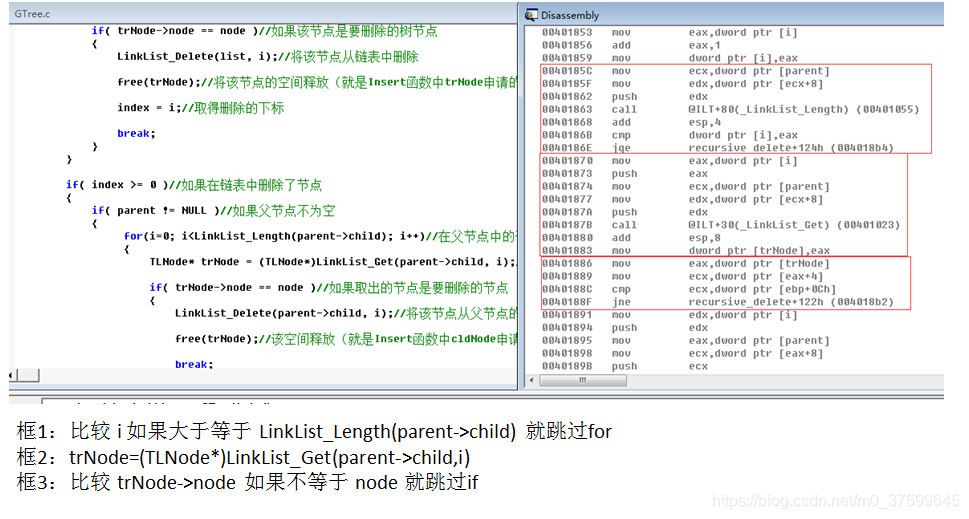
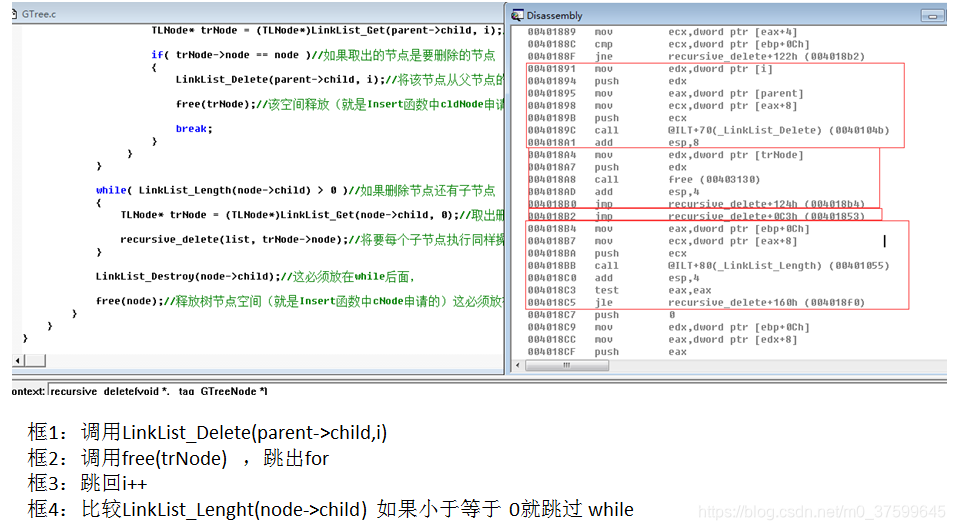
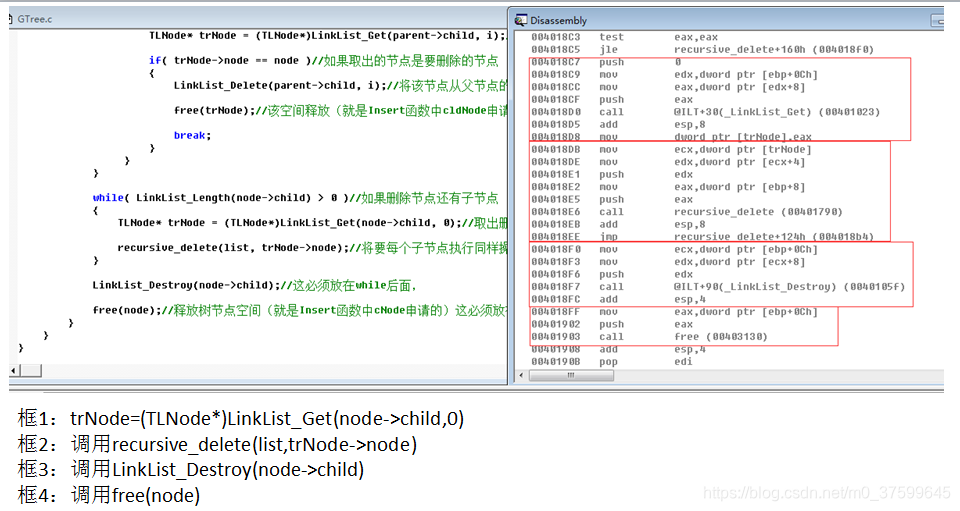
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

汇编：

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/379185.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

二元矩阵峰值搜索_好斗的牛（二元搜索）

二元矩阵峰值搜索_好斗的牛（二元搜索）

二元矩阵峰值搜索A farmer has built a long barn with N stalls. The stalls are placed in a straight manner at positions from x1, x2, ...xN. But his cows (C) are aggressive and don’t want to be near other cows. To prevent cows from hurting each other, he wan…
阅读更多...
Python---冒泡排序、选择排序

Python---冒泡排序、选择排序

冒泡排序 依次输入n个数&#xff0c;进行冒泡排序 冒泡排序法&#xff0c;即两个相邻的进行比较&#xff0c;比较之后换位置 def bubbleSort(arr):n len(arr)for i in range(n):for j in range(0, n-i-1):if arr[j] > arr[j1] :arr[j], arr[j1] arr[j1], arr[j]arr[] n…
阅读更多...
react js 添加样式_如何在React JS Application中添加图像？

react js 添加样式_如何在React JS Application中添加图像？

react js 添加样式Hello! In this article, we will learn how to add images in React JS? I remember when I just started coding in React JS, I thought adding images would be done exactly as it is in HTML. I later realized that it was different. 你好&#xff0…
阅读更多...
二叉树（多路平衡搜索树）-（代码、分析、汇编）

二叉树（多路平衡搜索树）-（代码、分析、汇编）

目录&#xff1a;代码&#xff1a;分析&#xff1a;汇编&#xff1a;代码&#xff1a; BTree.h #ifndef _BTREE_H_ #define _BTREE_H_#define BT_LEFT 0 //定义左子节点标识 #define BT_RIGHT 1 //定义右子节点标识typedef void BTree;//定义树类型 typedef unsigned long lo…
阅读更多...
Python---二分法查找

Python---二分法查找

输入n个数&#xff0c;通过二分法查找该数的下标 def binarySearch(arr,value):m 0#开始n len(arr#最后)while m<n:mid(mn)//2#计算中间位置if valuearr[mid]:#查找成功&#xff0c;返回元素对应的位置return midelif value>arr[mid]:#在后面一半元素中继续查找mmid1e…
阅读更多...
SQL捕获异常

SQL捕获异常

原文地址 http://technet.microsoft.com/zh-cn/office/ms179296%28vsql.100%29在 Transact-SQL 中使用 TRY...CATCHTransact-SQL 代码中的错误可使用 TRY…CATCH 构造处理&#xff0c;此功能类似于 Microsoft Visual C 和 Microsoft Visual C# 语言的异常处理功能。TRY…CATCH …
阅读更多...
二叉树遍历（代码，分析，汇编）

二叉树遍历（代码，分析，汇编）

目录&#xff1a;代码&#xff1a;分析&#xff1a;汇编&#xff1a;代码&#xff1a; BTree.h BTree.c 二叉树&#xff08;多路平衡搜索树&#xff09; LinkQueue.h #ifndef _LINKQUEUE_H_ #define _LINKQUEUE_H_typedef void LinkQueue;//定义队列类型LinkQueue* LinkQueu…
阅读更多...
Python---查找序列的最长递增子序列

Python---查找序列的最长递增子序列

查找序列的最长递增子序列 什么是序列的最长递增子序列&#xff1f; 答&#xff1a;在一个数值序列中&#xff0c;找到一个子序列&#xff0c;使得这个子序列元素的数值依次递增&#xff0c;并且这个子序列的长度尽可能地大。这就是所谓的最长递增子序列 from itertools impo…
阅读更多...
ffmpeg-从mp4、flv、ts文件中提取264视频流数据

ffmpeg-从mp4、flv、ts文件中提取264视频流数据

ffmpeg-从mp4、flv、ts文件中提取264视频流数据 main.c #include <stdio.h> #include <libavutil/log.h> #include <libavformat/avio.h> #include <libavformat/avformat.h>void proc(int need_to_annexb, char* in_file, char* out_file) {AVForma…
阅读更多...
线索化二叉树（代码 、分析 、汇编）

线索化二叉树（代码 、分析 、汇编）

目录&#xff1a;代码&#xff1a;分析&#xff1a;汇编&#xff1a;代码&#xff1a; BTree.h BTree.c 二叉树&#xff08;多路平衡搜索树&#xff09; SeqList.h SeqList.c 顺序表 main.c #include <stdio.h> #include <stdlib.h> #include "BTree.h&qu…
阅读更多...
Python---寻找给定序列中相差最小的两个数字

Python---寻找给定序列中相差最小的两个数字

编写函数&#xff0c;寻找给定序列中相差最小的两个数字 def getTwoClosestElements(arr):#先进行排序&#xff0c;使得相邻元素最接近#相差最小的元素必然相邻seq sorted(arr)#先进行排序dif float(inf)#无穷大#遍历所有元素&#xff0c;两两比较&#xff0c;比较相邻元素的…
阅读更多...
Python---利用蒙特.卡罗方法计算圆周率近似值

Python---利用蒙特.卡罗方法计算圆周率近似值

利用蒙特.卡罗方法计算圆周率近似值 什么是蒙特.卡罗方法&#xff1f; 答&#xff1a;蒙特卡罗方法是一种计算方法。原理是通过大量随机样本&#xff0c;去了解一个系统&#xff0c;进而得到所要计算的值。 正方形内部有一个相切的圆&#xff0c;它们的面积之比是π/4。 这里假…
阅读更多...
FLV封装格式的分析

FLV封装格式的分析

FLV封装格式的分析&#xff0c;各种详细的参数比较多没有详细解释&#xff0c;这是总体的格式分布。详细的参数说明可以参照文档。 以flv格式内封装的音频流是aac、视频流是h264分析&#xff1a; flv文件tag部分截图&#xff1a;可以看到音频TAG、视频TAG是交错存储的
阅读更多...
《计算机基础复习》===数据库技术基础

《计算机基础复习》===数据库技术基础

数据库系统三级结构&#xff1a; 数据库系统一般划分为三个抽象级&#xff1a;用户级、概念级、物理级。 1&#xff09;用户级数据库&#xff1a;对应于外模式。它是用户看到和使用的数据库&#xff0c;又称用户视图&#xff1b;用户级数据库主要由外部记录组成&#xff0c;不同…
阅读更多...
bs架构 erp 进销存_从依赖经验到用柔性ERP，企业少走了多少弯路？

bs架构 erp 进销存_从依赖经验到用柔性ERP，企业少走了多少弯路？

企业在面对紧急订单时&#xff0c;传统企业将面临两难问题&#xff1a;如不接受紧急订单,可能会导致潜在的顾客丢失,损失市场占有率;接受紧急订单,可能会给企业带来很多管理上的问题,如材料采购、库存管理等。而企业通过信息化手段提升生产计划与控制的柔性&#xff0c;则可从容…
阅读更多...
云端: 小软件大平台,绿色又安全 V0.9 Beta3（090722）

云端: 小软件大平台,绿色又安全 V0.9 Beta3（090722）

云端 是一个小软件&#xff0c;但又是一个大平台。安装云端之后&#xff0c;再使用其他软件不再需要安装——一点、下载、直接使用&#xff1b;并且&#xff0c;通过虚拟化的运行环境&#xff0c;能够保持系统长久的干净、绿色&#xff0c;并保持软件与系统的安全隔离——此方面…
阅读更多...
MGraph图（代码、分析、汇编）

MGraph图（代码、分析、汇编）

目录:代码&#xff1a;分析&#xff1a;汇编&#xff1a;MGrapth图表示有邻接矩阵的方式构成的图结构。邻接矩阵用两个数组保存数据&#xff0c;一个一维数组存储图中的顶点信息&#xff0c;一个二维数组存储图中边或弧的信息。无向图中的二维数组是个对称矩阵 1.0表示无边&…
阅读更多...
java: 程序包lombok不存在_Java开发神器：Lombok 学习指南

java: 程序包lombok不存在_Java开发神器：Lombok 学习指南

点击上方“Java知音”&#xff0c;选择“置顶公众号”技术文章第一时间送达&#xff01;作者&#xff1a;semlinkerwww.segmentfault.com/a/1190000020864572一、Lombok 简介Lombok 是一款 Java 开发插件&#xff0c;使得 Java 开发者可以通过其定义的一些注解来消除业务工程中…
阅读更多...
AAC ADTS格式分析

AAC ADTS格式分析

AAC ADTS格式分析&#xff1a; 没有详细的参数说明&#xff0c;只有格式分析。可以查询文档查看详细参数说明。 ADTS的全称是Audio Data Transport Stream。是AAC音频的传输流格 式。AAC音频格式在MPEG-2&#xff08;ISO-13318-7 2003&#xff09;中有定义。AAC后来 又被采用到…
阅读更多...
新知道的几个东西

新知道的几个东西

nginx&#xff08;发音同engine x&#xff09;是一款由俄罗斯程序设计师Igor Sysoev所开发轻量级的网页服务器、反向代理服务器以及电子邮件&#xff08;IMAP/POP3&#xff09;代理服务器。起初是供俄国大型的入口网站及搜寻引擎Rambler&#xff08;俄文&#xff1a;Рамбл…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023