曲线斜纹组织图:
因为其形状酷似抛物线,抛物线又是曲线中的一种,故称为曲线斜纹组织。
特点:1,每一根经纱上的组织点运动规律不变
2,飞数是变化的,故也称为变飞数组织
飞数满足的两个条件:
Ⅰ所有的飞数之和必须等于基层组织循环数的整倍数或者零。这样做才能保证组织的连续性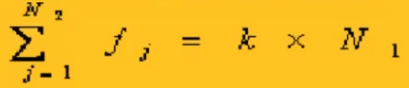
Ⅱ最大飞数必须小于基层组织中最长的浮线长度(连续的组织点个数)
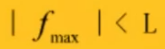
例如:3上2下2上1下,其中最长的浮线长度为3,飞数必须小于3。
一、确定经纬纱循环数
经纱循环数还是一般式的累计和
纬纱循环数为飞数的个数+1,因为5个飞数可以确定6列,故列数为飞数个数+1
二、对第一列赋值
老规矩,从下往上,从左往右
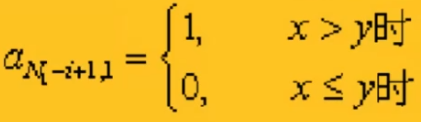
核心代码如下:
/*
对第1列进行赋值
*/i=1;//先对第一列赋值,从第一列的第一行开始for(j=0;j<m;j++){while(c[j]>0){a[N1-i+1][1]=1;//因为是分子,所有值都赋值为1c[j]--;i++;}while(d[j]>0){a[N1-i+1][1]=0;//因为是分母,所有值都赋值为0d[j]--;i++;}}
效果图如下:
在这里插入图片描述
三、根据飞数进行依次按规则组织方式赋值
这里根据每一个飞数求出对应一列
飞数为负数时需要进行转换,公式如下: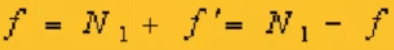
对第2列到第N2列进行赋值,赋值关系如下:

核心代码如下:
/*
将负飞数转化为正数
*/for(i=1;i<=number;i++){if(f[i]<0)f[i]=N1+f[i];}/*
对2到N2列 进行赋值
*/for(j=2;j<=N2;j++){for(i=1;i<=N1;i++){if((i+f[j-1])>N1) a[i][j] = a[i+f[j-1]-N1][j-1];else a[i][j]=a[i+f[j-1]][j-1];}}四、最终整合代码如下:
#include <iostream>
#include<stdio.h>
using namespace std;int main()
{int i,j,N1,N2,m,number;int c[10],d[10],f[20],a[100][100]={0};printf("please input m:");scanf("%d",&m);for(i=0;i<m;i++){printf("please input C[%d]:",i+1);scanf("%d",&c[i]);printf("please input D[%d]:",i+1);scanf("%d",&d[i]);}printf("please input the number of f:");scanf("%d",&number);for(i=1;i<=number;i++){printf("please input f[%d]:",i);scanf("%d",&f[i]);}N1=0;N2=number+1;for(i=0;i<=m-1;i++){N1=N1+c[i]+d[i];}/*
对第1列进行赋值
*/i=1;//先对第一列赋值,从第一列的第一行开始for(j=0;j<m;j++){while(c[j]>0){a[N1-i+1][1]=1;//因为是分子,所有值都赋值为1c[j]--;i++;}while(d[j]>0){a[N1-i+1][1]=0;//因为是分母,所有值都赋值为0d[j]--;i++;}}/*
将负飞数转化为正数
*/for(i=1;i<=number;i++){if(f[i]<0)f[i]=N1+f[i];}/*
对2到N2列 进行赋值
*/for(j=2;j<=N2;j++){for(i=1;i<=N1;i++){if((i+f[j-1])>N1) a[i][j] = a[i+f[j-1]-N1][j-1];else a[i][j]=a[i+f[j-1]][j-1];}}/*
输出二维数组a[i][j]
*/for(i=1;i<=N1;i++){for(j=1;j<=N2;j++){printf("%5d",a[i][j]);}printf("\n");}getchar();return 0;
}效果图如下: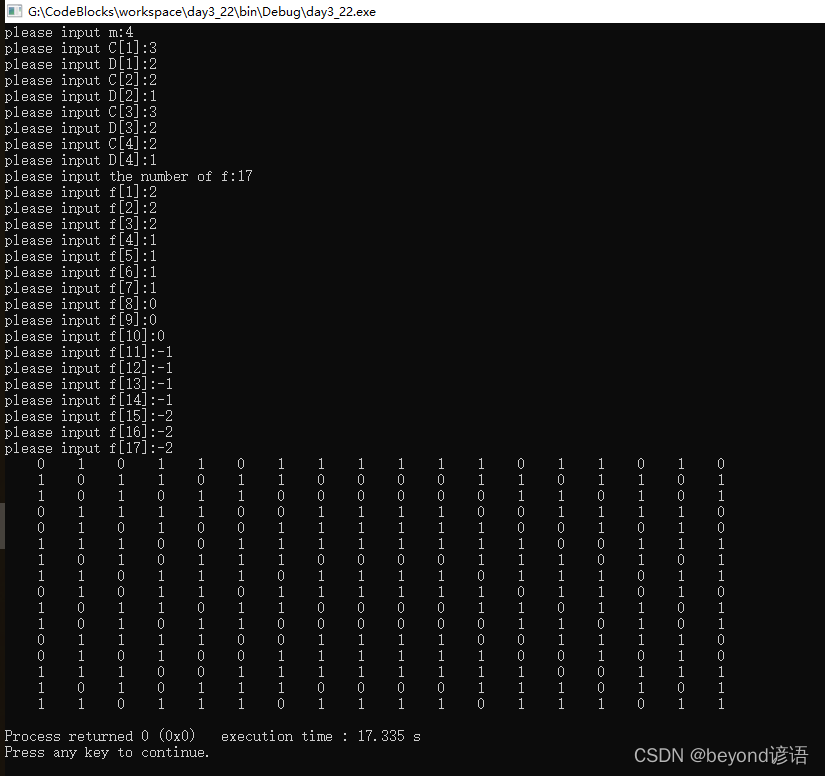
方法及示例)


)



方法与示例)

)
)


方法与示例)





方法与示例)