十三、图像梯度

一、两种算子

一阶导数—Sobel算子

水平梯度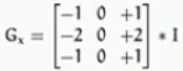：在这里插入图片描述

垂直梯度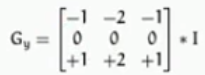：在这里插入图片描述

最终图像梯度：
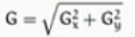
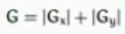
在这里插入图片描述

二阶导数—Laplacian算子

在二阶导数的时候，最大变化处的值为零，即边缘是零值。
常见的拉普拉斯算子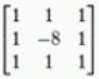：在这里插入图片描述、其所有元素之和为零。

二、Sobel算子

cv2.Sobel(image,cv2.CV_32F,1,0)image为代求的图像；CV_32F为图像的深度(32为float类型)，255肯定不够，故选择大点
cv2.convertScaleAbs(grad_x)将计算出来的正负数全部转换为正值，然后转换到8位的图像上去

import cv2
import numpy as np
from matplotlib import pyplot as pltdef sobel(image):grad_x = cv2.Sobel(image,cv2.CV_32F,1,0)grad_y = cv2.Sobel(image,cv2.CV_32F,0,1)gradx = cv2.convertScaleAbs(grad_x)grady = cv2.convertScaleAbs(grad_y)cv2.imshow("gradient-x",gradx)cv2.imshow("gradient-y",grady)gradxy = cv2.addWeighted(gradx,0.5,grady,0.5,0)cv2.imshow("gradient",gradxy)src = cv2.imread(r"G:\Juptyer_workspace\study\opencv\opencv3\a1.jpg")
cv2.imshow("image",src)
cv2.namedWindow("image",cv2.WINDOW_AUTOSIZE)
sobel(src)cv2.waitKey(0)
cv2.destroyAllWindows()

效果图如下：
在这里插入图片描述

三、Scharr算子(Sobel算子的增强版)，但对噪声更加敏感

import cv2
import numpy as np
from matplotlib import pyplot as pltdef sobel(image):grad_x = cv2.Scharr(image,cv2.CV_32F,1,0)grad_y = cv2.Scharr(image,cv2.CV_32F,0,1)gradx = cv2.convertScaleAbs(grad_x)grady = cv2.convertScaleAbs(grad_y)cv2.imshow("gradient-x",gradx)cv2.imshow("gradient-y",grady)gradxy = cv2.addWeighted(gradx,0.5,grady,0.5,0)cv2.imshow("gradient",gradxy)src = cv2.imread(r"G:\Juptyer_workspace\study\opencv\opencv3\a1.jpg")
cv2.imshow("image",src)
cv2.namedWindow("image",cv2.WINDOW_AUTOSIZE)
sobel(src)cv2.waitKey(0)
cv2.destroyAllWindows()

效果图如下：
在这里插入图片描述

四、Laplacian算子(直接调用API)

import cv2
import numpy as np
from matplotlib import pyplot as pltdef lapalian(image):dst = cv2.Laplacian(image,cv2.CV_32F)lpls = cv2.convertScaleAbs(dst)cv2.imshow("lapalian",lpls)src = cv2.imread(r"G:\Juptyer_workspace\study\opencv\opencv3\a1.jpg")
cv2.imshow("image",src)
cv2.namedWindow("image",cv2.WINDOW_AUTOSIZE)
lapalian(src)cv2.waitKey(0)
cv2.destroyAllWindows()

效果图如下：
在这里插入图片描述

五、Laplacian算子(自定义卷积核)

import cv2
import numpy as np
from matplotlib import pyplot as pltdef lapalian(image):#kernel = np.array([[1,1,1],[1,-8,1],[1,1,1]])kernel = np.array([[0,1,0],[1,-4,1],[0,1,0]])dst = cv2.filter2D(image,cv2.CV_32F,kernel=kernel)lpls = cv2.convertScaleAbs(dst)cv2.imshow("lapalian",lpls)src = cv2.imread(r"G:\Juptyer_workspace\study\opencv\opencv3\a1.jpg")
cv2.imshow("image",src)
cv2.namedWindow("image",cv2.WINDOW_AUTOSIZE)
lapalian(src)cv2.waitKey(0)
cv2.destroyAllWindows()