1.预备知识
Beta分布函数是一种定义在实数区间[0,1]的特殊函数,它是二项式分布的共轭分布;与Beta分布相同,Dirichlet分布也是定义在实数区间[0,1]的概率度量函数,Dirichlet分布是多项式分布的共轭分布,Dirichlet分布的值域是Beta分布拓展到高维的情形。
对二项式分布、Beta分布、多项式分布不清楚的,可以参考以下文章:
https://www.cnblogs.com/171207xiaohutu/p/9335258.html
https://www.cnblogs.com/171207xiaohutu/p/9341681.html
2.Dirichlet分布
Dirichlet分布可以看做是分布之上的分布。如何理解这句话,我们可以先举个例子:假设我们有一个骰子,其有六面,分别为{1,2,3,4,5,6}。现在我们做了10000次投掷的实验,得到的实验结果是六面分别出现了{2000,2000,2000,2000,1000,1000}次,如果用每一面出现的次数与试验总数的比值估计这个面出现的概率,则我们得到六面出现的概率,分别为{0.2,0.2,0.2,0.2,0.1,0.1}。现在,我们还不满足,我们想要做10000次试验,每次试验中我们都投掷骰子10000次。我们想知道,骰子六面出现概率为{0.2,0.2,0.2,0.2,0.1,0.1}的概率是多少(说不定下次试验统计得到的概率为{0.1, 0.1, 0.2, 0.2, 0.2, 0.2}这样了)。这样我们就在思考骰子六面出现概率分布这样的分布之上的分布。而这样一个分布就是Dirichlet分布。
下面正式进入狄利克雷分布介绍,首先说一下这个多项分布的参数μ。在伯努利分布里,参数P就是抛硬币取某一面的概率,因为伯努利分布的状态空间只有{0,1}。但是在多项分布里,因为状态空间有K个取值,因此P变成了向量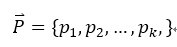 。
。
多项分布的likelihood函数形式是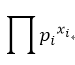 ,因此就像选择伯努利分布的共轭先验贝塔函数时那样,狄利克雷分布的函数形式应该如下:
,因此就像选择伯努利分布的共轭先验贝塔函数时那样,狄利克雷分布的函数形式应该如下: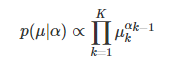
(这里的μ相当于上面的p)。上式中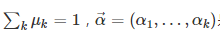 :是迪利特雷参数,把上式归一化为真正的迪利特雷分布为:
:是迪利特雷参数,把上式归一化为真正的迪利特雷分布为:
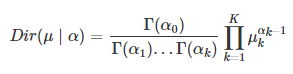
其中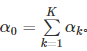
参考:https://blog.csdn.net/deropty/article/details/50266309
https://blog.csdn.net/yongheng5871/article/details/51405817
:完成一个简单的游戏)






![[HNOI2012]排队](http://pic.xiahunao.cn/[HNOI2012]排队)

)



函数)

![android paint 圆角 绘制_[BOT] 一种android中实现“圆角矩形”的方法](http://pic.xiahunao.cn/android paint 圆角 绘制_[BOT] 一种android中实现“圆角矩形”的方法)


)
