暑假第十五测

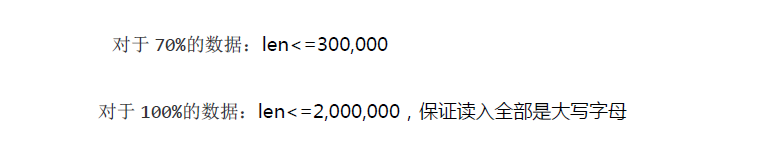
题解：

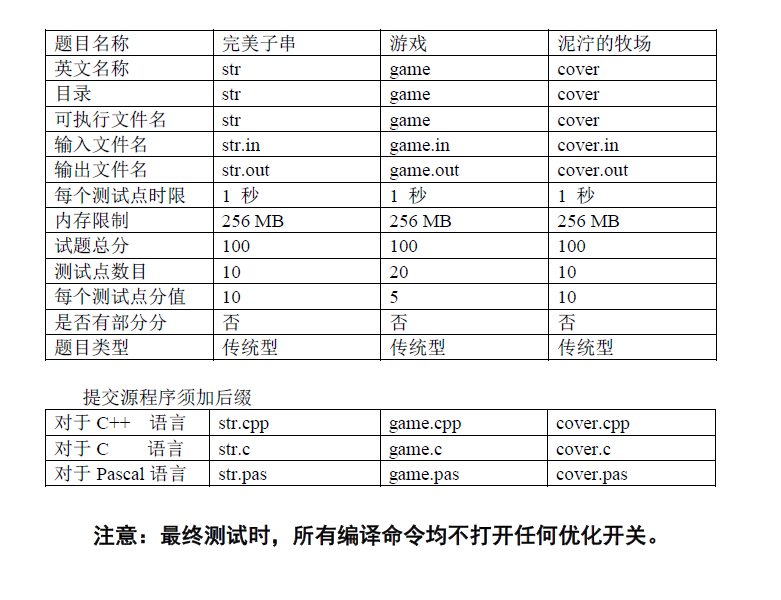
第一题：

20%枚举长度和每个子串，O（len）判断，随机情况复杂度可过

40%同样枚举长度，然后两个指针卡出区间，O(1)[或O(26)//可能可过？]判断

50%既然知道了40%的做法那么我们可以二分长度就好了

70%二分，需要O(1)判断

100%两个指针维护一个区间，保证左端点固定时，是最小的完美子串

开桶记录每个出现多少次，当一个点新加入或消失时，tot对应改变，tot=26时，更新答案，复杂度O(n)

#include<bits/stdc++.h>
using namespace std;
const int M = 2e6 + 10;
char a[M];
int len, s[M], vis[28];bool check(int k){int ret = 0;memset(vis, 0, sizeof(vis));for(int i = 1; i <= k; i++){if(!vis[s[i]])ret++;vis[s[i]]++;}if(ret >= 26)return 1;for(int i = k + 1; i <= len; i++){vis[s[i - k]]--;if(!vis[s[i - k]])ret--;if(!vis[s[i]])ret++;vis[s[i]]++;if(ret >= 26)return 1;}return 0;
}int main(){freopen("str.in","r",stdin);freopen("str.out","w",stdout);scanf("%s", a);len = strlen(a);if(len < 26){printf("QwQ\n");return 0;}for(int i = 0; i < len; i++)s[i + 1] = a[i] - 'A';int lf = 26, ans = 0, rg = len;while(lf <= rg){int mid = (lf + rg) >> 1;if(check(mid))ans = mid, rg = mid - 1;else lf = mid + 1;}if(!ans)printf("QwQ\n");else printf("%d\n",ans);
}

View Code

第二题：

将两个数相乘，看一看是不是一个数的立方，我们可以把游戏压缩成两局，变成X1^1 * X2^1 * …… * Yn-1 ^2 * Yn^2 X1 ^ 2 * X2 *^ 2 * ……* Yn-1 ^ 1 * Yn ^1, 所以他一定是一个数k的三次方；再看拆出来的k是不是x, y 的因数

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 1;
#define ll long long
ll x, y;
bool check(){ll tmp = x * y;ll lf = 1, ans = 0, rg = min(sqrt(tmp), 1e6);while(lf <= rg){ll mid = (lf + rg) >> 1;ll cc = mid * mid * mid;if(cc == tmp) {ans = mid; return (x % mid == 0 && y % mid == 0);}if(cc < tmp)lf = mid + 1;else rg = mid - 1; }return 0;
}
int main(){freopen("game.in","r",stdin);freopen("game.out","w",stdout);int T;scanf("%d", &T);while(T--){scanf("%I64d%I64d", &x, &y);if(check())puts("Yes");else puts("No");}
}

View Code

第三题：

不能盖住好地，那么宽为1的木板只能放在行、列连通块里。

•所以行、列连通块对应左、右部中的点，泥地对应边。

•求二分图最小覆盖就是答案。

二分图最小点覆盖==最大匹配

#include<bits/stdc++.h>
using namespace std;
const int M = 101;char c[M][M];
int mp[M][M];
bool vis[M*M*2];
int head[M*M*2], h[M][M], r[M*M*2], l[M][M], lf[M*M], num, tot, match[M*M*2];
struct edge{int v, nxt;}G[M*M*2];
void add(int u, int v){G[++tot].nxt = head[u]; head[u] = tot; G[tot].v = v;}bool find(int u){for(int i = head[u]; i; i = G[i].nxt){int v = G[i].v;if( !vis[v] ){vis[v] = 1;if(!match[v] || find(match[v])){match[v] = u; return 1;}}}return 0;
}int main(){freopen("cover.in","r",stdin);freopen("cover.out","w",stdout);int R, C, ans = 0, cnt = 0;scanf("%d%d", &R, &C);for(int i = 1; i <= R; i++)scanf("%s", c[i]);for(int i = 1; i <= R; i++)for(int j = 0; j < C; j++){if(c[i][j] =='*')mp[i][j + 1] = 1;//, id[i][j + 1] = ++num;
        }for(int i = 1; i <= R; i++)for(int j = 1; j <= C; j++){if(!h[i][j]){++num;for(int k = j; k <= C && mp[i][k]; k++){h[i][k] = num; //add(id[i][k], num);
                }}if(!l[i][j]){++num;for(int k = i; k <= R && mp[k][j]; k++){l[k][j] = num; //add(id[k][j], num);
                }}}for(int i = 1; i <= R; i++)for(int j = 1; j <= C; j++)if(mp[i][j]){add(h[i][j], l[i][j]);if(!r[h[i][j]]){lf[++cnt] = h[i][j];r[h[i][j]] = 1;}}for(int i = 1; i <= cnt; i++){memset(vis, 0, sizeof(vis));if(find(lf[i]))ans++;}printf("%d\n", ans);
}