[蓝桥杯]ALGO-185.算法训练_Trash Removal

 

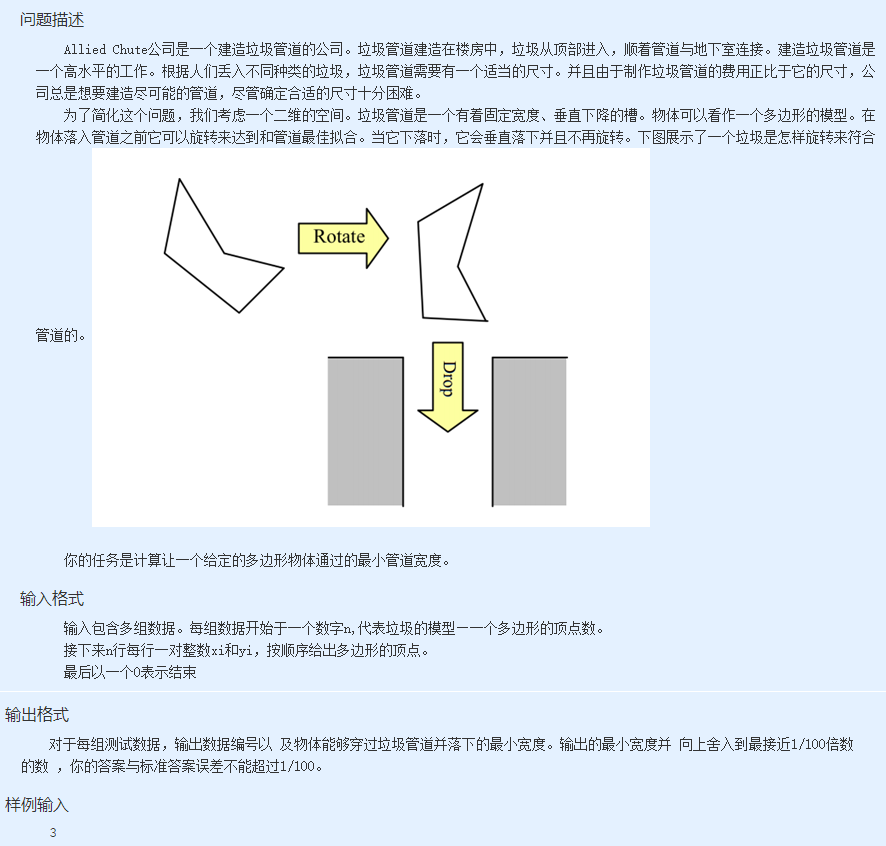
题目描述：

 

代码如下：

 

#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <iostream>
#define INF 0x7fffffff
using namespace std;
 
typedef long long LL;
const int N = 1000 + 10;
const double PI = acos(-1.0);
const double esp = 1e-10;
 
int dcmp(double x) {if(fabs(x) < esp) return 0; else return x<0?-1:1;}
 
struct Point
{
    double x,y;
    Point(double x=0,double y=0):x(x),y(y){ }
};
 
typedef Point Vector;
 
Vector operator + (Vector A, Vector B) {return Vector(A.x+B.x, A.y+B.y);}
Vector operator - (Vector A, Vector B) {return Vector(A.x-B.x, A.y-B.y);}
Vector operator * (Vector A, double p) {return Vector(A.x*p, A.y*p);}
Vector operator / (Vector A, double p) {return Vector(A.x/p, A.y/p);}
bool operator < (const Point& a, const Point& b){ return a.x<b.x || (a.x==b.x && a.y<b.y);}
bool operator == (const Point& a, const Point& b){return dcmp(a.x-b.x)==0 && dcmp(a.y-b.y)==0;}
 
double Dot(Vector A, Vector B){ return A.x*B.x+A.y*B.y; }
double Length(Vector A){return sqrt(Dot(A, A));}            //计算向量的模 
double Angle(Vector A, Vector B) {return acos( Dot(A, B)/Length(A)/Length(B) );}//计算两向量的角度 
 
double Cross(Vector A, Vector B) { return A.x*B.y - A.y*B.x ;}        //计算两向量的叉积 
double Area2(Point A, Point B, Point C){return Cross(B-A, C-A); }    //三点形成的两向量 
 
double DistanceToLine(Point P, Point A, Point B)    //计算以AB为底边的高 
{
    Vector v1 = B-A, v2 = P-A;
    return fabs(Cross(v1, v2)) / Length(v1);
}
int ConvexHull(Point *p, int n, Point *ch)
{
    sort(p,p+n);    //排序各顶点 
    int m = 0;
    for(int i=0;i<n;i++)    //维护凸壳 
    {
        while(m>1 && Cross(ch[m-1]-ch[m-2], p[i]-ch[m-2]) <= 0) m--;
        ch[m++] = p[i];        //记录凸壳的顶点 
    }
    int k = m;    //记录凸壳顶点数 
    for(int i = n-2 ;i>=0;i--)    //除去底边的两个顶点 
    {
        while(m>k && Cross(ch[m-1]-ch[m-2], p[i]-ch[m-2]) <= 0) m--;
        ch[m++] = p[i];
    }
    if(n > 1) m--;
    return m;
}
 
int n;
Point P[N],ch[N];
 
int main()
{
    int C=1;
    while(scanf("%d",&n)!=EOF && n)    //输入多边形的边数 
    {
        for(int i=0;i<n;i++)
        {
            scanf("%lf%lf",&P[i].x,&P[i].y);//记录各点的坐标 
        }
        int m=ConvexHull(P,n,ch);    //得到该多边形的凸壳顶点数 
        double ans = 1e20;            //用于记录最小宽度 
        for(int i=1;i<=m;i++)        //枚举凸壳的顶点 
        {
            double max_dis = 0;        //用于记录各底边的高 
            for(int j=0;j<m;j++)    //确定底边后，查找其对应的高，并记录最大值 
            {
                max_dis = max(max_dis, DistanceToLine(ch[j],ch[i%m],ch[i-1]));
            }
            ans = min(ans, max_dis);//最小宽度即为最大高度 
        }
        ans = ceil(ans * 100) / 100.0;
 
        printf("Case %d: %.2lf\n",C++, ans);
    }
 
    return 0;
}

 

 

解题思路：

该题使用了几何计算中的凸边算法（什么是凸边：https://blog.csdn.net/HouszChina/article/details/79251474）

首先对输入多边形的点进行凸壳维护，得到凸壳的点集

然后枚举底边，计算对应的高，并保留最大的高度(即题目要求的最小宽度)