前面几篇我们介绍的都是线性支持向量机，换句话说，我们总可以用一条线或一个超平面将数据进行分割。如下图所示：

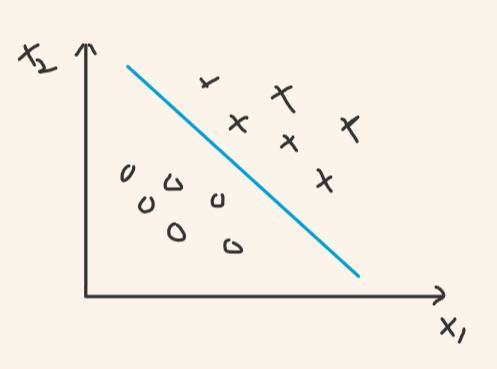
但在更多情况下，有些数据是无法进行线性分割的。比如下面的例子：

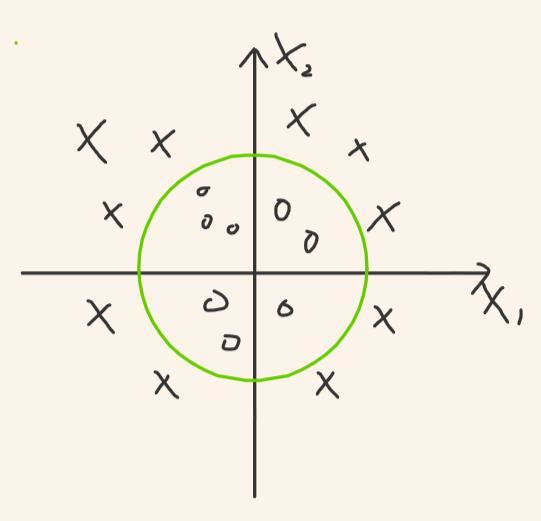
也就是说，你永远无法用一条直线将两类数据分开，你只能用一个圆来实现。这就是非线性分割。

那么具体到SVM模型中，这种非线性分割的情况我们就用“核函数”来进行处理。

核函数

首先，在SVM中，我们将原始优化问题转化成了它的对偶问题，即

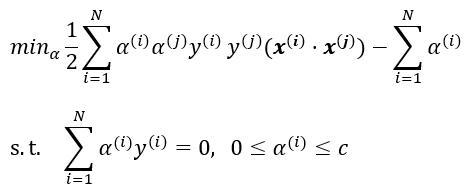
注意到，在上面的式子中，我们的特征是以向量点积的形式出现。

对于非线性的情况，我们通常是用一个映射函数将特征从低维空间映射到高维空间中，从而实现线性可分。

用公式表示为：

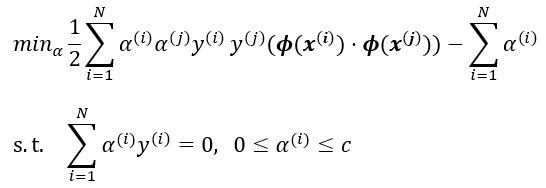
但是在SVM中，我们并没有使用这种方法。因为寻找这样的映射函数很困难，而且计算量极大。

SVM使用了另一种方式来实现，这就是“核函数”。它通过将向量的内积x1·x2转换为核函数K(x1·x2)，即

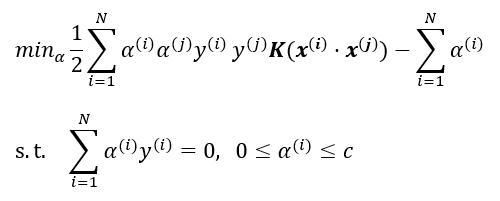
同时，我们的决策函数也要做相应的替换，即

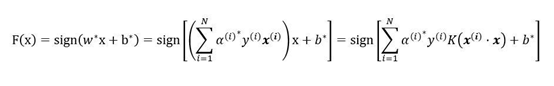
核函数类型

常用的核函数主要有以下几类：

1.线性核函数

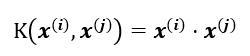
2.高斯核函数

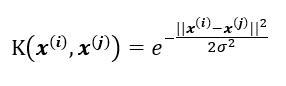
3.多项式核函数

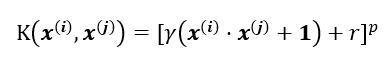
4.sigmoid核函数

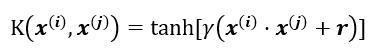
UA学院招生啦！想打造AI时代底层能力的同学请看过来！