牛顿法(Newton method)和拟牛顿法(quasi-Newton method)也是求解无约束最优化问题的常用方法,具有收敛速度快的优点。
牛顿法是迭代算法,每一步需要求解目标函数的海赛矩阵的逆矩阵,计算比较复杂。
拟牛顿法通过正定矩阵近似海赛矩阵的逆矩阵或海赛矩阵,简化了这一计算过程。
本篇设计的算法有:牛顿法、拟牛顿法、DFP算法、BFGS算法、L-BFGS算法、Broyden类算法。
1.牛顿法
对于一个无约束问题:
我们知道,通常情况下对于目标函数来说,极小值点的一阶导数为0。
而
其中,
那么函数的一阶导数(对上面的二阶泰勒展开求导)就可以表示为:
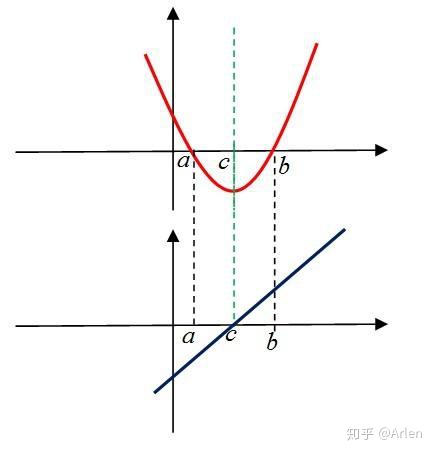
上式就是我们的一阶导函数的直线近似,即上式为通过原函数的一阶导函数在点
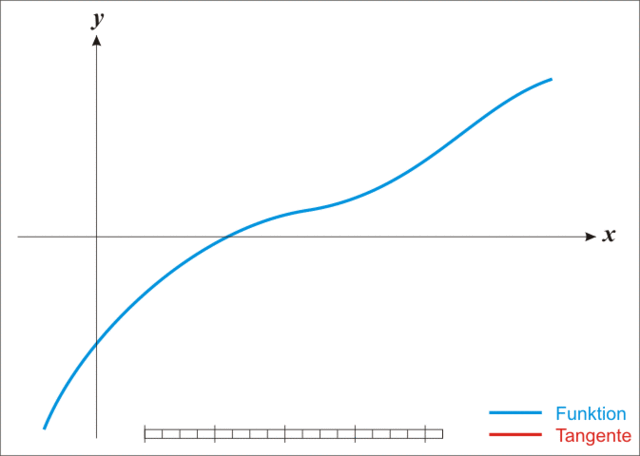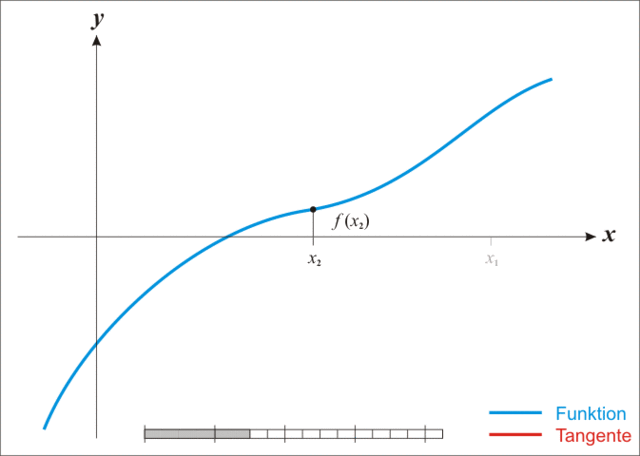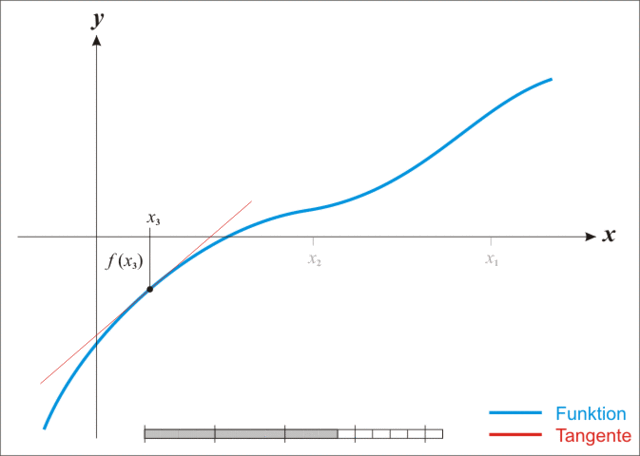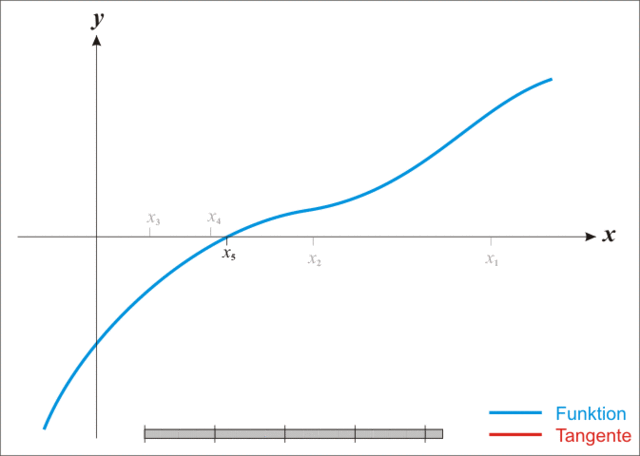
如上图所示,已知第
我们令其为0得到:
从而解得第
这个就是牛顿法!
但是我们可以看见在每一次的迭代过程中,都要涉及到
来说一次,这就是牛顿法!!
牛顿法的迭代公式中由于没有步长因子,是定步长迭代,对于非凸目标函数,有时会使函数值上升,即出现
牛顿法的一些致命缺点:
1.海赛矩阵的逆矩阵计算
2.海赛矩阵可能无法保持正定,这样就无法计算
这时我们就应该思考了,能不能绕过
2.拟牛顿法
拟牛顿法的基本思想是:不用求二阶偏导数而构造出可以近似海赛矩阵(或海赛矩阵的逆)的正定对称阵。
不同的构造方法对应能够产生不同的拟牛顿法。(可以理解成,"拟牛顿法"是来近似"牛顿法"的,所以在“牛顿法”前面加了一个“拟”字。拟牛顿法可不止一种,它包含多种方法:如DFP算法、BFGS算法、Broyden类算法。)
我们说了,我们要构造一个近似海赛矩阵(或海赛矩阵的逆)的正定矩阵,首先需要满足拟牛顿条件。
(1)拟牛顿条件
对
假设找到了下一步迭代点
记
上述就是拟牛顿条件,即我们选择的
从拟牛顿条件我们可知,有两种替补方式:
1)选择
2)选择
(2)DFP算法
DFP算法用
可以证明,如果初始矩阵
此时有个疑问,计算
这就绕过了
可以对照算法过程来理解,DFP算法过程如下:
输入:目标函数
输出:
1)选定初始点
2)计算
3)置
4)一维搜索:求
5)置
6)计算
7)置
(3)BFGS算法
BFGS算法是最流行的你牛顿算法。它与DFP相比,性能更佳。该算法是用
同DFP算法,也可以证明,如果初始矩阵
BFGS的算法流程与DFP相似,如下:
输入:目标函数
输出:
1)选定初始点
2)计算
3)由
4)一维搜索:求
5)置
6)计算
7)置
上述就是具体地算法过程了,当然,我们也可以从BFGS算法矩阵
首先我们介绍Sherman-Morrison公式(谢尔曼莫里森公式):假设
这就是Sherman-Morrison公式。
如果我们记
即称此式为BFGS算法关于
(4)L-BFGS算法
在BFGS算法中,每一步迭代都需要用到一个
L-BFGS算法就是为了解决这个问题而提出的,其目的是减少BFGS算法迭代过程中所需的内存开销。
L-BFGS(Limited-memory BFGS或Limited-storage BFGS)是BFGS算法的进一步近似。其基本思想是:不再存储完整的矩阵
(5)Broyden类算法
根据前面的内容,我们将由DFP算法中
也满足拟牛顿条件而且是正定的。其中
这样,根据取不同的
上面的所有拟牛顿算法都仅仅是简述,例如DFP和BFGS算法的迭代公式没有推导其由来,L-BFGS算法也仅仅是提了一下。如果需要深入理解,可以参考下面的这个博客链接:
https://blog.csdn.net/songbinxu/article/details/79677948



















