💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
文献来源:

压缩传感(CS)是最近出现的技术,也是信号和图像处理中广泛研究的问题,它提出了一种新的框架,用于以明显低于奈奎斯特速率的速率同时采样和压缩稀疏或可压缩信号。也许,设计一个反映图像稀疏先验信息的有效正则化项在CS图像恢复中起着至关重要的作用。近年来,局部平滑度和非局部自相似性都导致了CS图像恢复的先验稀疏性。本文首先,建立了自适应曲线阈值判据,试图自适应去除CS恢复过程中恢复图像中出现的扰动,强加稀疏性。此外,还建立了一种新的稀疏性度量,称为联合自适应稀疏性正则化(JASR),该度量在变换域中同时强制执行局部稀疏性和非局部三维稀疏性。然后,提出了一种基于JASR的高保真CS图像恢复技术——CS-JASR。为了有效地求解所提出的相应优化问题,我们采用了拆分布雷格曼迭代。大量的实验结果证明了与目前最先进的CS图像修复方法相比,所提方法的充分性和有效性。
原文摘要:
Compressive sensing (CS) is a recently emerging technique and an extensively studied problem in signal and image processing, which suggests a new framework for the simultaneous sampling and compression of sparse or compressible signals at a rate significantly below the Nyquist rate. Maybe, designing an effective regularization term reflecting the image sparse prior information plays a critical role in CS image restoration. Recently, both local smoothness and nonlocal self-similarity have led to superior sparsity prior for CS image restoration. In this paper, first, an adaptive curvelet thresholding criterion is developed, trying to adaptively remove the perturbations appeared in recovered images during CS recovery process, imposing sparsity. Furthermore, a new sparsity measure called joint adaptive sparsity regularization (JASR) is established, which enforces both local sparsity and nonlocal 3-D sparsity in transform domain, simultaneously. Then, a novel technique for high-fidelity CS image recovery via JASR is proposed-CS-JASR. To efficiently solve the proposed corresponding optimization problem, we employ the split Bregman iterations. Extensive experimental results are reported to attest the adequacy and effectiveness of the proposed method comparing with the current state-of-the-art methods in CS image restoration.
📚2 运行结果
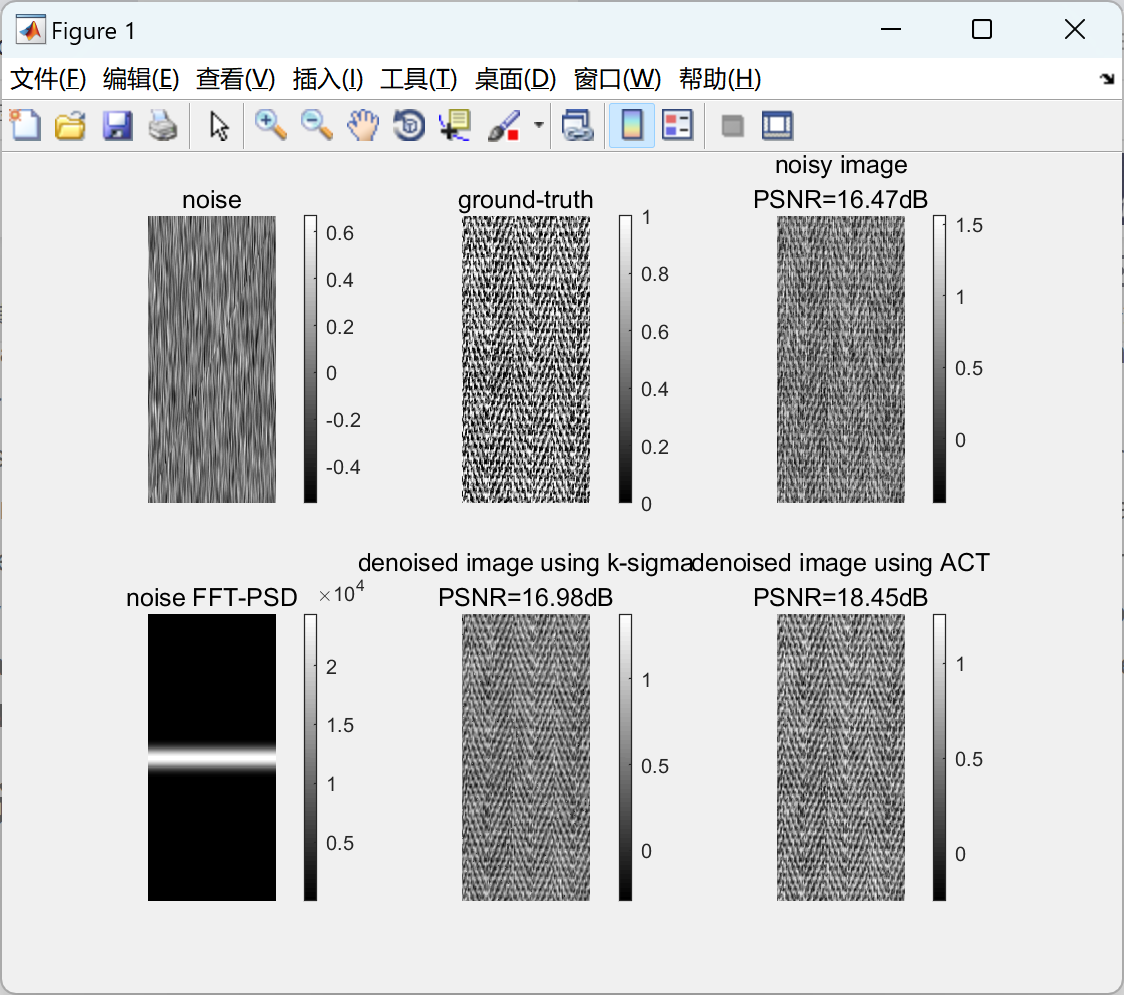
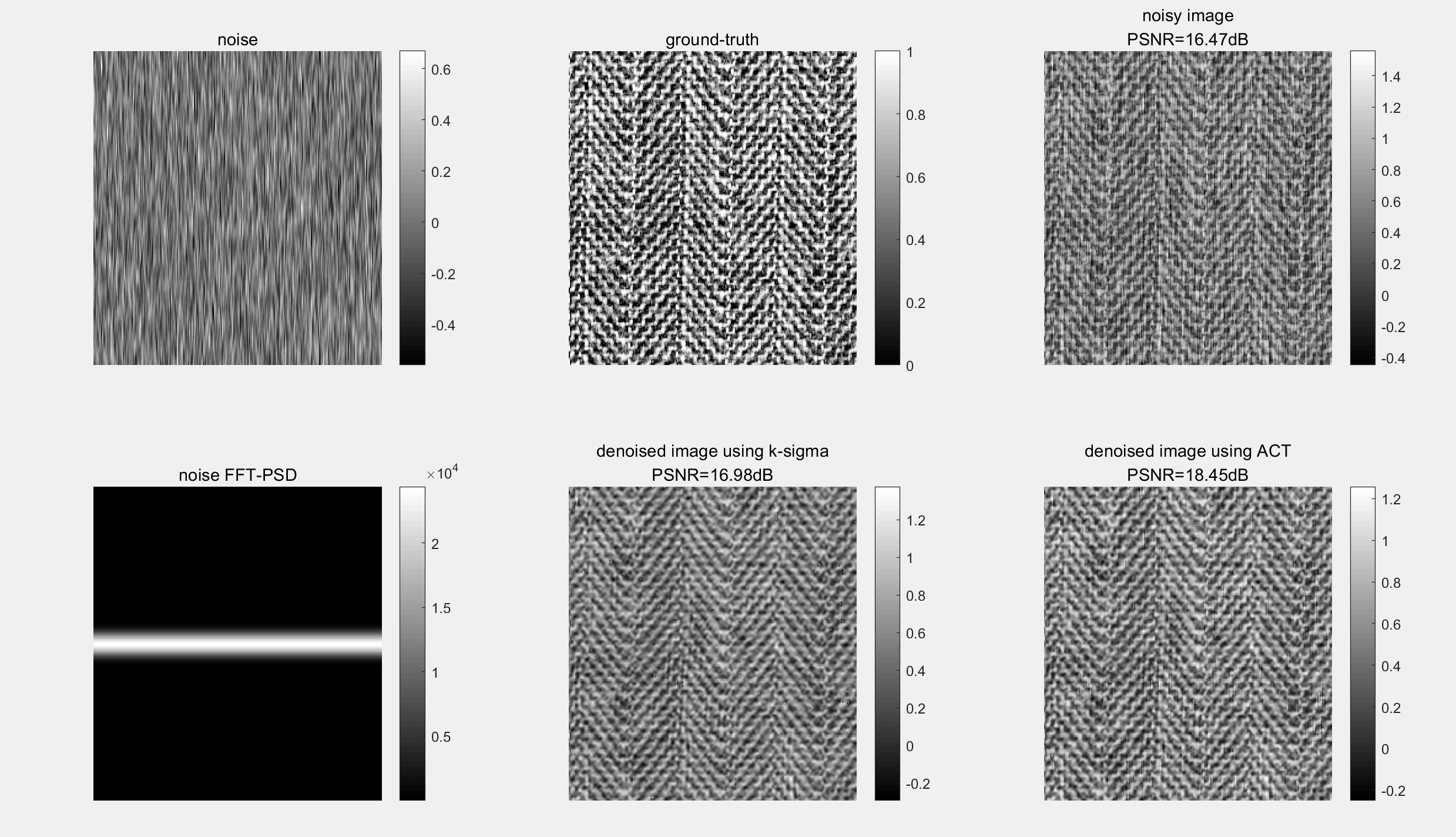
可视化代码:
%%% displaying the images
figure,
subplot(2,3,1), imagesc(noise), colormap('gray'),
colorbar, title('noise'), axis off
subplot(2,3,4), imagesc(fftshift(noise_FFT_PSD)), colormap('jet'),
colorbar, title('noise FFT-PSD'), axis off
subplot(2,3,2), imagesc(x), colormap('gray'),
colorbar, title('ground-truth'), axis off
subplot(2,3,3), imagesc(z), colormap('gray'),
colorbar, axis off, title(sprintf('noisy image\nPSNR=%0.2fdB',psnr_noisy))
subplot(2,3,5), imagesc(x_est_ksigma), colormap('gray'),
colorbar, axis off, title(sprintf('denoised image using k-sigma\nPSNR=%0.2fdB',psnr_ksigma))
subplot(2,3,6), imagesc(x_est_ACT), colormap('gray'),
colorbar, axis off, title(sprintf('denoised image using ACT\nPSNR=%0.2fdB',psnr_act))
%% Auxiliary function for generating Gaussian noise
function [noise, noise_FFT_PSD] = generate_Gaussian_noise(SizeX)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% generate_Gaussian_noise creates stationary white/colored Gaussian noise
% with respect to a convolutional kernel selected randomly.
%
%
% FUNCTION INTERFACE:
% [noise, noise_FFT_PSD] = generate_Gaussian_noise(SizeX)
%
% ________________________________________________________________________________
% INPUT: | CLASS: | DESCRIPTION:
% --------------------------------------------------------------------------------
% SizeX | (double) | Size of the ground-truth image.
%
%
% ________________________________________________________________________________
% OUTPUTS: | CLASS: | DESCRIPTION:
% --------------------------------------------------------------------------------
% noise | (double) | generated stationary Guassian noise.
% --------------------------------------------------------------------------------
% noise_FFT_PSD | (double) | the noise FFT-PSD (as size as SizeX).
%
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
kernel_type = randi([1 14]); % the randomly selected kernel for noise generation
normalizer = @(n) (n-mean(n(:)))./std(n(:)); % making the noise zero-mean with unit variance
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。

Compressive Sensing Image Restoration Using Adaptive Curvelet Thresholding and Nonlocal Sparse Regularization | IEEE Journals & Magazine | IEEE Xplore



{编写demo程序})

)




)


漏洞复现与分析容器逃逸)





— 手把手教你如何去划分数据集)
