进制

23678(10进制） = 2*10000+3*1000+6*100+7*10+8*1= 2*10^4 + 3*10^3 + 6*10^2 + 7*10^1 + 8*10^0= 23678

如上例所示，10 称做"基数"，10^n(10 的 n 次幂，n从0开始)被称作"权"，10000 1000 100 10 1

2进制的基数为2，权为2^n(2的n次方)，128 64 32 16 8 4 2 1

16进制的基数为16，权为 16^n(16的 n 次方)，4096 256 16 1

P.S 16进制的前缀是0X，数字零和英文字母X；

8进制的基数为8，权为 8^n(8的 n 次方)，512 64 8 1

P.S 8进制的前缀通常是数字0。

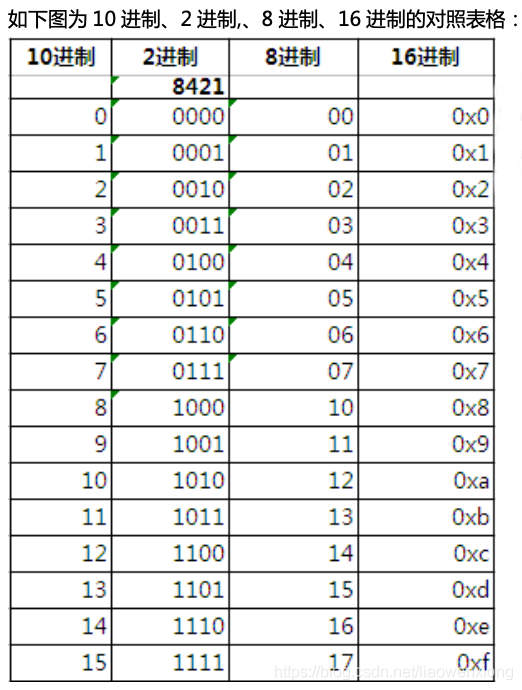
注意：10进制与其它进制的转换不能直接通过对照表的对应关系做简单的替换，没有这样的替换关系

进制转换

二进制和十进制互相转换

十进制 → 二进制

十进制正整数 → 二进制

方法一（辗转减权法）

十进制数：3765，如何转换成二进制数？

第一步，写出二进制的权数如下：

第十二位	第十一位	第十位	第九位	第八位	第七位	第六位	第五位	第四位	第三位	第二位	第一位
2048	1024	512	256	128	64	32	16	8	4	2	1

注意：权数是以十进制数来表示的，相邻数是两倍的关系，最大的权数必须最接近被转换的十进制数（3765）

第二步，计算下3765含有多少个二进制的权数

3765 - 2048 = 1717，表示含有1个2048；
1717 - 1024 = 693， 表示含有1个1024；
693 - 512 = 181， 表示含有1个512；
181 - 128 = 53， 表示含有1个128；
53 - 32 = 21， 表示含有1个32；
21 - 16 = 5， 表示含有1个16；
5 - 4 = 1， 表示含有1个4；
1 - 1 = 0， 表示含有1个1。

那么我们按二进制的权数位置来标数，如下：

\	第十二位	第十一位	第十位	第九位	第八位	第七位	第六位	第五位	第四位	第三位	第二位	第一位
权数	2048	1024	512	256	128	64	32	16	8	4	2	1
二进制数	1	1	1	0	1	0	1	1	0	1	0	1

结果：十进制数3765转换成二进制数是：1110101110101，计算机默认按int类型保存，所以实际应该是32位的二进制数：
00000000 00000000 00001110 10110101

方法二（辗转整除法/除2取余法）

叫「辗转整除法」，十进制数转换成二进制数，那么就除以2，必须整除，得到“商数”继续除以2，直到“商数”为0，最后得到的余数逆序排列就是对应的二进制数了。也叫「除2取余，逆序排列法」。

十进制数：12，如何转成二进制数？

说明：12 ➗ 2 = 6，余数0；6 ➗ 2 = 3，余数0；3 ➗ 2 = 1，余数1；1➗ 2 = 0，余数1

十进制负整数 → 二进制

-33转成二进制

思路：先得到33的二进制数，然后取反+1得到-33的二进制数

如果转成8位的二进制补码，计算过程如下：

1. 33的二进制补码：0010 0001
2. 取反得：1101 1110
3. +1得：1101 1111

最后得到-33的8位二进制码：1101 1111

十进制负小数 → 二进制

-0.98如何转换成二进制

思路：
先得到0.98的二进制数，然后取反+1得到-0.98的二进制数

0.98通过乘2取整法，得到二进制数。

十进制小数 → 二进制

十进制小数转换成二进制小数采用"乘2取整，顺序排列"法。具体做法是：用2乘十进制小数，可以得到积，将积的整数部分取出，再用2乘余下的小数部分，又得到一个积，再将积的整数部分取出，如此进行，直到积中的小数部分为零，或者达到所要求的精度为止。
然后把取出的整数部分按顺序排列起来，先取的整数作为二进制小数的高位有效位，后取的整数作为低位有效位。

例如：0.96875如何转换成二进制

二进制 → 十进制

二进制负整数 → 十进制

二进制数：11011111，如何转成十进制数呢？

前提是要确认11011111是不是八位的二进制数（即byte类型），如果是byte类型，那么11011111肯定是负数，第一位表示符号，第一位为1表示负数，所以不能直接转换成十进制数，需要先得到正数的补码，再转换成十进制的正数，最后得到对应的负数。

第一步，先得到正数的补码（即负数对应的正数的二进制数）：
取反+1
11011111

\	二进制数
负数	11011111
取反	00100000
+1得到补码	00100001

最后得到11011111对应的正数的补码：00100001

第二步，正数补码转换成十进制数

就是二进制数和对应的位置的权数相乘，最后求和，就可以得到十进制数。这个叫「按权相加法」。
换个表述，正的二进制整数，第n位置的数乘以2^(n-1)，最后求和，就可以得到十进制数。n由右到左，从1开始。

\	第八位	第七位	第六位	第五位	第四位	第三位	第二位	第一位
权数	128	64	32	16	8	4	2	1
二进制数	0	0	1	0	0	0	0	1

十进制数：0 * 128 + 0 * 64 + 1 * 32 + 0 * 16 +0 * 8 + 0 * 4 + 0 * 2 + 1 * 1 = 33

第三步，既然11011111对应的十进制正数是33，那么11011111对应的十进制负数就是-33

说明：

1. 所谓补码，其实就是二进制数，需遵循特定的二进制运算规则（即在封闭的位数范围内运算，举例：1111+0001 = 10000，若按4位补码运算，要把1舍弃，才能得到正确的结果0000，对照「二进制补码表」可知，计算结果正好和十进制的-1+1=0的运算结果一致）；
2. 计算机中正的二进制数和负的二进制数的关系是取反+1。例如：二进制八位补码00000111（7），对应的负数补码就是对正数的二进制数（也就是补码）取反+1，得到11111001（-7）。而二进制负数11111001对应的二进制正数，也是对负数11111001取反＋1得到00000111；
3. 计算机内部数据是以二进制补码来表示；
4. 补码的负数最高位是1，补码的正数最高位是0，最高位也称为“符号位”。

二进制的正整数 → 十进制

二进制数：11011111，如何转成十进制数呢?

前提是要确认这个二进制数的类型，如果是byte类型按上述流程来进行转换，如果是short（16位），int（32位），long（64位）等类型的，那么说明前面都是0，给省略了，说明是正数，可以直接转换成十进制数，也就是才有「按权相加法」得到十进制数。

\	第八位	第七位	第六位	第五位	第四位	第三位	第二位	第一位
权数（位权）	128	64	32	16	8	4	2	1
二进制数	1	1	0	1	1	1	1	1

十进制数：1 * 128 + 1* 64 + 0 * 32 + 1 * 16 +1 * 8 + 1 * 4 + 1 * 2 + 1 * 1 = 223

二进制小数 → 十进制

二进制的小数位则从左向右开始算，依次列为第1、2、3………n，然后将第n位的数乘以2的-n次方，然后相加即可得到小数位的十进制数（按权相加法）。

111.01如何转换成十进制数？

将二进制数据111.01写成加权系数的形式:
1 * 2²+ 1 * 2¹+1 * 2⁰ + 0 * 2^-1 + 1 * 2^-2 = 7.25
答：二进制111.01 转换成十进制7.25

0.11111，如何转换成十进制数呢？

1 * 2^-1 + 1 * 2^-2 + 1 * 2^-3 + 1 * 2^-4 + 1 * 2^-5 = 0.96875
答：二进制0.11111转换成十进制0.96875

二进制的负小数 → 十进制

思路：
通过二进制的负小数取反+1得到对应的二进制的正小数，然后计算出正小数的十进制数，最后看得到对应的十进制负数，这个负数就是二进制负小数转换十进制的结果值。

八进制和十进制的转换

Octal，缩写OCT或O，一种以8为基数的计数法，采用0，1，2，3，4，5，6，7八个数字，逢八进1。一些编程语言中常常以数字0开始表明该数字是八进制。八进制的数和二进制数可以按位对应（八进制一位对应二进制三位），因此常应用在计算机语言中。

十进制 → 八进制

十进制正整数 → 八进制

方法一：叫「辗转整除法」，也叫「除8取余法」
十进制数转换成八进制数，就是拿十进制数除以8，必须整除，得到的“商数”继续除以8，直到“商数”为0，最后得到的余数逆排序就是对应的8进制数了。

将十进制数115转化为八进制数

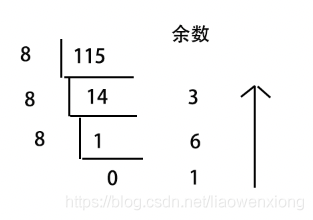
结果：（115）10 = （163）8

方法2：先将十进制数转换成二进制数，再将二进制数化为八进制数

十进制数115转换成八进制数是多少呢？

（115）10 = （1110011）2 = （001 110 011）（163）8

十进制数-2转换成八进制是多少呢？

先得到2的二进制数：00000000000000000000000000000010
取反+1得到-2的二进制数：11111111111111111111111111111110
转换为8进制 ：37777777776

十进制负整数 → 八进制

思路：
十进制负数 → 二进制数 → 八进制

-2 的二进制数：11111111 11111111 11111111 1111110
转成八进制：37777777776

十进制小数 → 八进制

将十进制数（0.3125）10转换成八进制数。

「乘8取整法」

十进制小数转换成八进制小数采用"乘8取整，顺序排列"法。具体做法是：用8乘十进制小数，可以得到积，将积的整数部分取出，再用8乘余下的小数部分，又得到一个积，再将积的整数部分取出，如此进行，直到积中的小数部分为零，或者达到所要求的精度为止。
然后把取出的整数部分按顺序排列起来，先取的整数作为八进制小数的高位，后取的整数作为低位，这样由各整数部分组成的数字就是转化后八进制小数的值。

0.3125x8 = 2 .5 2
0.5x8 = 4 .0 4
结果：（0.3125）10=（0.24）8

十进制的负小数 → 八进制

思路：
先得到对应的十进制正小数，十进制的正小数转成二进制的正小数，再取反+1得到二进制的负小数，这个就是十进制的负小数转换成二进制的结果，然后把二进制负小数，三对一换成八进制数值即可。

八进制 → 十进制

八进制的正整数 → 十进制

就是八进制数和对应的位置的权数相乘，最后求和，就可以得到十进制数。这个叫「按权相加法」。
8进制的权数：8⁰，8¹，8² ……

将八进制数12转换成十进制数

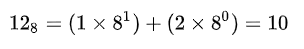
将八进制数（751）8转换成十进制数

（751）8=（7x8²+5x8¹+1x8⁰）10=（448+40+1）10=（489）10

八进制的小数 → 十进制数

小数位则从左向右开始算，依次列为第1、2、3………n，然后将第n位的数乘以8的-n次方，然后相加即可得到小数位的十进制数（按权相加法）。

八进制的0.16转换成十进制是多少？

（0.16）8=（1x8^-1+6x8^-2）10=（0.125+0.09375）10=（0.21875）10

P.S 括号外的数字是注释是多少进制的数，本来是应该打底标，但是CSDN不行

八进制的负整数 → 十进制

思路：
八进制负数转成二进制数，再转成十进制数

(37777777776) 8 = (11 111 111 111 111 111 111 111 111 111 110) 2

对11111111 11111111 11111111 1111110
取反+1，得到对应的正数补码：
00000000 00000000 00000000 00000010 ，而这个正数补码对应的十进制是2，所以11111111 11111111 11111111 1111110 对应的十进制数是-2，最后得到(37777777776) 8对应的十进制是-2

八进制的负小数 → 十进制

思路：
八进制负小数转成二进制负小数，取反+1得到二进制正小数，再得到十进制的正小数，再得到十进制的负小数，这个十进制负小数就是八进制负小数转换成十进制的结果值

十六进制和十进制的转换

十六进制 → 十进制

十六进制正整数 → 十进制

将十六进制数（A7）16转换成十进制数

「按权相加法」

十六进制的权数（从右到左）：16⁰，16¹，16²…

（A7）16=（10x16¹+7x16⁰）10=（160+7）10=（167）10

0x7fbe转成十进制数

0x7fbe这个数是int类型，前面的0省略了，这是个正数，直接「按权相加」得到十进制数：
7 * 16³ + 15 * 16² + 11 * 16¹ +14 * 16⁰ = 32702

十六进制小数 → 十进制

以小数点为界，整数位从右向左开始算，依次列为第1、2、3………n，然后将第n位的数（0-9，A-F）乘以16的n-1次方，然后相加即可得到整数位的十进制数；小数位则从左向右开始算，依次列为第1、2、3………n，然后将第n位的数（0-9，A-F）乘以16的-n次方，然后相加即可得到小数位的十进制数（按权相加法）。

将十六进制数（0.D4）16转换成十进制数

（0.D4）16=（13x16^-1+4x16^-2）10=（0.8125+0.015625）10=（0.828125）10

十六进制负整数 → 十进制

十六进制的负数，从字面量来看，不好直接看不出来到底是负数还是正数，而如果是负数，又不能直接通过「按权相加法」计算得到十进制数，所以保险起见，最好把十六进制的数先转换成二进制数，然后通过二进制数的符号来判断是否负数。

0xffffffdf转成十进制是多少？

1. 先转成二进制：11111111 11111111 11111111 11011111
2. 再得到对应正数的二进制：00000000 00000000 00000000 00100001，转成十进制：33
3. 所以11111111 11111111 11111111 11011111对应的十进制是-33，也就是说0xffffffdf对应的十进制是-33

十六进制负小数 → 十进制

思路：
先转成二进制补码，如果确定是负数，取反+1，得到对应的正数补码，正数补码转成十进制数，这个十进制的正数加个“负号”，就是十六进制负小数转换成十进制的结果值。

十进制 → 十六进制

十进制正整数 → 十六进制

「除16取余法」：十进制数转换成十六进制数，就是拿十进制数除以16，必须整除，得到的“商数”继续除以16，直到“商数”为0，最后得到的余数逆排序就是对应的16进制数了。

将十进制数（93）10转换成十六进制数

93/16=5………13（D）

5/16 = 0… … 5

（93）10=（5D）16

十进制小数 → 十六进制

「乘16取整法」
十进制小数转换成16进制小数采用"乘16取整，顺序排列"法。具体做法是：用16乘十进制小数，可以得到积，将积的整数部分取出，再用16乘余下的小数部分，又得到一个积，再将积的整数部分取出，如此进行，直到积中的小数部分为零，或者达到所要求的精度为止。
然后把取出的整数部分按顺序排列起来，先取的整数作为16进制小数的高位，后取的整数作为低位，这样由各整数部分组成的数字就是转化后16进制小数的值。

将十进制数（0.3125）10转换成十六进制数

0.3125x16 = 5 .0

（0.3125）10=（0.5）16

十进制负小数 → 十六进制

-15.8转成十六进制是多少？

思路：
先得到-15.8的二进制数，再转成十六进制数

1. 得到15.8的二进制数：
   整数通过「除2取余法」获得，小数通过「乘2取整法」得
2. 取反+1得到-15.8的二进制数
3. 最后根据“十六进制与二进制的转换关系表”，四位为一组替换成十六进制的值

十进制负整数 → 十六进制

-33转成十六进制是多少？

十进制的负数不能通过「除以16取余法」来转换成十六进制。
必须先得到-33的二进制补码：1101 1111，最后根据“十六进制与二进制的转换关系表”，四位为一组替换成十六进制的值，最后得到结果：0xdf。但是这样的结果是正确的吗？？-33 = 0xdf 吗？？

分析下0xdf：
字面量默认是int类型，32位，而0xdf只有8位，显然是省略前面的0了，那么显然这是个正数（前面提到不好直接看出来是否负数，可以转成二进制判断是否负数），可以直接通过「按权相加法」得到对应的十进制数：0xdf = 0x000000df = 13 * 16^1^+15 * 16^0^ = 208 + 15 = 223，所以0xdf != -33。

也就是说不论是-33还是0xdf，计算机都是当成int类型的数值，所以-33转成二进制补码应该是32位的，就是：11111111 11111111 11111111 11011111，那么转成十六进制数就是：0xffffffdf。而0xdf转成二进制数是：00000000 00000000 00000000 11011111

总结：
-33计算机认为是一个int类型的数值，会以32位的二进制表示：11111111 11111111 11111111 11011111，转成十六进制就是：0xffffffdf。
0xdf计算机认为是一个int类型的数值，转成二进制是：00000000 00000000 00000000 11011111，转成十进制是：223。

实质上-33如果表示成8位的二进制补码，再转成十六进制的确是0xdf，只不过计算机不这么干，而0xdf转成8位二进制补码，再转成十进制确实是-33，只是计算机不这么干。

所以0xdf

• 对应8位的二进制补码而言，转成十进制是-33
• 对应32位的二进制补码而言，转成十进制223

所以-33

• 对应8位的二进制补码而言，转成十六进制是0xdf
• 对应32位的二进制补码而言，转成十六进制是0xffffffdf

如果要把0xdf按8位的二进制补码运算，需要强制类型转换：

byte b = (byte)0xdf;
System.out.println(b); // 结果输出 -33

二进制和八进制的转换

八进制 → 二进制

二进制与八进制的互相转换和二进制与十六进制的转换类似，区别在于需要操作的是三位一组而不是四位。下表2-2列出了二进制与八进制的等效表示。

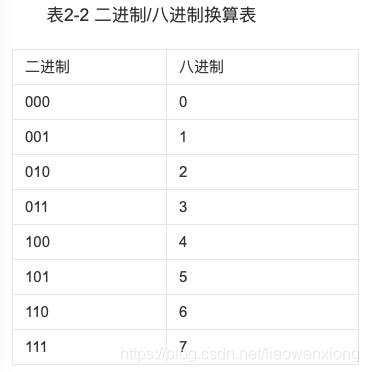
八进制正整数 → 二进制

八进制123换算成二进制的结果是多少？

为了把八进制数换算为二进制，将每一个八进制数字替换成表2-2中对应的二进制三位：

将八进制数（751）8转换成二进制数

（751）8=（7 5 1）8=（111 101 001）2=（111101001）2

八进制小数 → 二进制

8进制17.36如何转换成二进制

规则：按照顺序，每1位八进制数改写成等值的3位二进制数，次序不变。

（17.36）8 = （001 111 .011 110）2 = （1111.01111）2

将八进制数（0.16）8转换成二进制数

（0.16）8=（0. 1 6）8=（0. 001 110）2=（0.00111）2

八进制负整数 → 二进制

(37777777776) 8怎么转换成二进制

根据对照表将八进制的数逐一替换二进制数
(37777777776) 8 = (11 111 111 111 111 111 111 111 111 111 110) 2

八进制的负小数 → 二进制

思路：
根据对照表将八进制的数逐一替换二进制数即可

二进制 → 八进制

表述一：
整数部份从最低有效位开始，以3位一组，最高有效位不足3位时以0补齐，每一组均可转换成一个八进制的值，转换完毕就是八进制的整数。
小数部份从最高有效位开始，以3位一组，最低有效位不足3位时以0补齐，每一组均可转换成一个八进制的值（表2-2查找对应的八进制值），转换完毕就是八进制的小数。

表述二：
因为每三位二进制数对应一位八进制数，所以，以小数点为界，整数位则将二进制数从右向左每3位隔开，不足3位的在左边用0填补即可；小数位则将二进制数从左向右每3位隔开，不足3位的在右边用0填补即可。

二进制的正整数 → 八进制

将二进制数(10010) 2转化成八进制数是多少？

（10010）2=（010 010）2=（2 2）8=（22）8

二进制小数 → 八进制

例1：将二进制数（0.1010）2转化为八进制数。
（0.10101）2=（0. 101 010）2=（0. 5 2）8=（0.52）8

例2：将二进制数（11001111.01111）2 转化成八进制数。（11001111.01111）2 = （011 001 111.011 110）2 = （317.36）8

二进制负整数 → 八进制

16位二进制补码11111111 11110110 转换成八进制

参照表2-2，将二进制的三位替换成对应的八进制数值即可。
(1111111111110110 ) 2 = (001 111 111 111 110 110) 2 = (177766) 8

二进制的负小数 → 八进制

思路：
根据对照表将二进制的数逐一替换八进制数

二进制和十六进制的转换

二进制和十六进制的对照表

二进制 → 十六进制

因为每四位二进制数对应一位十六进制数，所以，以小数点为界，整数位则将二进制数从右向左每4位隔开，不足4位的在左边用0填补即可；小数位则将二进制数从左向右每4位隔开，不足4位的在右边用0填补即可。

二进制正整数 → 十六进制

0111 1101转成十六进制数

不要管是否负数，直接根据对照表，4个二进制数对1个十六进制数，逐一替换即可。
（0111） 2 →（7）10 → （7）16
（1101）2 → （13）10 → （d）16
所以0111 1101 → 0x7d

其实不需要转成十进制再转成十六进制，因为对照表已经展示了二进制和十六进制的对应关系。

将二进制数（10010）2转化成十六进制数

（10010）2 =（0001 0010）2 = (12) 16

二进制负整数 → 十六进制

1111 1101转成十六进制数

1111 转 f，1101 转 d，结果0xfd。

二进制小数 → 十六进制

将二进制数（0.1010）2转化为十六进制数

（0.10101）2=（0. 1010 1000）2=（0. A 8）16=（0.A8）16

二进制负小数 → 十六进制

直接根据对照表，4个二进制数对1个十六进制数，逐一替换即可。

十六进制 → 二进制

十六进制的正整数 → 二进制

将十六进制数（A7）16转换成二进制数

0xa7，默认是int类型，前面0省略，肯定是正数，转换的时候不必理会是否负数，直接转即可

（A7）16=（A 7）16=（1010 0111）2=（10100111）2，注意这里不是8位的补码，只是前面的0省略调了，这里可不是个负数，实际对应的十进制数是167。

0x7fd3 转成二进制数

7 转 0111
f 转1111
d 转 1101
3 转 0011

结果：01111111 11010011

十六进制的负整数 → 二进制

根据对照表直接转即可

十六进制的小数 → 二进制

将十六进制数（0.D4）16转换成二进制数

根据对照表直接转即可

（0.D4）16=（0. D 4）16=（0. 1101 0100）2=（0.110101）2

十六进制的负小数 → 二进制

根据对照表直接转即可

八进制和十六进制的转换

十六进制 → 八进制

先将十六进制转换成二进制，然后再转换成八进制

十六进制正整数 → 八进制

将十六进制数（A7）16转换成八进制数

（A7）16=（10100111）2=（010 100 111）2=（247）8

十六进制小数 → 八进制

将十六进制数（0.D4）16转换成八进制数

（0.D4）16=（0.1101 0100）2=（0. 110 101）2=（0.65）8

十六进制负整数 → 八进制

直接转成二进制，再转成八进制

十六进制负小数 → 八进制

直接转成二进制，再转成八进制

八进制 → 十六进制

八进制的正整数 → 十六进制

直接转成二进制，再转成十六进制

将八进制数（751）8转换成十六进制数

（751）8=（111 101 001）2=（0001 1110 1001）2=（1 E 9）16=（1E9）16

八进制的正小数 → 十六进制

将八进制数（0.16）8转换成十六进制数

（0.16）8=（0.001 110）2=（0. 0011 1000）2=（0.38）16

八进制的负整数 → 十六进制

根据「八进制与二进制对照表」转成二进制，再根据「十六进制与二进制对照表」转成十六进制

八进制的负小数 → 十六进制

根据「八进制与二进制对照表」转成二进制，再根据「十六进制与二进制对照表」转成十六进制

---

参考资料