P3701 -「伪模板」主席树【网络流,最大流】

正题

评测记录:https://www.luogu.org/recordnew/lists?uid=52918&pid=P3701

题目大意

给出若干个人的克制关系

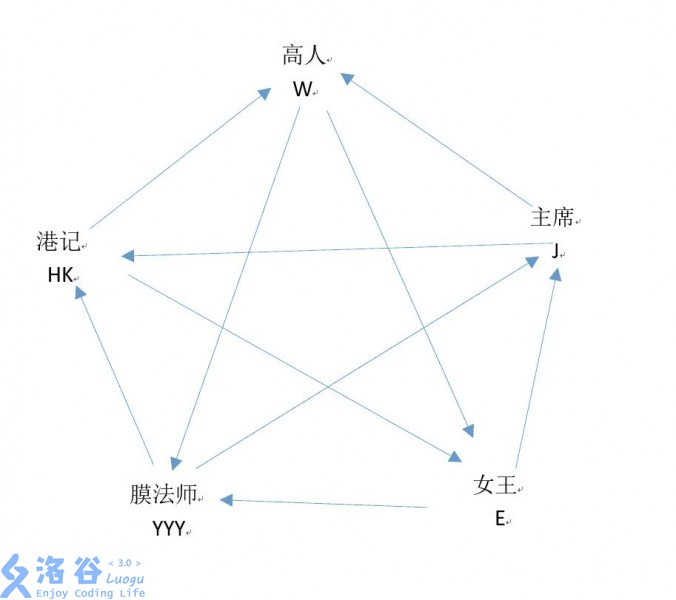
给出两边每个人的种类和血量。当两个人 $p k$ 后，双方各 $- 1 h p$ ，同一边的 $Y Y Y$ 可以给每个同一方的 $J+1hpJ\ +1hp$ ，血量为0时就不能 $p k$ 了，两个人之间不能重复 $p k$ 。每次选两个人出来比赛，比赛 $m$ 轮，求第一方最多能赢多少次。

解题思路

因为pk多次我们考虑网络流。
每次pk作为一个流量。
然后一个人能pk x(算上YYY给J的+1hp)次的话就用原点连这个点一条x的边。另一个边的就连汇点，然后可以击败就连一条1的边。
如样例

3 3
J W YYY
J HK E
2 2 2
2 2 2

图的情况
样例演示

$c o d e$

#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 2100
using namespace std;
struct line{int to,next,w;
}a[N*10];
struct player{char id[5];
}p[N],p2[N];
int n,m,x,y,d[N],tot=2,state[N],hp;
int head,tail,ls[N],s,e,ans,w,YYY1,YYY2;
void addl(int x,int y,int w)//建边
{a[tot].to=y;a[tot].next=ls[x];a[tot].w=w;ls[x]=tot++;a[tot].to=x;a[tot].next=ls[y];a[tot].w=0;ls[y]=tot++;
}
bool bfs()
{head=0;tail=1;memset(d,-1,sizeof(d));d[s]=0;state[1]=s;do{head++;int x=state[head];for (int q=ls[x];q;q=a[q].next){int y=a[q].to;if (a[q].w>0 && d[y]==-1){d[y]=d[x]+1;state[++tail]=y;if (y==e) return true;}}}while (head<tail);return false;
} 
int dinic(int x,int flow)
{int rest=0,k;if (x==e) return flow;for (int q=ls[x];q;q=a[q].next){int y=a[q].to;if (a[q].w>0 && d[y]==d[x]+1){rest+=(k=dinic(y,min(a[q].w,flow-rest)));a[q].w-=k;a[q^1].w+=k;}}if (!rest) d[x]=0;return rest;
}
int main()
{scanf("%d%d",&n,&m);e=n*2+2;s=n*2+1;for(int i=1;i<=n;i++) {scanf("%s",p[i].id);if(p[i].id[0]=='Y') YYY1++;}for(int i=1;i<=n;i++){scanf("%s",p2[i].id);if(p2[i].id[0]=='Y') YYY2++;}//以上为读入和记录YYY的个数for(int i=1;i<=n;i++){scanf("%d",&hp);if(p[i].id[0]=='J') addl(s,i,hp+YYY1);else addl(s,i,hp);}for(int i=1;i<=n;i++){scanf("%d",&hp);if(p2[i].id[0]=='J') addl(i+n,e,hp+YYY2);else addl(i+n,e,hp);}//以上为输入hp和主席特盘for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){char s1=p[i].id[0],s2=p2[j].id[0];if(s1=='E'&&(s2=='J'||s2=='Y')) addl(i,j+n,1);if(s1=='Y'&&(s2=='J'||s2=='H')) addl(i,j+n,1);if(s1=='H'&&(s2=='E'||s2=='W')) addl(i,j+n,1);if(s1=='W'&&(s2=='Y'||s2=='E')) addl(i,j+n,1);if(s1=='J'&&(s2=='H'||s2=='W')) addl(i,j+n,1);}}//击败连边while (bfs())ans+=dinic(s,1e9);if(ans>m) printf("%d",m);//对于m的特判else printf("%d",ans);
}