正题

比赛链接:https://ac.nowcoder.com/acm/contest/1080#question

---

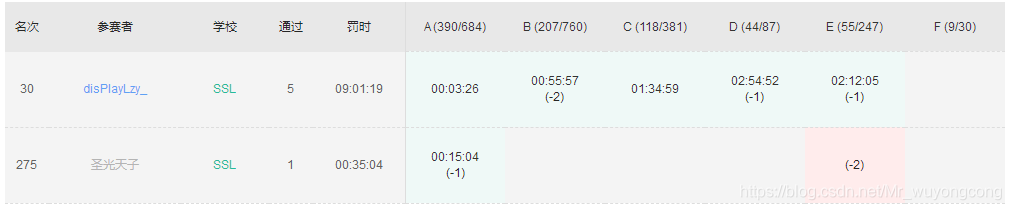
成绩

本届

升高二届

---

总结

以后还是不要写太多自己不擅长的写法，空间要多检查，不要像个傻逼一样啥都写错。

尽量不要为了省一点空间和时间写一些不舒服的东西，尽量在能通过的情况下自己怎么舒服怎么来就好了。

---

$T1:tokitsukazeandConnection$

题目大意

给出一个字符串，求里面的字母是不是都是连续的。

解题思路

暴力枚举，开个桶存储之前有没有出现过。

$code$

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n;
bool v[2333],flag;
char s[1000];
int main()
{scanf("%d%s",&n,s+1);for(int i=1;i<=n;i++){if(i==1||s[i]!=s[i-1]){if(v[s[i]]) {flag=1;break;}else v[s[i]]=1;}}if(flag) printf("NO");else printf("YES");
}

---

$T2:tokitsukazeandHashTable$

题目大意

将$n$个数字插入长度为$n$的哈希表，数值为$x\%n$，求最后$hash$表的状态。

解题思路

考虑到暴力枚举肯定会被卡成$O(n^2)$，所以我们用树状数组+二分可以做到$O({\log }^{2}n)$找到下一个空位，若没有空位我们就直接用最前方的空位即可。

$code$

#include<cstdio>
#define lowbit(x) x&-x
using namespace std;
const int N=1100000;
int n,op,v[N],t[N];
void add(int x,int val)
{while(x<=n){t[x]+=val;x+=lowbit(x);}
}
int ask(int x)
{int ans=0;while(x){ans+=t[x];x-=lowbit(x);}return ans;
}
int main()
{scanf("%d",&n);op=1;for(int i=1;i<=n;i++){int X,x;scanf("%d",&X);x=X%n+1;int l=x,r=n,w=ask(x-1);while(l<=r){int mid=(l+r)/2;if(ask(mid)-w==mid-(x-1)) l=mid+1;else r=mid-1;}if(l<=n&&!v[l])v[l]=X+1,add(l,1);else{while(v[op])op++;v[op]=X+1;add(op,1);}}for(int i=1;i<=n;i++)printf("%d ",v[i]-1);
}

---

$T3:tokitsukazeandSoldier$

题目大意

若干个人，第$i$个战力为$v_i$，若这个人在团里要求不超过$s_i$个人，选择若干个人能组成的最大战斗力。

解题思路

这个十分显然的贪心题目，我们先按照$s_i$从大到小排序，然后我们可以开始枚举，我们发现我们枚举到$i$时人数不能超过$s_i$个。我们可以维护一个优先队列，每次$s_i$缩小时我们就将价值最小的给弹出来就好了。

$code$

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#define ll long long
using namespace std;
const ll N=110000;
priority_queue<ll> q;
struct node{ll v,s;
}a[N];
ll n,ans,maxs;
bool cMp(node x,node y)
{return x.s>y.s;}
int main()
{scanf("%lld",&n);for(ll i=1;i<=n;i++)scanf("%lld%lld",&a[i].v,&a[i].s);sort(a+1,a+1+n,cMp);for(ll i=1;i<=n;i++){while(q.size()>=a[i].s)ans+=q.top(),q.pop();q.push(-a[i].v);ans+=a[i].v;maxs=max(maxs,ans);}printf("%lld",maxs);
}

---

$T4:tokitsukazeandEvent$

题目大意

一张无向图，普通模式下边权为$a_i$，夜战模式边权为$b_i$。在难度$k$时可以在$k\sim n$中任意一个点转换为夜战模式，但不能转回来。
求难度在$1\sim n$的情况下分别的最短路。

解题思路

我们设$dis{1}_i$表示普通模式下$s\sim i$的最短路长度，$dis{2}_i$表示夜战模式下$i\sim t$的最短路。

对于难度为$k$答案显然为min{dis1i+dis2i}(i≥k)min\{dis1_i+dis2_{i}\}(i\geq k)min{dis1i​+dis2i​}(i≥k)。我们倒着枚举即可。

$code$

#include<cstdio>
#include<cstring>
#include<queue>
#define ll long long
using namespace std;
const ll N=100010,M=200010;
struct node{ll pos,dis;bool operator<(const node &x)const{return x.dis<dis;}
};
struct edge_node{ll to,next,a,b;
}a[M];
priority_queue<node> q;
ll tot,ls[N],dis[N],dis2[N],n,m,s,t,f[N],ans;
bool v[N];
void addl(ll x,ll y,ll A,ll b)
{a[++tot].to=y;a[tot].next=ls[x];ls[x]=tot;a[tot].a=A;a[tot].b=b;
}
void dij(ll s)
{dis[s]=0;q.push((node){s,0});while(!q.empty()){node tmp=q.top();q.pop();ll x=tmp.pos;if(v[x]) continue;v[x]=1;for(ll i=ls[x];i;i=a[i].next){ll y=a[i].to;if(dis[y]>dis[x]+a[i].a){dis[y]=dis[x]+a[i].a;if(!v[y])q.push(node{y,dis[y]});}}}
}
void dij2(ll s)
{dis2[s]=0;memset(v,0,sizeof(v));q.push((node){s,0});while(!q.empty()){node tmp=q.top();q.pop();ll x=tmp.pos;if(v[x]) continue;v[x]=1;for(ll i=ls[x];i;i=a[i].next){ll y=a[i].to;if(dis2[y]>dis2[x]+a[i].b){dis2[y]=dis2[x]+a[i].b;if(!v[y])q.push(node{y,dis2[y]});}}}
}
int main()
{scanf("%lld%lld",&n,&m);memset(dis2,127,sizeof(dis2));memset(dis,127,sizeof(dis));for(ll i=1;i<=m;i++){ll x,y,A,b;scanf("%lld%lld%lld%lld",&x,&y,&A,&b);addl(x,y,A,b);addl(y,x,A,b);}scanf("%lld%lld",&s,&t);dij(s);dij2(t);ans=1e18;for(ll i=n;i>=1;i--)ans=min(ans,dis[i]+dis2[i]),f[i]=ans;for(ll i=1;i<=n;i++)printf("%lld\n",f[i]);
}

---

$T5:tokitsukazeandSegmentation$

题目大意

给出一串数字，求将数字划分要求

1. 没有前导0
2. 每个部分都能被$3$整除

求划分方案数。

解题思路

很显然的数位$dp$
设$f_{i,j,0/1}$表示到第$i$为，当前划分的数字之和为$j$，是不是纯0构成的。

$code$

#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;
const ll N=110000,XJQ=998244353;
ll n,f[N][3][2];
char s[N];
int main()
{scanf("%lld%s",&n,s+1);for(int i=1;i<=n;i++)s[i]-='0';f[1][s[1]%3][s[1]!=0]=1;for(ll i=1;i<=n;i++){(f[i][s[i]%3][s[i]!=0]+=f[i-1][0][0]+f[i-1][0][1])%=XJQ;for(ll j=0;j<3;j++)(f[i+1][(j+s[i+1])%3][1]+=f[i][j][1])%=XJQ;}printf("%lld",(f[n][0][0]+f[n][0][1])%XJQ);
}