极限
百度百科
1.数列极限
百度百科
1.1 数列
1.2 数列极限
1.3 单调收敛原理
{xn}\{x_n\}{xn}单调递增且{xn}\{x_n\}{xn}有上界(可以找到实数M使{xn}\{x_n\}{xn}中任意一项小于M),{xn}\{x_n\}{xn}收敛(存在象限a)(单调递减同理)
2.函数极限
百度百科
2.1 定义
(a的去心邻域:(a−δ,a)∪(a,a+δ)(a-\delta,a) \cup (a,a + \delta)(a−δ,a)∪(a,a+δ))
(a的左邻域:(a−δ,a)(a-\delta,a)(a−δ,a))
(a的右邻域:(a,a+δ)(a,a + \delta)(a,a+δ))
2.2 函数的单侧极限
设函数f(x)f(x)f(x)在点x0x_0x0的左邻域内有定义,如果存在常数A,对于任意给定的正数ϵ\epsilonϵ,总存在正数δ\deltaδ,使得当xxx从左侧趋于x0x_0x0时,也即xxx满足的不等式为0<x0−x<δ0<x_0-x<\delta0<x0−x<δ时,函数值f(x)f(x)f(x)都满足不等式
∣f(x)−A∣<ϵ|f(x)-A|<\epsilon∣f(x)−A∣<ϵ,
则常数A就叫做函数f(x)f(x)f(x)在x0x_0x0处的左极限,记作
limx→x0−f(x)=A\lim\limits_{x\to x_0^-}f(x)=Ax→x0−limf(x)=A
同样地,设函数f(x)f(x)f(x)在点x0x_0x0的右邻域内有定义,如果存在常数A,对于任意给定的正数ϵ\epsilonϵ,总存在正数δ\deltaδ,使得当xxx从右侧趋于x0x_0x0时,也即xxx满足的不等式为0<x−x0<δ0<x-x_0<\delta0<x−x0<δ时,函数值f(x)f(x)f(x)都满足不等式
∣f(x)−A∣<ϵ|f(x)-A|<\epsilon∣f(x)−A∣<ϵ,
则常数A就叫做函数f(x)f(x)f(x)在x0x_0x0处的右极限,记作
limx→x0+f(x)=A\lim\limits_{x\to x_0^+}f(x)=Ax→x0+limf(x)=A
2.3 函数在无穷远处的极限
设函数f(x)f(x)f(x)在(t,+∞)(t,+\infty)(t,+∞)内有定义,如果存在常数A,对于任意给定的正数ϵ\epsilonϵ,总存在正数MMM,使得当xxx满足不等式x>Mx>Mx>M时,函数值f(x)f(x)f(x)都满足不等式
∣f(x)−A∣<ϵ|f(x)-A|<\epsilon∣f(x)−A∣<ϵ,
则常数A就叫做函数f(x)f(x)f(x)在x→+∞x\to+\inftyx→+∞时的极限,记作
limx→+∞f(x)=A\lim\limits_{x\to +\infty}f(x)=Ax→+∞limf(x)=A
类似的,可以定义函数在负无穷远处的极限
2.4 两个基本极限
limx→0sinxx=1\lim\limits_{x\to0}\frac{sin\space x}{x}=1x→0limxsin x=1
limn→+∞(1+1n)n=e\lim\limits_{n\to+\infty}(1+\frac{1}{n})^n=en→+∞lim(1+n1)n=e
2.5 运算法则
2.6 连续函数
导数
百度百科
1.定义
2.几何意义
3.导函数
4.常见导数公式
(C)′=0(C为常数)(C)^\prime=0(C为常数)(C)′=0(C为常数)
(xa)′=axa−1(a为任意实数)(x^a)^\prime=ax^{a-1}(a为任意实数)(xa)′=axa−1(a为任意实数)
(sinx)′=cosx,(cosx)′=−sinx(sin\space x)^\prime=cos\space x,(cos\space x)^\prime=-sin\space x(sin x)′=cos x,(cos x)′=−sin x
(ax)′=axlna,(ex)′=ex(a^x)^\prime=a^xln\space a,(e^x)^\prime=e^x(ax)′=axln a,(ex)′=ex
(logax)′=1xlna,(lnx)′=1x(log_ax)^\prime=\frac{1}{x\space ln\space a},(ln\space x)^\prime=\frac{1}{x}(logax)′=x ln a1,(ln x)′=x1
(tanx)′=1cos2x,(cotx)′=−1sin2x,(ln∣x∣)′=1x(tan\space x)^\prime=\frac{1}{cos^2x},(cot\space x)^\prime=-\frac{1}{sin^2x},(ln|x|)^\prime=\frac{1}{x}(tan x)′=cos2x1,(cot x)′=−sin2x1,(ln∣x∣)′=x1
(arcsinx)′=11−x2,(arccosx)′=−11−x2,(arctanx)′=11+x2(arcsin\space x)^\prime=\frac{1}{\sqrt{1-x^2}},(arccos\space x)^\prime=-\frac{1}{\sqrt{1-x^2}},(arctan\space x)^\prime=\frac{1}{1+x^2}(arcsin x)′=1−x21,(arccos x)′=−1−x21,(arctan x)′=1+x21
5.求导法则
5.1 导数的四则运算法则
-
[(f(x)±g(x)]′=f′(x)±g′(x)[(f(x)\pm g(x)]^\prime=f^\prime(x)\pm g^\prime(x)[(f(x)±g(x)]′=f′(x)±g′(x)
-
[f(x)⋅g(x)]′=f′(x)g(x)+f(x)g′(x)[f(x)\cdot g(x)]^\prime=f^\prime(x)g(x)+f(x)g^\prime(x)[f(x)⋅g(x)]′=f′(x)g(x)+f(x)g′(x)
推论:
若函数f1(x),f2(x),...,fn(x)f_1(x),f_2(x),...,f_n(x)f1(x),f2(x),...,fn(x)都可导,其中n≥2,n∈Nn\geq2,n\in Nn≥2,n∈N,那么(f1f2...fn)′=f1′f2...fn−1fn+f1f2′...fn−1fn+...+f1f2...fn−1fn′(f_1f_2...f_n)^\prime=f_1^\prime f_2...f_{n-1}f_n+f_1f_2^\prime...f_{n-1}f_n+...+f_1f_2...f_{n-1}f_n^\prime(f1f2...fn)′=f1′f2...fn−1fn+f1f2′...fn−1fn+...+f1f2...fn−1fn′ -
[f(x)g(x)]′=f′(x)g(x)−f(x)g′(x)g2(x)[\frac{f(x)}{g(x)}]^\prime=\frac{f^\prime(x)g(x)-f(x)g^\prime(x)}{g^2(x)}[g(x)f(x)]′=g2(x)f′(x)g(x)−f(x)g′(x)
推论:
若函数f(x)f(x)f(x)可导,且f(x)≠0f(x)\ne0f(x)=0,则[1f(x)]′=−f′(x)f2(x)[\frac{1}{f(x)}]^\prime=-\frac{f^\prime(x)}{f^2(x)}[f(x)1]′=−f2(x)f′(x)
5.2 复合函数求导法则
若函数u=g(x)u=g(x)u=g(x)与函数y=f(u)y=f(u)y=f(u)均可导,则复合函数y=f[g(x)]y=f[g(x)]y=f[g(x)]可导,且[f(g(x))]′=f′(g(x))⋅g′(x)[f(g(x))]^\prime=f^\prime(g(x))\cdot g^\prime(x)[f(g(x))]′=f′(g(x))⋅g′(x),或记成dydx=dydu⋅dudx\frac{dy}{dx}=\frac{dy}{du}\cdot \frac{du}{dx}dxdy=dudy⋅dxdu
定积分
百度百科
1.定积分的几何意义
1.1 黎曼和
1.2 曲边梯形的面积
设λ=max{△x1,△x2,…,△xn}λ=max\{△x_1, △x_2, …, △x_n\}λ=max{△x1,△x2,…,△xn},如果当λ→0λ\to 0λ→0时,黎曼和的极限存在,那么就定义这个极限为曲边梯形的面积
1.3 定积分定义
2.定积分的计算
2.1 牛顿-莱布尼茨公式(微积分基本定理)
设f∈C[a,b]f\in C[a,b]f∈C[a,b],如果F(x)F(x)F(x)是f(x)f(x)f(x)在区间[a,b][a,b][a,b]上的一个原函数,即F′(x)=f(x)F^\prime(x)=f(x)F′(x)=f(x),那么










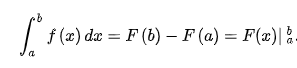


![YbtOJ#20236-[冲刺NOIP2020模拟赛Day9]红点蓝点【线段树,堆】](http://pic.xiahunao.cn/YbtOJ#20236-[冲刺NOIP2020模拟赛Day9]红点蓝点【线段树,堆】)

)
)
![[XSY] 分割(dfs树)](http://pic.xiahunao.cn/[XSY] 分割(dfs树))
![P4068-[SDOI2016]数字配对【二分,费用流】](http://pic.xiahunao.cn/P4068-[SDOI2016]数字配对【二分,费用流】)

)

![[XSY] 相似(DP套DP)](http://pic.xiahunao.cn/[XSY] 相似(DP套DP))
![P3295-[SCOI2016]萌萌哒【ST表,并查集】](http://pic.xiahunao.cn/P3295-[SCOI2016]萌萌哒【ST表,并查集】)

)
)
![[XSY] 线图(树形DP、分类讨论)](http://pic.xiahunao.cn/[XSY] 线图(树形DP、分类讨论))



![YbtOJ#20239-[冲刺NOIP2020模拟赛Day10]连边方案【状压dp】](http://pic.xiahunao.cn/YbtOJ#20239-[冲刺NOIP2020模拟赛Day10]连边方案【状压dp】)