正题

luogu 7472

---

题目大意

给出一个正方形点阵，让你选择两个点，分别向两个方向移动（必须是45度），每到一个点就得到该点的贡献（不重复得），遇到墙壁反射，问你最大贡献

---

解题思路

不难发现，从每一个点向任意方向移动总会遇到左边的边界，且每个边界最多走一遍（有贡献的），走的路径如下

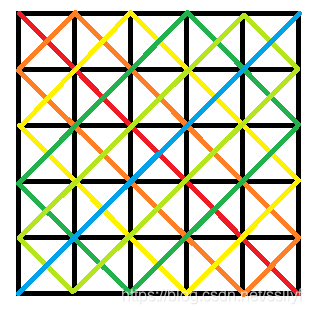
那么可以枚举左边的边界，然后向左下角运动

先处理出每种方案的贡献，以及和边界的交点

然后枚举所选的两条线，再通过和边界的交点得出两条线的交点，减去即可

---

代码

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
#define N 1010
using namespace std;
int n, x, y, xx, yy, ans, s[N], u[N], r[N], d[N], a[N][N];
int js(int x, int y)
{int g = 1;if (x == n) g <<= 1;//对角线if (y == 1) g <<= 1;return (a[x + y >> 1][1 + (x - y >> 1)] + a[1 + (u[x] - u[y] >> 1)][u[x] + u[y] >> 1] + a[r[y] + r[x] >> 1][n - (r[y] - r[x] >> 1)] + a[n - (d[y] - d[x] >> 1)][d[y] + d[x] >> 1]) / g;//减去交点
}
int main()
{scanf("%d", &n);for (int i = 1; i <= n; ++i)for (int j = 1; j <= n; ++j)scanf("%d", &a[i][j]);for (int i = 1; i <= n; ++i){x = i;y = 1;xx = 1;yy = 1;if (i == 1) u[i] = 1;if (i == n){d[i] = 1;xx = -1;}s[i] = a[x][y];x += xx;y += yy;while(x != i || y != 1){if (x == n) xx = -1, d[i] = y;//找和边界的交点if (x == 1) xx = 1, u[i] = y;if (y == n) yy = -1, r[i] = x;s[i] += a[x][y];if ((x == 1 || x == n) && (y == 1 || y == n)) break;x += xx;y += yy;}for (int j = 1; j < i; ++j){if ((i + j) & 1) ans = max(ans, s[i] + s[j]);//如果距离为奇数那么不相交在整点上else ans = max(ans, s[i] + s[j] - js(i, j));}}printf("%d", ans);return 0;
}