数位dp

例题：

NC116652 uva11038 How many 0’s

题目：输入a和b，求a到b的所有数之中有多少0出现
题解：
先算个位，个位是0的情况有x种
再算十位，十位是0的情况有y种
…
一共是x+y+…

用数位dp做
dp[i]中存的是从0~99…9(共i个9)中0的个数（不含前导0）
dp0[i]中存放的是00…0~99…9(共i个0，i个9)中0的个数（含前导0）
dp0[i]=dp0[i-1] * 10+power * (10,i-1)
dp[i]=dp[i-1]+dp0[i-1]*9

NC15035 送分了QAQ

每次给出一个区间[n,m],求包含38或者4的数字的个数
题解：
dp[i][st]从高到低数第i为对应的情况为st的数字个数，
st=0表示没有4也没有38
st=1表示有38或者4但当前位是3
dt=2表示有4或者38
dp[i][0]=9*dp[i-1][0]-dp[i-1][1]
dp[i][1]=dp[i-1][0]
dp[i][2]=dp[i-1][2]*10+dp[i-1][1]+dp[i-1][0]
边界：dp[0][0]=1

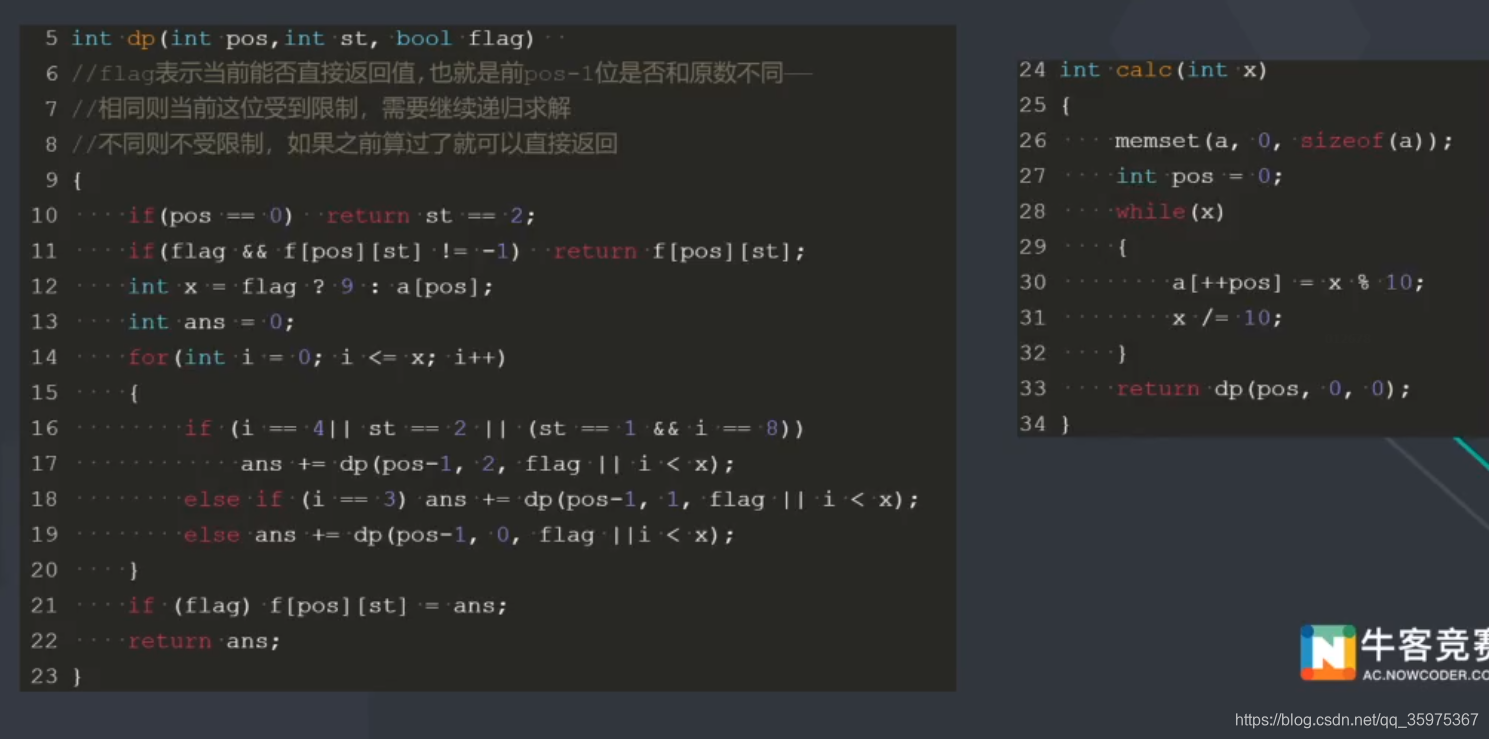
NC20669 诡异数字

题目：
一个区间[l,r]和多个约束，约束为数字x在数字串中连续出现的次数不能大于len，求出这个区间内满足这些约束的数字个数（不含前导0）x为0~9
题解：
dp[i][x][cnt]表示从高往低第i位的数字是x，且x已经连续出现了cnt次的合法数字个数

代码：
模板

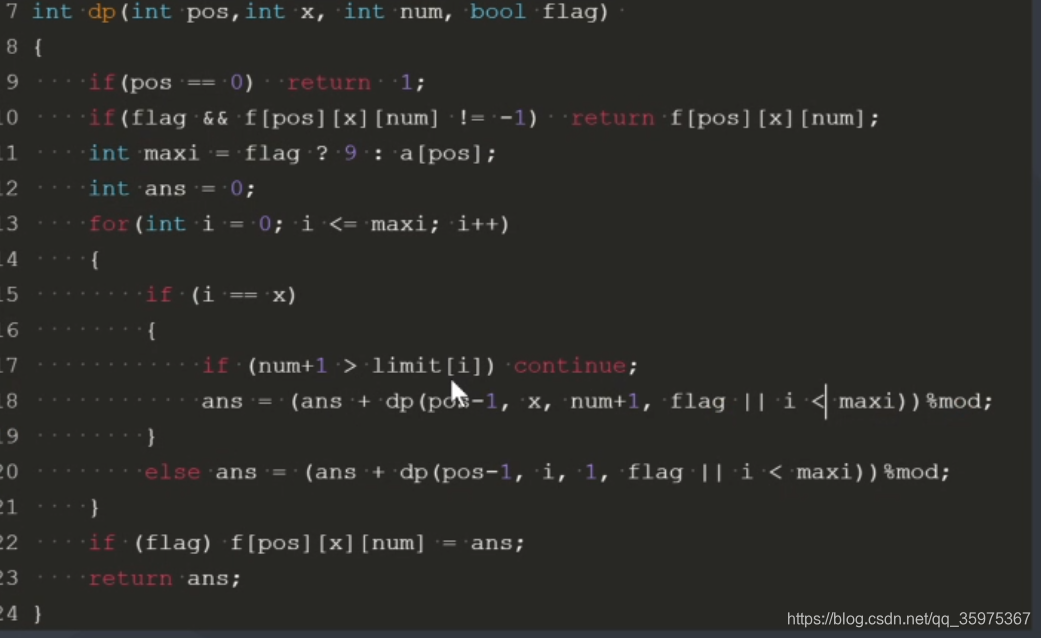
int dp(int pos,int x,int num,bool flag)
{//num当前这位是什么 if(pos==0)return 1;//if(flag&&f[pos][x][num]!=-1)return f[pos][x][num];//已经算好的直接返回 int maxi=flag?9:a[pos];//当然能枚举的最多数 int ans=0;for(int i=0;i<maxi;i++){if(i==x)//如果相等 {if(num+1>limit[i])continue;//判断是否数字非法 ans=(ans+dp(pos-1,x,num+1,flag||i<maxi))%mod;//如果合法，加上继续向后dp }else ans=(ans+dp(pos-1,i,1,flag||i<maxi))%mod;//如果不相等，新的数（即不连续） } if(flag)f[pos][x][num]=ans;//更新f return ans;} 

NC20665 7的意志

题目：
定义一个序列：7,77,777,7777…7777777…
如果一个整数能被序列a中的任意一个数字整除，并且其数位之和为序列a中任意一个数字的倍数，那么这个数字就含有7的意志，给定范围[n,m]问有多少数有7的意志
1<n<m<1e18
题解：
%7,%77…=0，所以只用%7即可
dp[pos][pre][sum] 前pos位的数的和%7的余数为pre，数位和%7为sum的个数

 for(i=0-->maxi)ans+=dp(i-1.(pre*10+i)%7,(sum+i%7),flag) 

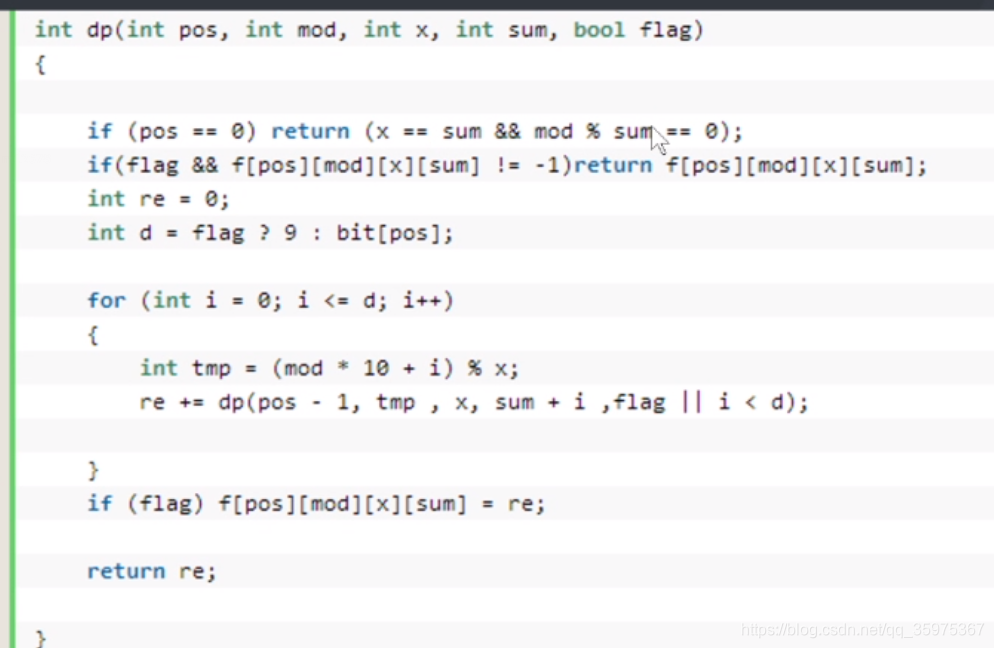
NC17385 Beautiful Numbers

F(x)为x各个位数的和
求x%F(x）==0的数的个数（最多12位）
题解：
dp[pos][x][mod][sum]表示前pos位数除以x的余数为mod，且前pos位的和为sum的数字个数
x从0~12*9枚举

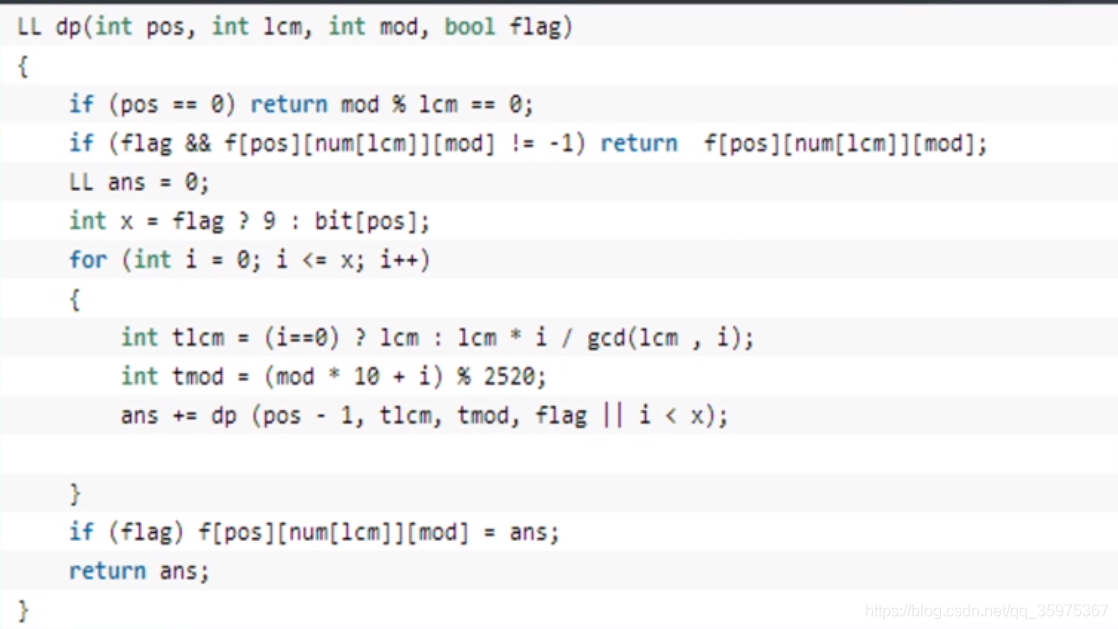
CF55D NC108918 Beautiful numbers

区间[l,r]中有多少数能够整除他自身各位数，也就等价于在区间[l，r]中有多少数能够整除他自身各位数的最小公倍数

习题：

题目地址

NC17867 明七暗七

NC19327 好朋友

NC19945 [CQOI2016]手机号码

NC20268 [SCOI2009]WINDY数

NC20287 [SCOI2012]BLINKER的仰慕者

NC20293 [SCOI2013]数数

NC20298 [SCOI2014]方伯伯的商场之旅

NC20491 [ZJOI2010]COUNT 数字计数

NC210885 计数问题