[ZJOI2007]棋盘制作

题意：

选取最大的01相邻的正方形和矩形，输出面积

题解：

单调栈

如图：
左图为题目给的样例，我们要找01相邻最大的正方形

就是图中绿色部分
矩形就是如图
01相邻不好找，我们可以转换下思路，仔细看看正方形和矩形的两个图，0和1相邻说明0和1同行但列差1，同列但行差1，所以我们可以通过坐标奇偶性取反
奇数行偶数列取反，偶数行奇数列取反
这样就会得到：
第一个图的右图：

这样我们就将01问题转换成求最大的全1正方形和矩阵问题
最大正方形的边长其实就是最大矩阵的最小边

代码：

#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <ctime>
#include <vector>
#include <queue>
#include <map>
#include <set>
using namespace std;
typedef long long LL;
const int inf = (1<<30);
const int MAXN = 2011;
int n,m,ans,ans2;
int a[MAXN][MAXN];
int ri[MAXN][MAXN];//可以往右延伸多少
int st[MAXN],top,up[MAXN];inline int getint()
{int w=0,q=0; char c=getchar();while((c<'0' || c>'9') && c!='-') c=getchar(); if(c=='-') q=1,c=getchar();while (c>='0' && c<='9') w=w*10+c-'0', c=getchar(); return q ? -w : w;
}
inline void getR(){  for(int i=1;i<=n;i++){for(int j=1;j<=m;j++) if(a[i][j]) ri[i][j]=ri[i-1][j]+1; else ri[i][j]=0; ri[i][m+1]=-1;}
}
inline void getA(){for(int i=1;i<=n;i++){top=0;//每一行清空栈 for(int j=1;j<=m+1;j++){if(top==0||ri[i][j]>=ri[i][st[top]]){st[++top]=j;}else {	int id; while(top!=0&&ri[i][j]<ri[i][st[top]]){id=st[top];top--;int w=min(j-id,ri[i][id]);ans=max(ans,w*w);ans2=max(ans2,(j-id)*ri[i][id]);}st[++top]=id;//将最后一次出栈的栈顶元素延申并入栈ri[i][id]=ri[i][j]; }}}}
void printA(){for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cout<<a[i][j]<<" "; }cout<<endl;}cout<<endl;
}
inline void work(){n=getint(); m=getint();for(int i=1;i<=n;i++) for(int j=1;j<=m;j++)a[i][j]=getint();for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)if(((i&1)==(j&1) && a[i][j])||((i&1)!=(j&1) && !a[i][j])) a[i][j]=1;else a[i][j]=0;//printA();getR();getA(); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) a[i][j]=!a[i][j];//printA();getR(); getA(); printf("%d\n%d",ans,ans2);
}int main()
{//freopen("P1169_1.in","r",stdin);work();return 0;
}

悬线法

学会再更新

---

9.9 刚学会，重新更新
悬线法理解

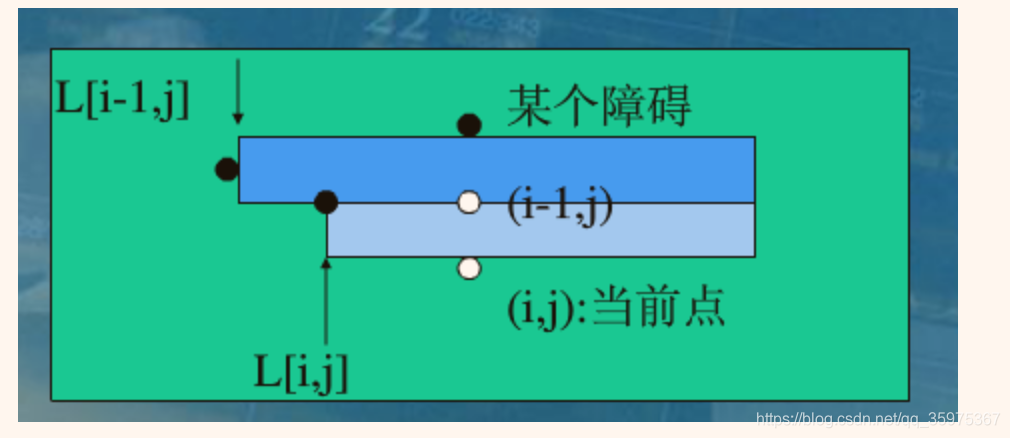
矩形其实是由一个线左右移动而形成，而我们要做的就是枚举这样的线，并通过题目限制来左右滑动生成矩阵，并保留最大矩阵即可
复杂度O ( n ∗ m )

#include<cstdio>
#define N 2005
#define max(a,b) a>b?a:b
#define min(a,b) a<b?a:b
using namespace std;
int up[N][N],left[N][N],right[N][N],ansa,ansb,a[N][N],m,n;
int main(){scanf("%d%d",&n,&m);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){up[i][j]=1;left[i][j]=j;right[i][j]=j;scanf("%d",&a[i][j]);// up 初值，读入，left/right 最初值}for(int i=1;i<=n;i++)for(int j=2;j<=m;j++)if(a[i][j]^a[i][j-1])//如果点i j与点i j-1不相等，即一个为0一个为1 left[i][j]=left[i][j-1];//左边界可以共享 for(int i=1;i<=n;i++)for(int j=m;j>1;j--)if(a[i][j]^a[i][j-1])right[i][j-1]=right[i][j];//left/right初值，即（i，j）点向左/右的最大宽度//之上均为左右不同            for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){if(i>1&&a[i][j]^a[i-1][j])//上下点不同 {up[i][j]=up[i-1][j]+1;//更新高度 left[i][j]=max(left[i][j],left[i-1][j]);right[i][j]=min(right[i][j],right[i-1][j]);} int a=right[i][j]-left[i][j]+1;int b=min(a,up[i][j]);ansa=max(ansa,b*b);//求正方形 ansb=max(ansb,a*up[i][j]);//求长方形 }printf("%d\n%d",ansa,ansb);
}