正题

题目链接:https://www.ybtoj.com.cn/contest/116/problem/3

---

题目大意

给出两个大小分别为$n,m$的点集$A,B$。

求出$B$的一个最小子集使得该子集的凸包包含了所有点集$A$中的点。

无解输出$-1$

$2\le n\le 10^5,3\le m\le 500$

---

解题思路

选出的子集肯定是一个凸包，凸包就是相邻点连边之间的半平面交。

所以可以理解为我们要找到一些点对使得它们的半平面包含点集$A$。

如果$x->y$的半平面（左右都一样，反过来就是了）包含点集$A$，那么$x$向$y$连边，那么问题就变为了求图的最小环。这个可以$Floyd$解决。

如何判断一个半平面是否包含点集$A$？

一个类似旋转卡壳的想法是对于给出的这个半平面的斜率，我们在点集$A$的凸包上找到两个节点卡住它。（如下图）

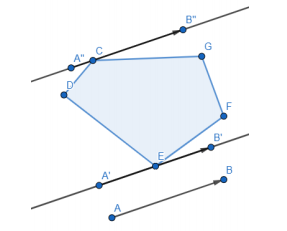
然后判断这两个点是否在半平面内就好了。

挺麻烦的，再简化一下，我们将$A$的凸包用$x$坐标最大/小的两个节点分成两半，那么凸包就变成了一个上凸壳和一个下凸壳。

然后我们要找到的两个点，这个两个点肯定是一个在上一个在下的，我们根据半平面的斜率在上下凸壳上面二分一下就好了。

时间复杂度$O(n+m^2\log n+m^3)$

---

code

#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;
const ll N=1e5+10,M=510;
struct point{ll x,y;point(ll xx=0,ll yy=0){x=xx;y=yy;return;}
}g[N],u[N],v[N],s[N],p[M];
ll n,m,uc,vc,f[M][M],h[M][M],ans;
point operator+(point a,point b)
{return point(a.x+b.x,a.y+b.y);}
point operator-(point a,point b)
{return point(a.x-b.x,a.y-b.y);}
ll operator*(point a,point b)
{return a.x*b.y-a.y*b.x;}
ll solve(point *a,ll n,ll op){ll top;s[top=1]=a[1];for(ll i=2;i<=n;i++){while(top>1&&(s[top]-s[top-1])*(a[i]-s[top-1])*op>=0)top--;s[++top]=a[i];}for(ll i=1;i<=top;i++)a[i]=s[i];return top;
}
bool check(point a,point b){ll op=1;if(a.x>b.x)swap(a,b),op=-1;ll l=1,r=uc-1;while(l<=r){ll x=(l+r)>>1;if((b-a)*(u[x+1]-u[x])>=0)l=x+1;else r=x-1; }if((b-a)*(u[l]-a)*op<0)return 0;l=1,r=vc-1;while(l<=r){ll x=(l+r)>>1;if((b-a)*(v[x+1]-v[x])<=0)l=x+1;else r=x-1;}if((b-a)*(v[l]-a)*op<0)return 0;return 1;
}
bool cmp(point a,point b)
{return a.x<b.x;}
signed main()
{freopen("lo.in","r",stdin);freopen("lo.out","w",stdout);scanf("%lld%lld",&n,&m);ll L=1,R=1;for(ll i=1;i<=n;i++)scanf("%lld%lld",&g[i].x,&g[i].y);sort(g+1,g+1+n,cmp);for(ll i=1;i<=n;i++){ll w=(g[n]-g[1])*(g[i]-g[1]);if(w>=0)u[++uc]=g[i];if(w<=0)v[++vc]=g[i];}uc=solve(u,uc,1);vc=solve(v,vc,-1);for(ll i=1;i<=m;i++)scanf("%lld%lld",&p[i].x,&p[i].y);for(ll i=1;i<=m;i++)for(ll j=1;j<=m;j++){if(i==j){h[i][j]=f[i][j]=1e9;continue;}h[j][i]=f[i][j]=check(p[i],p[j])?1:1e9;}for(ll k=1;k<=m;k++)for(ll i=1;i<=m;i++)for(ll j=1;j<=m;j++)f[i][j]=min(f[i][j],f[i][k]+f[k][j]);ans=1e9;for(ll i=1;i<=m;i++)for(ll j=1;j<=m;j++)ans=min(ans,f[i][j]+h[i][j]);if(ans>=1e9)puts("-1");else printf("%lld\n",ans);return 0;
}