题目大意

平面上有n个点，给出m个询问，每个询问要回答从x轮流往右往左去到最远的点，最后到达的点

---

解题思路

对于每个询问，每次二分左右可以到多远，直到不能动为止

考虑时间，对于重复走一个范围的，可以直接模掉

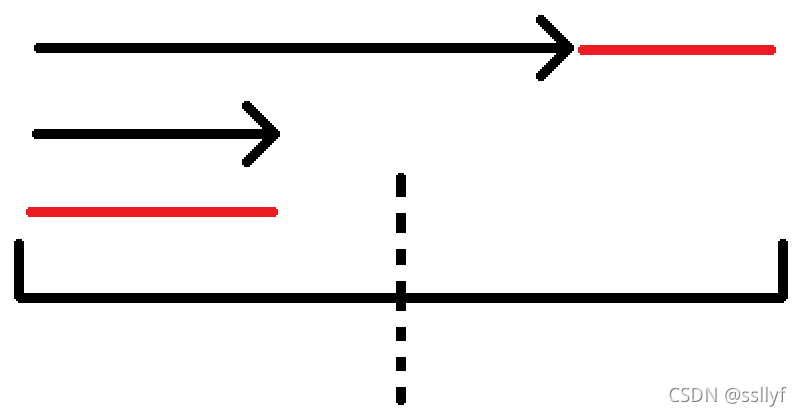
对于范围缩小的（如下图），如果走了黑的的一段，则下一段的长度不会大于红色的一段（上面是因为如果大于则可以走完一程，下面的是因为范围最大为红色），所以每一次走的距离会小于上一次的一半

所以时间复杂度为$O(mlognlog10^9)$

code

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
#define N 200021
#define mp make_pair
#define fs first
#define sn second
using namespace std;
ll n,m,x,k,l,r,L,R,mid,len,v[N],a[N];
pair<ll,ll>b[N];
int main()
{scanf("%lld%lld",&n,&m);for(ll i=1;i<=n;++i){scanf("%lld",&x);b[i]=mp(x,i);}sort(b+1,b+1+n);for(ll i=1;i<=n;++i)v[b[i].sn]=i,a[i]=b[i].fs;len=(a[n]-a[1])*2;if(n==1){while(m--)puts("1");return 0;}while(m--){scanf("%lld%lld",&x,&k);x=v[x];k%=len;l=x;r=n;while(l<r){//先走到最后面mid=l+r+1>>1;if(k<a[mid]-a[x])r=mid-1;else l=mid;}L=1;R=l;k-=a[l]-a[x];while(L<R){k%=(a[R]-a[L])*2;l=L;r=R;while(l<r){//来回走mid=l+r>>1;if(k<a[R]-a[mid])l=mid+1;else r=mid;}L=l;k-=a[R]-a[l];l=L;r=R;while(l<r){mid=l+r+1>>1;if(k<a[mid]-a[L])r=mid-1;else l=mid;}R=l;k-=a[l]-a[L];}printf("%lld\n",b[L].sn);}return 0;
}