前言：

在一个数列a中，对于一个大区间A和组成它的两个小区间a，b；
可以借其中两个区间的信息推导出第三个区间的信息
不妨称这样的问题叫做数列的信息传递问题
（具体来说就是：给出[l1,r1]的信息与[r1,r2]的信息（这里也可能是[r1+1,r2]，只是在连点的细节上略有不同），那么就可以求出[l1,r2]的信息）

看一个例子：

若分别已知区间[1,4][5,7][8,10][11,15]的总和的奇偶性
那么显然可以推出[1,15]的总和的奇偶性

从上面可以看出：这种信息推导具有传递性
那么对于这样的问题，我们可以将其转化为点的合并问题
本文所举的具有这样性质的信息有两个，一个是加和奇偶性，一个是取模
那么我们开始吧：

一、数列询问（取模）

解析

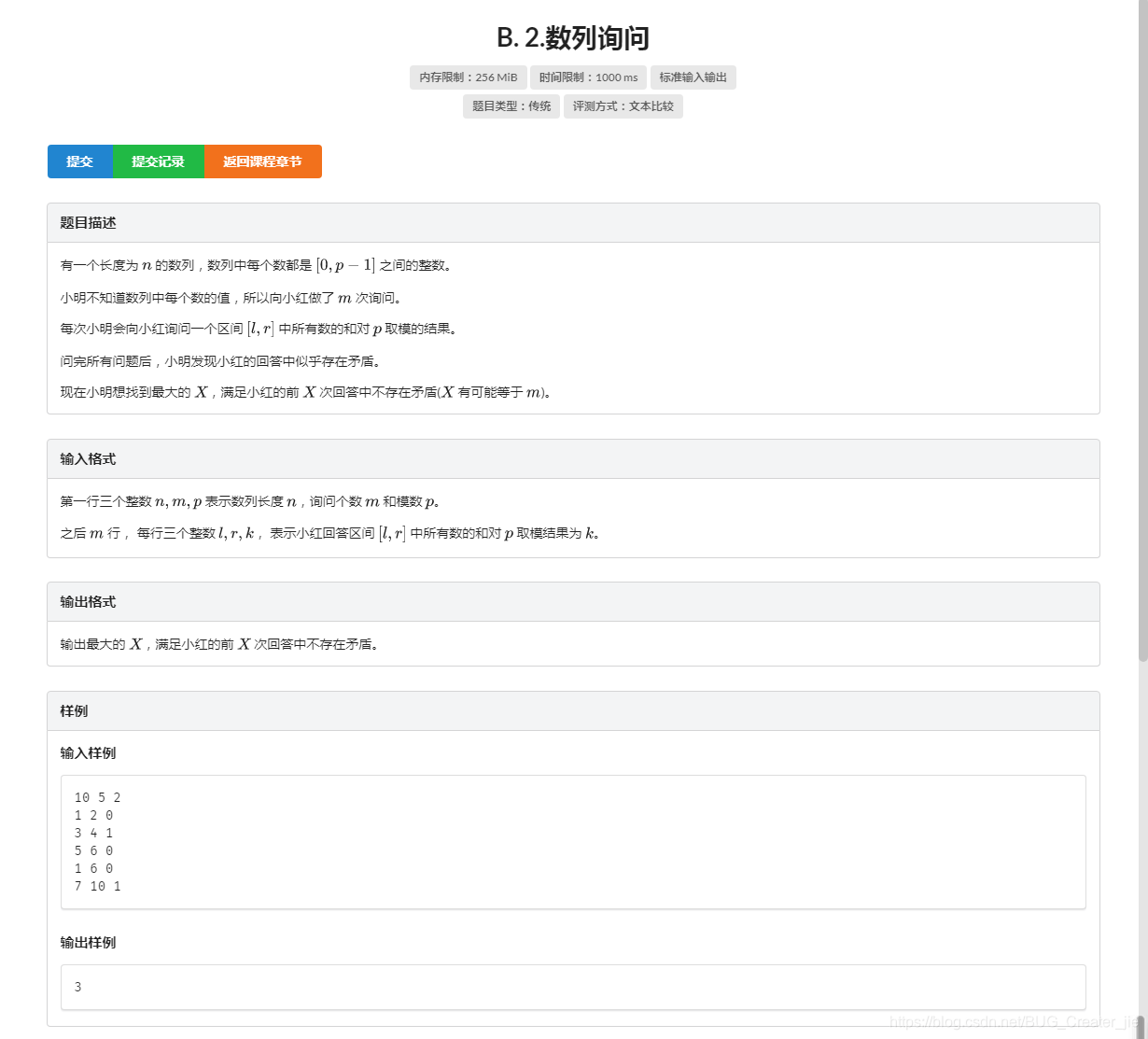
这道题提供了并查集一种新的用处：
合并过程中的状态转移
从前缀和来看：
每次的询问相当于
(sum[r]-sum[l-1])%p=k
我们把l-1合并到r上
fa[i]表示第i个数的父亲结点
num[i]表示 (sum[ fa[i] ] - sum[i])%p的结果
再加上一些奇奇怪怪的状态转移（读者不妨自己推导一下）与判断就ok了~

代码

#include<cmath>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<iostream>
#define ll long long
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
const int N=1e6+100;
const int M=10;
const int mod=100;
int m,n,t,p;
ll ans;
int a,b,c,d;
int num[N],fa[N];
int find(int x){if(fa[x]==x) return x;int ex=fa[x];fa[x]=find(fa[x]);num[x]=(num[ex]+num[x])%p;return fa[x];
}
void merge(int x,int y,int z){int xx=fa[x],yy=fa[y];fa[xx]=yy;num[xx]=(num[y]-num[x]-z+2*p)%p;return;
}
int main(){scanf("%d%d%d",&n,&m,&p);for(int i=1;i<=n;i++) fa[i]=i;for(int i=1;i<=m;i++){scanf("%d%d%d",&a,&b,&c);a--;int aa=find(a),bb=find(b);if(aa==bb){if((num[a]-num[b]+p)%p==c) continue;
//			else if(num[a]==0&&num[b]==c) continue;
//			else if(num[b]==0&&num[a]==c) continue;else{printf("%d",i-1);return 0;}}else{merge(a,b,c);}}printf("%d",m);return 0;
}
/*
10 5 2
1 2 0
3 4 1
5 6 0
1 6 0
7 10 1
*/

二、序列破解（奇偶性）

解析

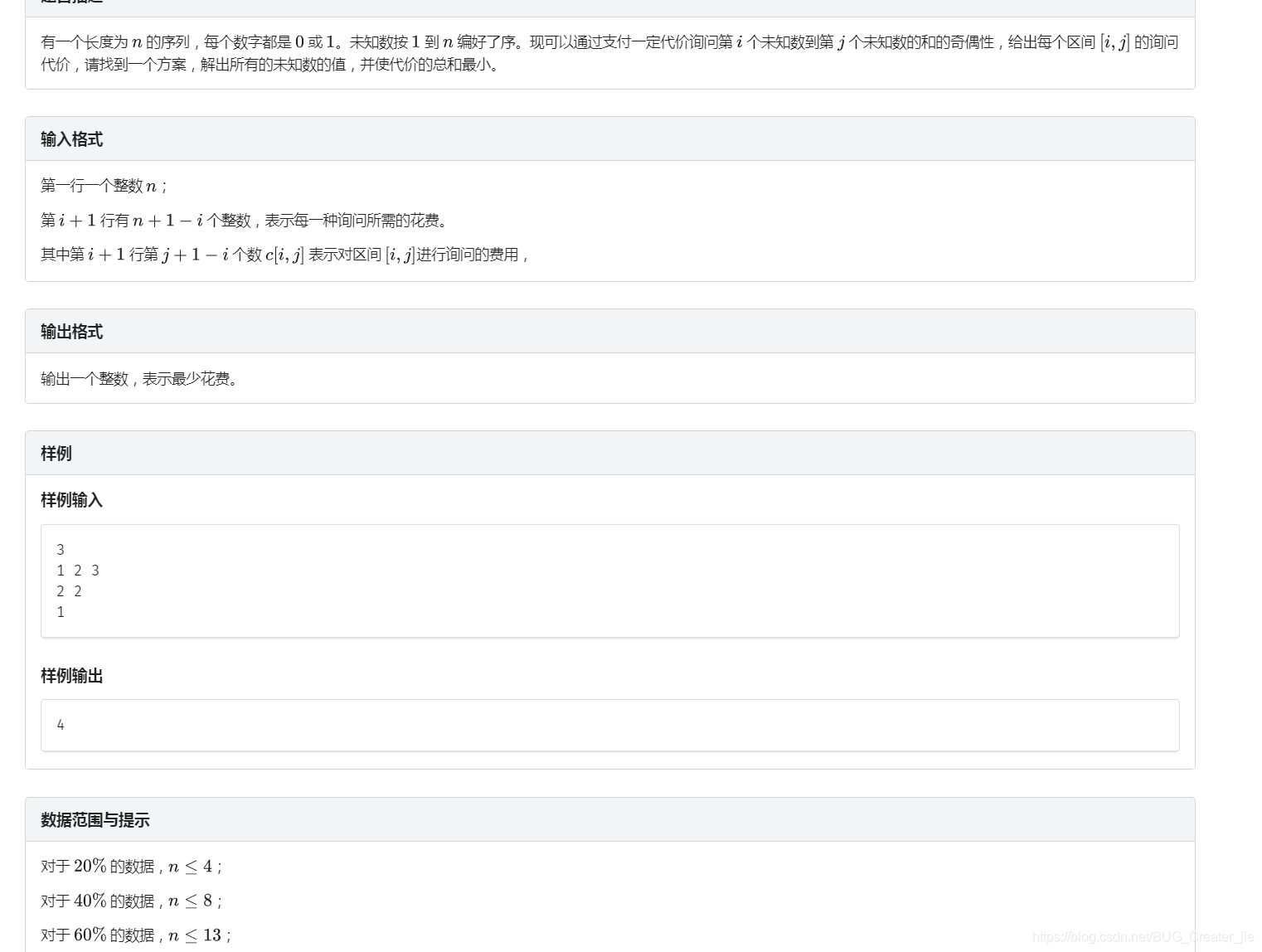
要想知道点k的值，我们必须通过一组[l,k-1]与[l,k]的信息求得；
那么是不是意味着每次对于[l,r]的询问就意味着把点l与点r合并呢？
不是的！
经过推导不难发现：
我们已知[l,r1]和[r1+1,r2]的奇偶性时，才能获得[l,r2]的信息；
而按照刚才的做法，显然是错误的！
所以需要一些微妙的调整
我们发现：
若每次对于[l,r]的询问，把点l-1与r合并，就能使这个问题得到很好的解决
（把点l与r+1合并也可以，是一个道理）
那么我们就只需要保证每个点都与前一个点联通即可
那么显然最后所有的点都会联通
问题就转化为了最小生成树问题

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define mem(a,b) memset(a,b,sizeof(a))
const int N=4e6+100;
int n,m;
int fa[N];
int find(int x){if(fa[x]==x) return x;return fa[x]=find(fa[x]);
}
struct node{int x,y;ll v;bool operator < (const node y)const{return v<y.v;}
}p[N];
int num;
ll ans;
ll a,b,c;
int main(){scanf("%d",&n);for(int i=1;i<=n;i++) fa[i]=i;for(int i=1;i<=n;i++){for(int j=i;j<=n;j++){scanf("%lld",&a);p[++num]=(node){i-1,j,a};	}}sort(p+1,p+1+num);for(int i=1;i<=num&&m<n;i++){int xx=find(p[i].x),yy=find(p[i].y);if(xx==yy) continue;fa[xx]=yy;m++;ans+=p[i].v;}printf("%lld",ans);return 0;
}

thanks for reading！