通俗易懂，C#如何安全、高效地玩转任何种类的内存之Span的脾气秉性(二)

前言

读完上篇《通俗易懂，C#如何安全、高效地玩转任何种类的内存之Span(一)》，相信大家对span的本质应该非常清楚了。含着金钥匙出生的它，从小就被寄予厚望要成为.NET下编写高性能应用程序的重要积木，而且很多老前辈为了接纳它，都纷纷做出了改变，比如String、Int、Array。现在，它长大了，已经成为.NET下发挥关键作用的新值类型。

那我们又该如何接纳它呢？

一句话，熟悉它的脾气秉性，让好钢用到刀刃上。

脾气秉性 - 特点

Slow vs Fast Span

上篇博客介绍了span的本质，主要涉及到三个字段，如下：

640?wx_fmt=png

当我们访问span表示的整体或部分内存时，内部的索引器通过计算(ref reference + byteOffset) + index * sizeOf(T)来正确直接地返回实际储存位置的引用，而不是通过复制内存来返回相对位置的副本，从而达到高性能，但是，现在我要告诉你，这种span被叫做slow span，为什么呢？因为C#7.2的新特性ref T支持在签名中直接返回引用（相当于直接整合了这个过程），这样就无需通过计算来确定指针开头及其起始偏移，从而真正拥有和访问数组一样高的效率，如下：

640?wx_fmt=png

这种只包含两个字段的span就叫Fast span。

在所有的.NET平台，Slow Span都是可得到的，但是目前只有.NET Core 2.X原生支持Fast span。

为了让大家更直观地了解这两种Span，下面来做两组基准测试

不同运行时下Span进行10万次Get、Set的基准测试
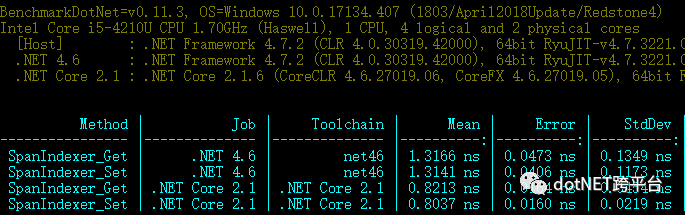
上图非常清楚了吧，从Mean（均值）指标可以看出差异还是比较大的（约60%），net framework时代追求生产力，而core时代追求高性能，所以还是早转core吧，并且新版本core还会进一步优化span，差距将会越来越大。
Span vs Array的基准测试
不同运行时下，对Span和Array进行10万次Get、Set操作
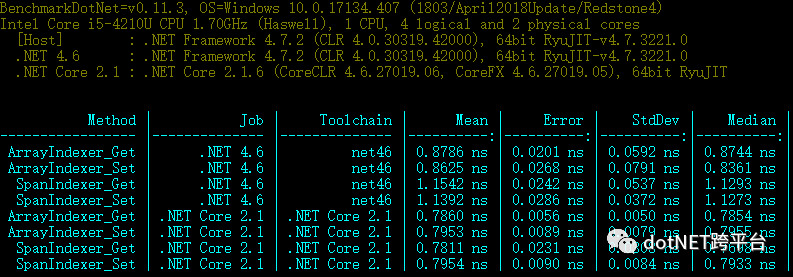
从上图Mean（均值）指标可以得出：
- slow span，即运行时原生不支持，在性能上，它的Get、Set操作和数组差异50%左右。
- fast span，即运行时原生支持，在性能上，它的Get、Set操作和数组相当。

看了上面测试，可能有的同学就会问了用Array就行了，如果总是操作整个数组，这是合适的，但如果想操作数组的一部分数据呢？按照以前的做法每次复制一份相对位置的副本给调用方，这就非常消耗性能的，那么如何支持对完整或部分数组的操作保持同样高的性能呢？答案就是span，没有之一。span不仅能用于访问数组和分离数组子集，还可引用来自内存任意区域的数据，比如本机代码、栈内存、托管内存。

基准测试示例源码参考

Stack-Only

分配一块栈内存是非常快速的，也无需手工释放，它会随着当前作用域而释放，比如方法执行结束时，就自动释放了，所以需要快取快用快放。Span虽然支持所有类型的内存，但决定安全、高效地操作各种内存的下限自然取决于最严苛的内存类型，即栈内存，好比木桶能装多少水，取决于最短的那块木板。此外，上一篇博客的动画非常清晰地演示了span的本质，每次都是通过整合内部指针为新的引用返回，而.NET运行时跟踪这些内部指针的成本非常高昂，所以将span约束为仅存在于栈上，从而隐式地限制了可以存在的内部指针数量。

备注：栈内存的容量非常小， ARM、x86 和 x64 计算机，默认堆栈大小为 1 MB。

所以span必须是值类型，它不能被储存到堆上。

Stack-Only的应用场景

Span不能作为类的字段。
```
class Impossible{Span<byte> field;
}
```
Span不能实现任何接口
先来看一段C#（伪代码）：

640?wx_fmt=png

使用ILDasm查看生成的IL代码：

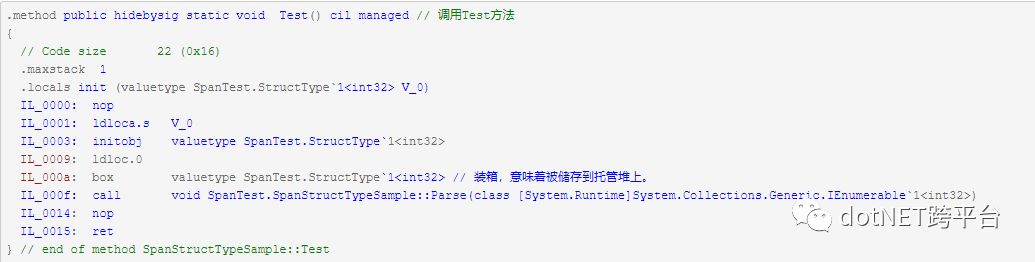
640?wx_fmt=png

上面的代码很明确，首先让自定义的值类型实现接口IEnumerable，然后作为参数传递给Parse，最后分析IL代码发现参数被装箱了，意味着将被储存到托管堆上，如果将来C#能专门定义只用于struct的接口，那么就能扩展Stack-Only结构到此应用场景了，一起期待吧。
Span不能作为异步方法的参数
首先async和await 是非常棒的语法糖，不仅仅大大地简化了编写异步代码的难度，而且还带来了代码的优雅度。
同样，先来看一段C#代码：
```
public async Task TestAsync(Span<byte> data) { }
```
这样的用法也是禁止的，编译时就会报错Parameter or local type Span<byte> cannot be declared in async method.。因为本质上，async & await 的内部是通过AsyncMethodBuilder来创建一个异步的状态机，某一时刻可能会将方法参数储存到托管堆上。
Span不能作为泛型类型的参数
同样，先来看一段C#代码：
```
Func<Span<byte>> valueProvider = () => new Span<byte>(new byte[256]);object value = valueProvider.Invoke(); // 装箱
```
这样的用法也是禁止的，编译时会报错The type Span<byte>may not be used as a type argument.。同理，span<byte>可以表示内存任意区域，而实际使用时肯定需要类型化对象，无法避免装箱。那么微软为什么不引入一种新的泛型约束：stackonly，而是决定禁止span作为泛型参数，因为这需要编译器检查所有的代码，可能还需要理解代码逻辑（因为有的类型需要运行时才能确定），不然是无法保证stackonly约束的，呵呵，目前看来是不现实的，不知人工智能能否解决这个问题。

Stack Tearing

阐述这个特点前，先简单说说计算机的字大小。

计算机的字大小
表示计算机中CPU的字长，32位CPU字长为32位，即4字节；64位CPU字长为64位，即8字节。CPU的字长决定了每次能够原子更新的连续内存块的大小。

栈撕裂其实是多线程下的数据同步问题，当结构数据大于当前处理器的字大小时，都会面临这个问题。如前所述，span内部包含多个字段，这就意味着，一些处理器可能无法保证原子更新span的_reference和_length 字段，也就是说，多线程下_reference和_length可能来自于两个不同的span。

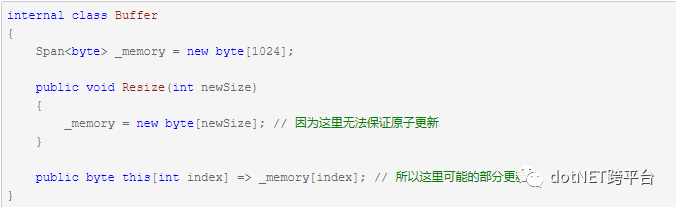
640?wx_fmt=png

其实有两种办法可以解决这个问题：

直接处理 - 加锁，即强制同步访问。
间接处理 - 私有化字段，即不给外面观察到部分更新的机会。

如果这样，就无法保证像数组一样的高性能，因此不能给字段加锁，也不能限制访问（没意义），另外对Span的访问和写入都是直接操作的内存，如果_reference和_length出现不同步的情况，还会导致内存安全问题。

这也是为什么span只能存在于栈上，即指针、数据、长度全都存于栈上，而不是引用存在堆，数据存在栈，因为span<T>不需要暂留，必须快取快用快放，否则就不要使用span。

备注：对于需要暂留到堆上的场景，它的解决方案是Memory<T>，大家可以继续关注。

.NET库的集成

为了支持轻松高效地处理 {ReadOnly}Span ，微软向.NET添加了数百个新成员和类型。目前大多是基于数组、字符串和基元类型的方法的重载，除此之外，还包括一些专注于特定处理方面的全新类型，比如：System.IO.Pipelines。

下面是一些比较常用的扩展：

基元类型（伪代码）

short.Parse(ReadOnlySpan<char> s);

int.Parse(ReadOnlySpan<char> s);

long.Parse(ReadOnlySpan<char> s);
DateTime.Parse(ReadOnlySpan<char> s);
TimeSpan.Parse(ReadOnlySpan<char> input);
Guid.Parse(ReadOnlySpan<char> input);

字符串

public static ReadOnlySpan<char> AsSpan(this string text, int start, int length);

public static ReadOnlySpan<char> AsSpan(this string text, int start);

public static ReadOnlySpan<char> AsSpan(this string text);

数组

public static Span<T> AsSpan<T>(this T[] array, int start);

public static Span<T> AsSpan<T>(this T[] array);

public static Span<T> AsSpan<T>(this ArraySegment<T> segment, int start, int length);

public static Span<T> AsSpan<T>(this ArraySegment<T> segment, int start);

public static Span<T> AsSpan<T>(this T[] array, int start, int length);

最后使用上面的API演示一个官网的例子，解析字符串"123,456"中的数字：

以前的写法：

var input = "123,456";
var commaPos = input.IndexOf(',');
var first = int.Parse(input.Substring(0, commaPos));
// yes-Allocating, yes-Coping
var second = int.Parse(input.Substring(commaPos + 1));
// yes-Allocating, yes-Coping

现在的写法：

var input = "123,456";
var inputSpan = input.AsSpan();
var commaPos = input.IndexOf(',');
var first = int.Parse(inputSpan.Slice(0, commaPos));
// no-Allocating, no-Coping
var second = int.Parse(inputSpan.Slice(commaPos + 1));
// no-Allocating, no-Coping

当然还是有许多这样的方法，比如System.Random、System.Net.Socket、Utf8Formatter、Utf8Parser等，明白了它的脾气秉性，对于具体的应用场景大家可以先自行查阅资料，相信认真读完上篇、本篇的同学已经具备用好这把尖刀的能力了。

总结

本篇在上篇（理解span的本质）的基础上，详细讲解span的特点和每种特点下的应用场景，希望大家能有所收获。下一篇可能会讲span的加强，以及在数据转换方面的应用，比如：Data Pipelines、Discontinuous Buffers、Buffer Pooling等，也可能会讲Memory<T>，看到时候的准备吧，感兴趣请继续关注。