程序员修仙之路--把用户访问记录优化到极致

点击上方蓝色字体，关注我们

菜菜呀，前几天做的用户空间，用户反映有时候比较慢呀

CEO,CTO,CFO于一身的CXO 640?wx_fmt=gif

是吗？

菜菜

我把你拉进用户反馈群，你解决一下呀

CEO,CTO,CFO于一身的CXO 640?wx_fmt=gif

（完了，以后没清净时候了）我尽量吧，X总，我涨工资的事.....

菜菜

这不来年底了吗，年会奖品可是很丰厚的，希望你抽个一等奖呀，你先出去吧！

CEO,CTO,CFO于一身的CXO 640?wx_fmt=gif

.........,那答应的年终奖的事？

菜菜

不是给你发了200元的京东卡吗

CEO,CTO,CFO于一身的CXO 640?wx_fmt=gif

.............转身默默离开，羊驼慢慢飘过....

菜菜

祝愿大家不要像菜菜这般苦逼，年中奖大大滴！！！

在没有年终奖的日子里，工作依然还要继续.....一张冰与火的图尽显无奈

还记得菜菜不久之前设计的用户空间吗？没看过的同学请进传送门=》设计高性能访客记录系统

还记得遗留的什么问题吗？菜菜来重复一下，在用户访问记录的缓存中怎么来判断是否有当前用户的记录呢？链表虽然是我们这个业务场景最主要的数据结构，但并不是当前这个问题最好的解决方案，所以我们需要一种能快速访问元素的数据结构来解决这个问题？那就是今天我们要谈一谈的 散列表

散列表

散列表（Hash table，也叫哈希表），是根据关键码值(Key value)而直接进行访问的数据结构。也就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做散列函数，存放记录的数组叫做散列表

散列表其实可以约等于我们常说的Key-Value形式。散列表用的是数组支持按照下标随机访问数据的特性，所以散列表其实就是数组的一种扩展，由数组演化而来。可以说，如果没有数组，就没有散列表。为什么要用数组呢？因为数组按照下标来访问元素的时间复杂度为O（1），不明白的同学可以参考菜菜以前的关于数组的文章。既然要按照数组的下标来访问元素，必然也必须考虑怎么样才能把Key转化为下标。这就是接下来要谈一谈的散列函数。

散列函数

散列函数通俗来讲就是把一个Key转化为数组下标的黑盒。散列函数在散列表中起着非常关键的作用。散列函数，顾名思义，它是一个函数。我们可以把它定义成hash(key)，其中 key 表示元素的键值，hash(key) 的值表示经过散列函数计算得到的散列值。

那一个散列函数有哪些要求呢？

1. 散列函数计算得到的值是一个非负整数值。

2. 如果 key1 = key2，那hash(key1) == hash(key2)

3. 如果 key1 ≠ key2，那hash(key1) ≠ hash(key2)

简单说一下以上三点，第一点：因为散列值其实就是数组的下标，所以必须是非负整数（>=0），第二点：同一个key计算的散列值必须相同。重点说一下第三点，其实第三点只是理论上的，我们想象着不同的Key得到的散列值应该不同，但是事实上，这一点很难做到。我们可以反证一下，如果这个公式成立，我计算无限个Key的散列值，那散列表底层的数组必须做到无限大才行。像业界比较著名的MD5、SHA等哈希算法，也无法完全避免这样的冲突。当然如果底层的数组越小，这种冲突的几率就越大。所以一个完美的散列函数其实是不存在的，即便存在，付出的时间成本，人力成本可能超乎想象。

散列冲突

既然再好的散列函数都无法避免散列冲突，那我们就必须寻找其他途径来解决这个问题。

1. 寻址

如果遇到冲突的时候怎么办呢？方法之一是在冲突的位置开始找数组中空余的空间，找到空余的空间然后插入。就像你去商店买东西，发现东西卖光了，怎么办呢？找下一家有东西卖的商家买呗。不管采用哪种探测方法，当散列表中空闲位置不多的时候，散列冲突的概率就会大大提高。为了尽可能保证散列表的操作效率，一般情况下，我们会尽可能保证散列表中有一定比例的空闲槽位。我们用装载因子（load factor）来表示空位的多少。

散列表的装载因子 = 填入表中的元素个数 / 散列表的长度

装载因子越大，说明空闲位置越少，冲突越多，散列表的性能会下降. 假设散列函数为 f=(key%1000),如下图所示

2. 链地址法（拉链法）

拉链法属于一种最常用的解决散列值冲突的方式。基本思想是数组的每个元素指向一个链表，当散列值冲突的时候，在链表的末尾增加新元素。查找的时候同理，根据散列值定位到数组位置之后，然后沿着链表查找元素。如果散列函数设计的非常糟糕的话，相同的散列值非常多的话，散列表元素的查找会退化成链表查找，时间复杂度退化成O（n）

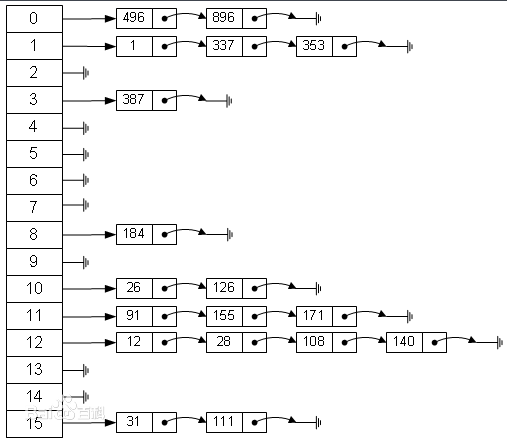
3. 再散列法

这种方式本质上是计算多次散列值，那就必然需要多个散列函数，在产生冲突时再使用另一个散列函数计算散列值，直到冲突不再发生，这种方法不易产生“聚集”，但增加了计算时间。

4. 建立一个公共溢出区

至于这种方案网络上介绍的比较少，一般应用的也比较少。可以这样理解：散列值冲突的元素放到另外的容器中，当然容器的选择有可能是数组，有可能是链表甚至队列都可以。但是无论是什么，想要保证散列表的优点还是需要慎重考虑这个容器的选择。

扩展阅读

1. 这里需要在强调一次，散列表底层依赖的是数组按照下标访问的特性（时间复杂度为O(1）），而且一般散列表为了避免大量冲突都有装载因子的定义，这就涉及到了数组扩容的特性：需要为新数组开辟空间，并且需要把元素copy到新数组。如果我们知道数据的存储量或者数据的大概存储量，在初始化散列表的时候，可以尽量一次性分配足够大的空间。避免之后的数组扩容弊端。事实证明，在内存比较紧张的时候，优先考虑这种一次性分配的方案也要比其他方案好的多。

2. 散列表的寻址方案中，有一种特殊情况：如果我寻找到数组的末尾仍然无空闲位置，怎么办呢？这让我想到了循环链表，数组也一样，可以组装一个循环数组。末尾如果无空位，就可以继续在数组首位继续搜索。

3. 关于散列表元素的删除，我觉得有必要说一说。首先基于拉链方式的散列表由于元素在链表中，所有删除一个元素的时间复杂度和链表是一样的，后续的查找也没有任何问题。但是寻址方式的散列表就不同了，我们假设一下把位置N元素删除，那N之后相同散列值的元素就搜索不出来了，因为N位置已经是空位置了。散列表的搜索方式决定了空位置之后的元素就断片了....这也是为什么基于拉链方式的散列表更常用的原因之一吧。

4. 在工业级的散列函数中，元素的散列值做到尽量平均分布是其中的要求之一，这不仅仅是为了空间的充分利用，也是为了防止大量的hashCode落在同一个位置，设想在拉链方式的极端情况下，查找一个元素的时间复杂度退化成在链表中查找元素的时间复杂度O（n），这就导致了散列表最大特性的丢失。

5. 拉链方式实现的链表中，其实我更倾向于使用双向链表，这样在删除一个元素的时候，双向链表的优势可以同时发挥出来，这样可以把散列表删除元素的时间复杂度降低为O（1）。

6. 在散列表中，由于元素的位置是散列函数来决定的，所有遍历一个散列表的时候，元素的顺序并非是添加元素先后的顺序，这一点需要我们在具体业务应用中要注意。

640?wx_fmt=gif

Net Core c# 代码

有几个地方菜菜需要在强调一下：

1. 在当前项目中用的分布式框架为基于Actor模型的Orleans，所以我每个用户的访问记录不必担心多线程问题。

2. 我没用使用hashtable这个数据容器，是因为hashtable太容易发生装箱拆箱的问题。

3. 使用双向链表是因为查找到了当前元素，相当于也查找到了上个元素和下个元素，当前元素的删除操作时间复杂度可以为O(1)

 class UserViewInfo
    {
        //用户ID
        public int UserId { get; set; }
        //访问时间，utc时间戳
        public int Time { get; set; }
        //用户姓名
        public string UserName { get; set; }
    }

class UserSpace
    {
        //缓存的最大数量
        const int CacheLimit = 1000;
        //这里用双向链表来缓存用户空间的访问记录
        LinkedList<UserViewInfo> cacheUserViewInfo = new LinkedList<UserViewInfo>();
        //这里用哈希表的变种Dictionary来存储访问记录，实现快速访问，同时设置容量大于缓存的数量限制，减小哈希冲突
        Dictionary<int, UserViewInfo> dicUserView = new Dictionary<int, UserViewInfo>(1250);

        //添加用户的访问记录
        public void AddUserView(UserViewInfo uv)
        {
            //首先查找缓存列表中是否存在，利用hashtable来实现快速查找
            if (dicUserView.TryGetValue(uv.UserId, out UserViewInfo currentUserView))
            {
                //如果存在，则把该用户访问记录从缓存当前位置移除，添加到头位置
                cacheUserViewInfo.Remove(currentUserView);
                cacheUserViewInfo.AddFirst(currentUserView);
            }
            else
            {
                //如果不存在，则添加到缓存头部 并添加到哈希表中
                cacheUserViewInfo.AddFirst(uv);
                dicUserView.Add(uv.UserId, uv);
            }
            //这里每次都判断一下缓存是否超过限制
            if (cacheUserViewInfo.Count > CacheLimit)
            {
                //移除缓存最后一个元素，并从hashtable中删除,理论上来说，dictionary的内部会两个指针指向首元素和尾元素，所以查找这两个元素的时间复杂度为O（1）
                var lastItem = cacheUserViewInfo.Last.Value;
                dicUserView.Remove(lastItem.UserId);
                cacheUserViewInfo.RemoveLast();
            }
        }
    }