Hawk是一款开源图形化的爬虫和数据清洗工具，GitHub Star超过2k+，前几代版本介绍如下：

Hawk3: 终于等到你: 图形化开源爬虫Hawk 3发布!

Hawk2: 120项优化: 超级爬虫Hawk 2.0重磅发布！

Hawk1: 如何从互联网采集海量数据？租房,二手房,薪酬…

Hawk从2015年开源，但Hawk5则带来了其历史上最大的更新，解决诸多bug，提供开放的任务市场，手机app嗅探和更强大的调试系统。 因此我们直接跳过Hawk4,发布Hawk5。

那么Hawk5带来哪些让人兴奋的更新呢？ 大招在最后！

Hawk5对界面做了进一步的完善和微调，使用更人性化：

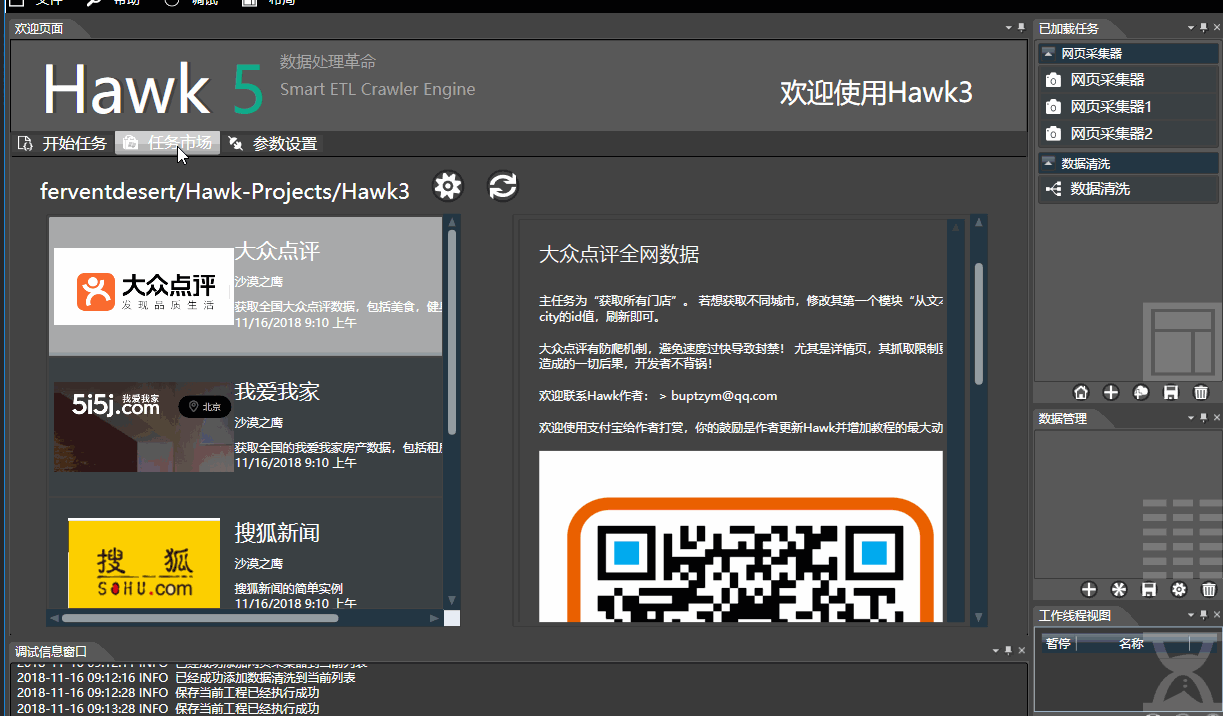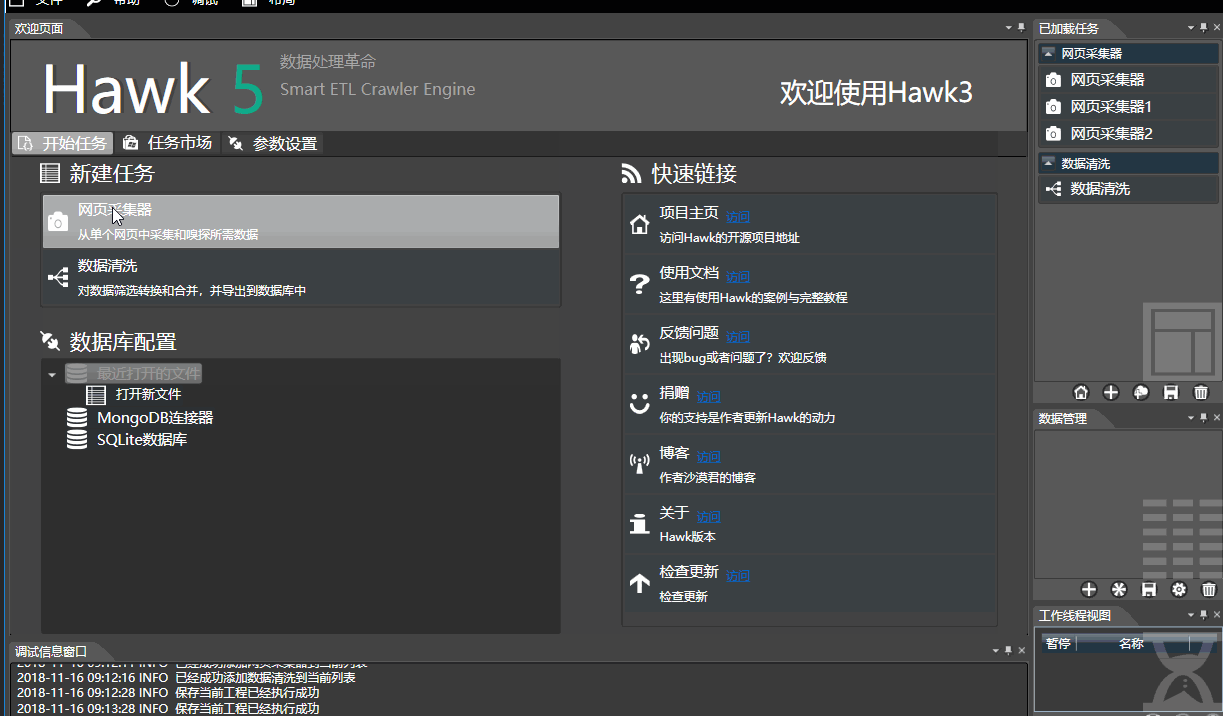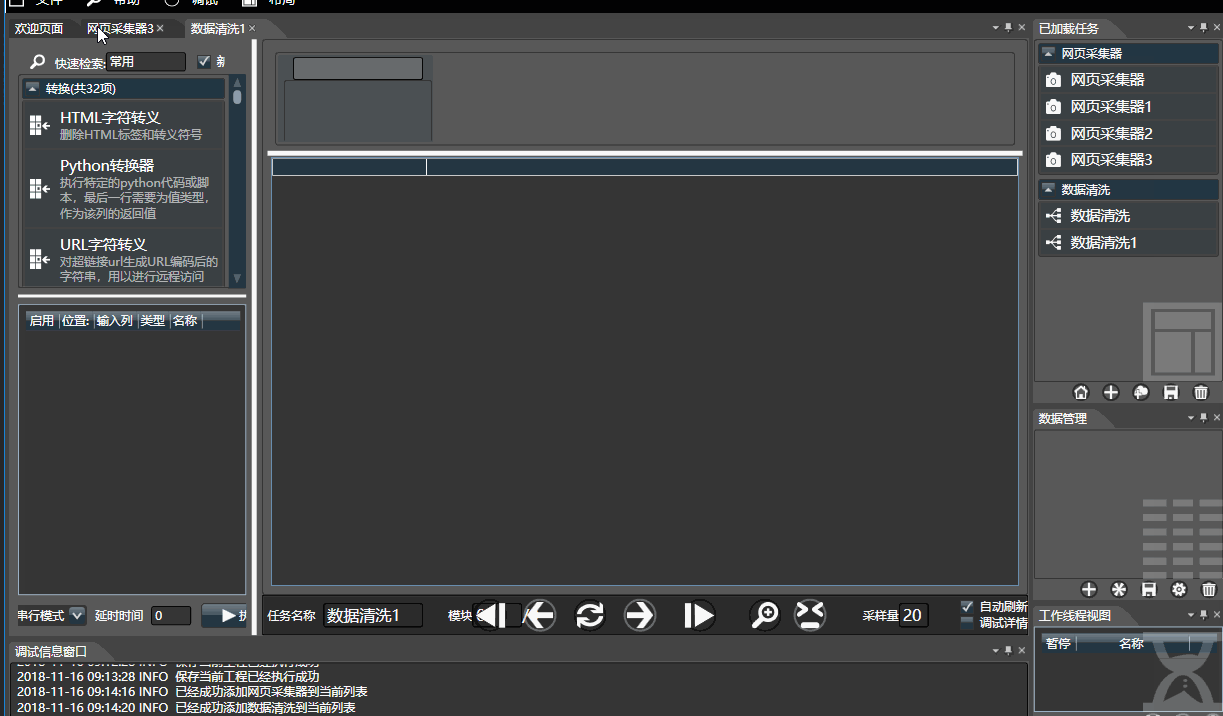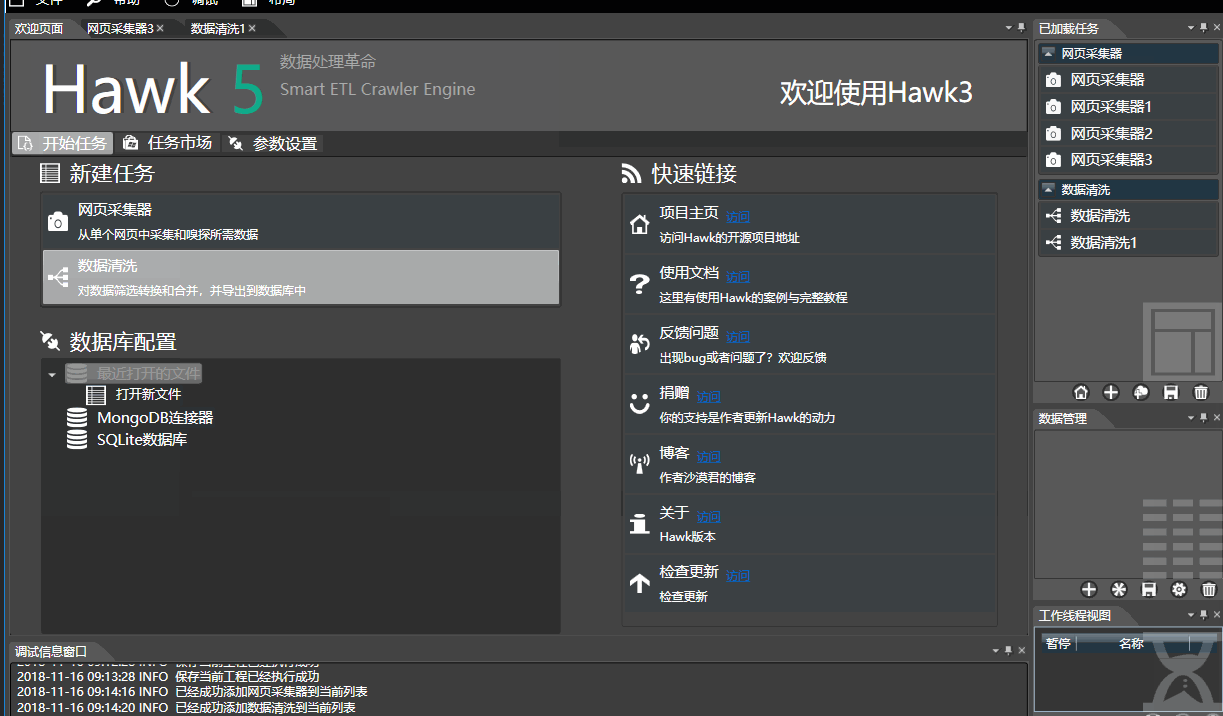
断点续跑和自动保存

Hawk早期版本不稳定，用户正在编辑任务或处理数据时，Hawk扑街了！

Hawk5能自动保存任务，数据表，甚至当前执行的位置！一旦关闭或崩溃，不要怕!数据一条没丢，重启后，还能从上次中断继续运行！就像断点续传一样，颤抖吧筒子们！

自动回补数据

这是另一革命性功能，由于访问网站经常会超时或不可访问，想一次性抓取且不重不漏是非常困难的。

Hawk5支持批量补数据。当发生异常时，Hawk会将异常和上下文写入数据表，之后即可智能重新执行，将数据不重不漏地回补回来。

丰富的文档，自动更新和多国语言

Hawk5中，帮助文档获得了极大的增强，除了丰富和细致的在线文档之外：

https://ferventdesert.github.io/Hawk/

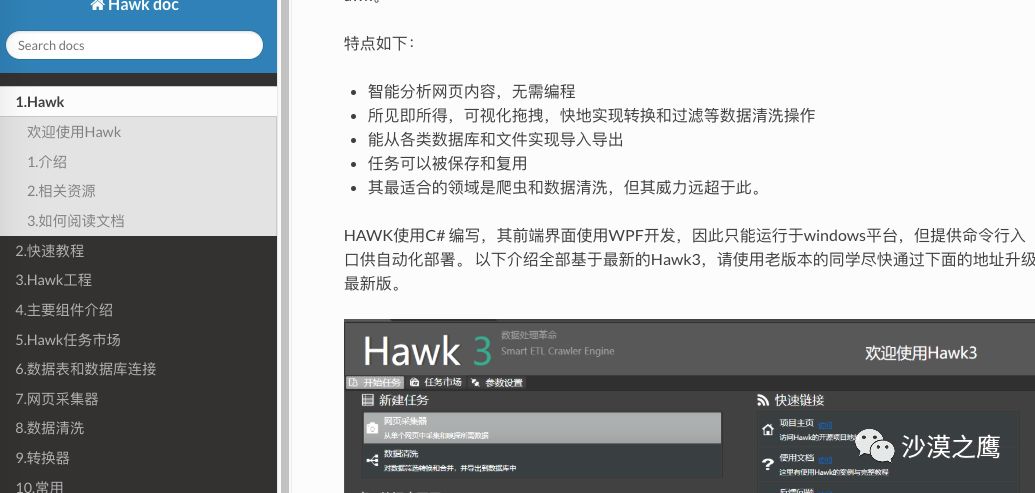
还在各个模块下方提供图文并茂的说明，当你不知道该按钮的作用时，鼠标放在该按钮上保持3秒就有贴心提示出现！

更贴心的是，设计完任务后，一键即可生成手把手帮助文档。新手按部就班即可重现该任务！

Hawk5进一步地提供了多国语言，能方便地在中文，English或其他任何语言切换，只要在执行目录增加对应的语言文件即可。

同时，Hawk的自动更新机制，能够让迭代更加敏捷，有新版本的Hawk即可一键更新，妈妈再也不用担心Hawk出现bug了！

全局参数

早期的Hawk，多任务间协同比较复杂，子任务也不能彻底解决该问题。

Hawk5中提供了全局参数系统，可以在任何模块中，使用大括号引用你已经配置的参数，并能在多个参数组间切换。

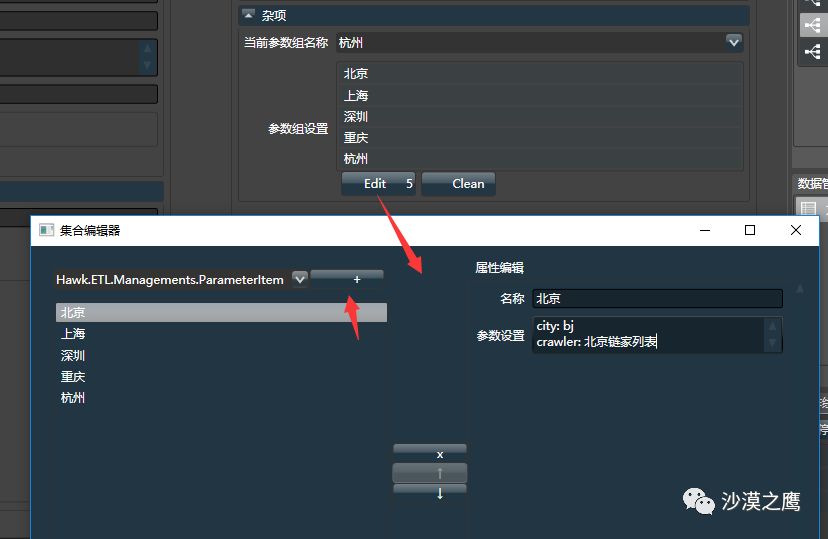
这有什么用呢？举个栗子，当二手房抓取时，每个城市们页面格式和地址都不相同， 需要手工切换多个参数。使用全局参数后，切换配置组即可一键在不同城市间切换！

调试系统和UI交互改进

早期Hawk在配置错误时，一条数据都出不来，卡住的不仅是Hawk，还有用户的心。

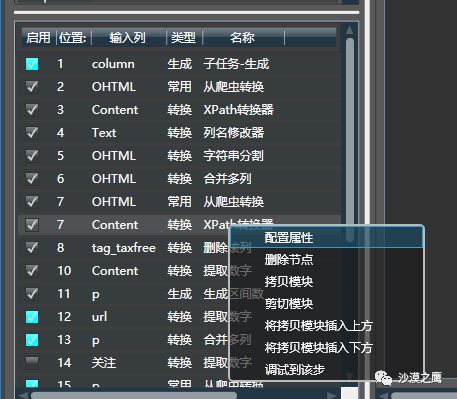
Hawk5提供了更加方便的调试系统，每个模块是否正常工作，会以绿色方格提醒，一目了然。当任务的某个模块出现异常时会及时提示。

超级拷贝，可以通过shift键，选择多个模块，在多个任务间拷贝。你甚至还能将Hawk自动嗅探出的网页XPath结构一键拷贝为python代码，极大地简化爬虫工程师的工作！

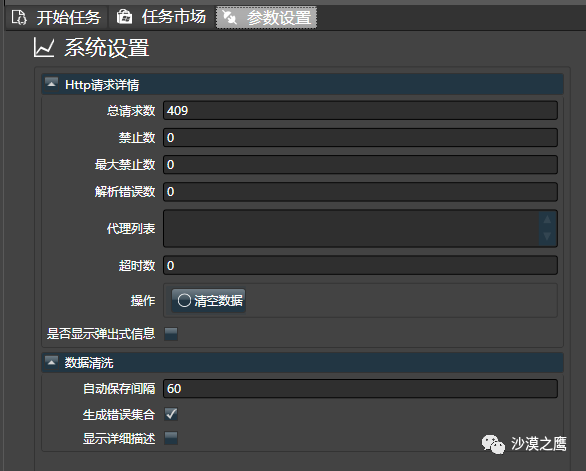
是否已经被网站封锁？总共进行了多少次请求？全局统计系统能够方便的显示当前总的web请求数，异常数，超时数，当错误数达到阈值时，更能自动暂停所有的任务！

除此之外，新版的Hawk更是改进了UI设计，例如XPath转换器，能够通过关键字快速定位，几次点选即可获取真实XPath。

社会化协作：任务市场

以前所有的Hawk用户只能各自为政，无法共享和沟通。

在新的Hawk中，你可以浏览任务市场，直接加载远程任务和浏览数据，并方便地组合其他人的任务。像BT站一样，作者发布数据清洗工程后，所有的Hawk用户就会立即受益！

以前想抓取全国二手房很复杂，且不能应对网站改版。在Hawk市场只要轻轻点击加载任务即可，所见即所得，一键将数据导出到Excel。

这是Hawk本次更新的最重要的功能，它极大地改善了Hawk社会化协作，基于GitHub。由于账号系统的限制，目前还不能在软件中直接上传任务（未来会提供），如果你希望向主仓库贡献任务，可提交git的pull request。

在AI时代，通过大量用户使用Hawk的行为和任务市场的积累，我们能够通过强化学习等技术，自动让AI学出数据清洗和转换算法，让Hawk变得更加智能。

无限想象：自动抢票，翻译，图片识别…

如果你只以为Hawk就是个爬虫，那就错了，Hawk是个通用的流式计算客户端。未来Hawk市场，不仅会有共享的任务，更会引入第三方插件机制，极大地扩展Hawk流式计算的版图。

目前正在开发中的浏览器驱动插件，能够让Hawk自动控制浏览器，模拟点击，翻页等一系列操作，你要做的只是做一遍后导入到Hawk。通过配置数据清洗流，能够实现自动抢票，键盘输入等一系列功能。

Hawk5的手机远程嗅探功能，能方便的抓取手机app的数据，相关教程会在近期放出。

未来的插件能够更方便地调用百度识图，翻译转换以及各类服务存储API，让更多用户能够通过Hawk拖拽就能实现丰富的数据处理，并导出成任何格式。

我们对Hawk的理念，是开源，去中心化和社会化协作。它没有公司去运营，没有中心服务器，只依赖了免费的GitHub仓库，使用文档和教程都是机器自动生成的。但它也在各种艰难中一路走来，但我们对Hawk的愿景，是让数据流变得更加智能，让数据工作者变得更加地敏捷方便。

感谢阅读，点击原文链接，直达Hawk文档。如果Hawk给你提供了帮助，欢迎转发本文给更多的朋友，并欢迎给本项目的GitHub点个star!