最近在做公司的项目的时候，开始把部分程序迁移到EF Core，然后有了一些感触，趁着还没忘却，还是先记录下来。

EF Core还在成长中，我写这个的时候，版本是2.2。如果对着已有的EF 5/6来说，还有很多功能要迎头赶上的，所以这个也是为什么在.net core 3的标准中，计划要支持EF 6（这个其实是一次性买卖），就是想让大家可以先把.net Core (EF6)用起来，让EF Core先缓口气，等它成长足够了，再迁移到.net Core (EF Core)这样的组合。

即便如此，现在版本的EF Core已经有好多不少的闪亮之处（当然也有一些会因为自己没学好而误会了它的坑）。不论是闪亮点，还是坑，我有时间的话，会缓缓道来。

Shadow Properties这个特性很好，值得先拿出来说一下。但是博客本来就不适宜写得长，不然就不适合碎片阅读。所以我会把它分开来写。而且我还可能会比较啰嗦，有骗字数的嫌疑。

Shadow properties are properties that are not defined in your .NET entity class but are defined for that entity type in the EF Core model. The value and state of these properties is maintained purely in the Change Tracker. (https://docs.microsoft.com/en-us/ef/core/modeling/shadow-properties)

简单地说，隐藏属性 (Shadow Properties)，就是那些逻辑设计里面没有的，但是物理设计里面却要有的属性。逻辑设计 vs. 物理设计，是做面向对象编程的攻城狮，都需要面对的问题。例如，那些数据库自增长的ID，审计类字段，还有例如做数据库订阅所需要的时间戳等等。很绕口，让我说人话，就是我们的business class（业务类），是不会包括那些只对照某数据库，或者中间件才冒出来的神马ID之类的属性，而我们却可以在EF Core层面，搞定这些ID的安置方式，而不需要另外再弄一个新的EF class。

有了这个，我们就可以保持逻辑设计的干净，也可以省了再去多弄一个EF Class。或者干脆就着EF Class来细细捣弄（为了继续保持逻辑层的干净）。后述的两种手法，在我们灵活运用EF 5/6的时候，已经屡见不鲜了。

简单举个几个栗子（边幅所限，本篇先来一个个简单的，后面的继续举拖沓的栗子，继续骗字数）。例如，我们会在数据库有一些 LastUpdateBy （记录最后修改者/兼顾新增此记录建立者）、LastUpdateDate（记录最后改动的日期和时间）、CreatedDate（新增此记录的日期和时间）等等，提供简单审计记录功能的字段。但是，我们的Class里面，真心不想要这些属性。这个时候，我们可以继续保持原有business class不变。而在我们的DBContext class的OnModuleCreating方法中，针对某个需要有上述审计字段的Entity，加上这些Shadow Properties。下面的代码片段的例子，只支持UpdateDate和UpdateBy，CreateDate请自行脑补哈(Tips: EntityState.Added 状态下才更新此属性的值)。

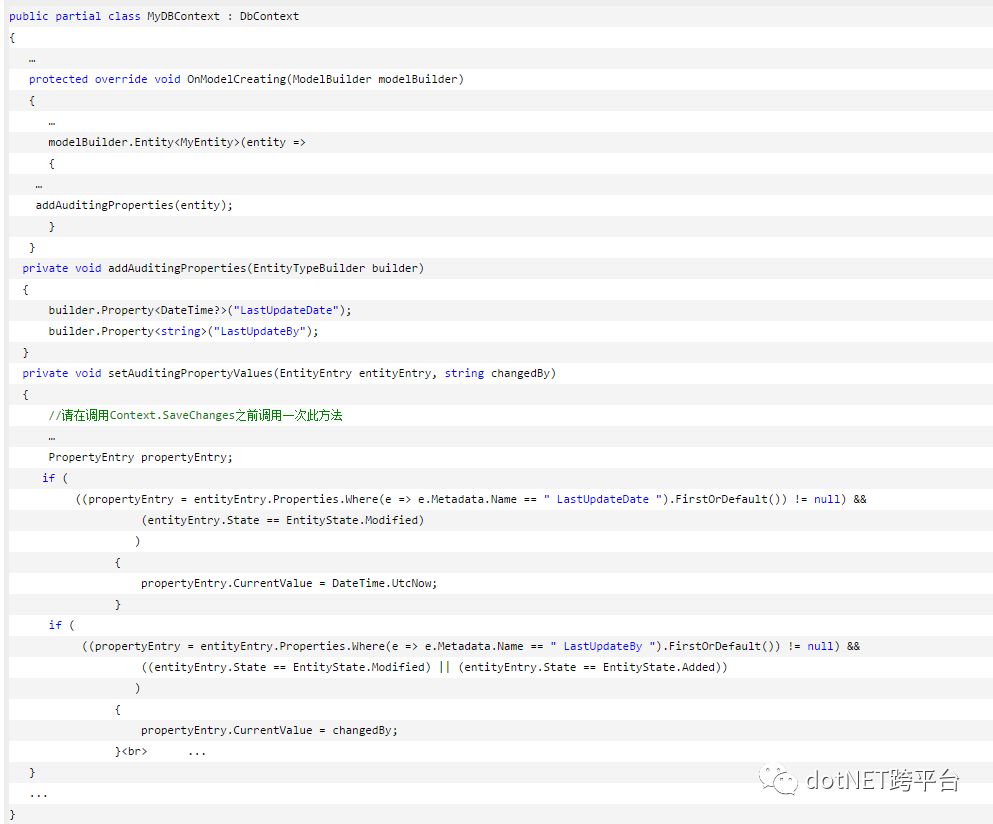
 很简单对吧？只需要偷偷地在自己的DBContext里面捣弄一下，根本不需要让上层建筑知道那么多，我们就支持了仅在数据表里面才有的审计类字段。

接下来，下一篇，会举一个更啰嗦的栗子。解释一下，为什么我们的business class，不应该有那些由于物理设计（落地选型）所带出来的各式各样的神马ID，以及怎么用Shadow Properties来支持。但是因为这个涉及到asp.net core web api的相应改动，所以值得另开一个帖子来骗字数了。

原文地址:

https://www.cnblogs.com/fatkent/p/EFCore_ShadowProperties_1.html

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com