[LOJ 6042]「雅礼集训 2017 Day7」跳蚤王国的宰相

description

solution

一个到所有节点距离和最小的节点 $\iff$ 树的重心（满足最重的儿子最轻，每个儿子siz$\le \frac{n}{2}$）

显然原树的重心答案为0

对于点$i$，若要成为新的重心

贪心地有，从原重心的最大儿子边开始断，然后直接接在$i$上

此时把$i$提起来当根，则有原来的子树仍不变，断掉的若干个子树接在下面，剩下的所有点为一个子树

如果原重心断的子树节点达到/超过$\frac{n}{2}$，则一定是可以使任意一个$i$成为新重心的（剩下节点数不到一半，符合重心设定）

最后的答案一定是$cnt/cnt-1,cnt$表示重心断的子树个数

1的出入是因为有些点可能自己的$siz$足够大，不需要断这么多

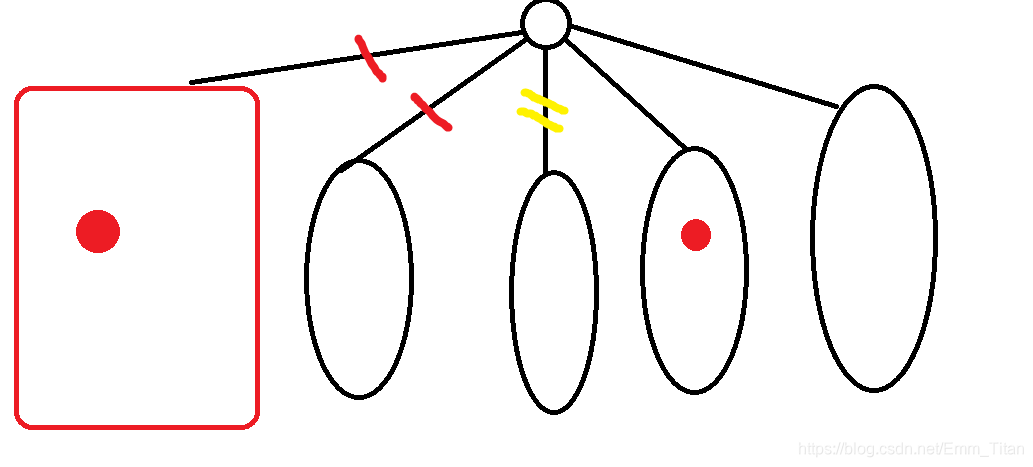
如图：红边，黄边为被断子树(黄边为最后一个被断子树)

• $i$属于被断子树内（第一个红点）

  先不断这个子树，断另外的cnt-1个子树，此时需要判断总点数$n-$其子树$siz[i]-$断掉的子树$used=$剩下的子树是否$>\frac{n}{2}$，超过再断$i$所在$root$的子树

• $i$属于残留子树（第二个红点）

  先不断第cnt被断子树（这样剩下连在一起的子树节点才最小，才更有可能少断一条边），同样的判断

code

#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
#define maxn 1000005
vector < int > G[maxn];
int n, rt, minn, cnt;
int siz[maxn], ans[maxn];void dfs( int u, int fa ) {siz[u] = 1;int max_size = 0;for( int i = 0;i < G[u].size();i ++ ) {int v = G[u][i];if( v == fa ) continue;else dfs( v, u );siz[u] += siz[v];max_size = max( max_size, siz[v] );}max_size = max( max_size, n - siz[u] );if( max_size < minn ) {minn = max_size;rt = u;}
} int GetRoot() {minn = 0x7f7f7f7f;dfs( 1, 0 );return rt;
}bool cmp( const int x, const int y ) {return siz[x] > siz[y];
}void solve( int u, int fa, int used ) {ans[u] = cnt + ( ( ( n - siz[u] - used ) << 1 ) > n );for( int i = 0;i < G[u].size();i ++ ) {int v = G[u][i];if( v == fa ) continue;else solve( v, u, used );}
}int main() {scanf( "%d", &n );for( int i = 1, u, v;i < n;i ++ ) {scanf( "%d %d", &u, &v );G[u].push_back( v );G[v].push_back( u );}int root = GetRoot();dfs( root, 0 );sort( G[root].begin(), G[root].end(), cmp );int tot = 0;for( int i = 0;i < G[root].size();i ++ ) {tot += siz[G[root][i]];if( ( tot << 1 ) >= n ) break;cnt ++;}for( int i = 0;i < G[root].size();i ++ )solve( G[root][i], root, tot - max( siz[G[root][i]], siz[G[root][cnt]] ) );for( int i = 1;i <= n;i ++ )printf( "%d\n", ans[i] );return 0;
}