基环树的常见解法

• 若干个基环树互相独立
• 断环为链（随便断一条）
• 环外树和环外树之间的树形DP
• 环变链后整体可以用数据结构简单维护操作

[ZJOI2008]骑士

luogu2607

每个人都有讨厌的人，将这个条件转换成两人之间存在一条边

原图则转换成了若干个互不干扰的基环树

单独考虑一棵基环树

对于“树”的部分，可以树形$DP$

对于“环”的部分，不用单调队列，直接随便找一条环上边，强制断开

基环树就彻底变成了一棵树

设计$d{p}_{u,0/1}$转移

• 父亲选，则所有儿子不能选
• 父亲不选，则儿子可选可不选
• 儿子之间也是互相独立的

分别以断开的边的两端作为树根，最后就是max(dp[S][0], dp[T][0])

为什么没有dp[S][1],dp[T][1]？

• 以S为例，dp[S][0]是S为树根时强制不选的最大值
• 此时$T$是树中一个节点，会根据转移方程式决定T是否选择
• 如果dp[S][0]是不含$T$的，说明最佳方案本来就是S,T都不选择
• 所以就不能出现dp[S][1]，最佳方案可能包含了T
• dp[T][0]同理

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define int long long 
#define maxn 1000005
int n, cnt, S, T, ID;
int w[maxn], head[maxn], to[maxn << 1], nxt[maxn << 1];
int dp[maxn][2];
bool vis[maxn];void addedge( int u, int v ) {to[cnt] = v, nxt[cnt] = head[u], head[u] = cnt ++;to[cnt] = u, nxt[cnt] = head[v], head[v] = cnt ++;
}void dfs1( int u, int id ) {vis[u] = 1;for( int i = head[u];~ i;i = nxt[i] ) {if( i == id ) continue;int v = to[i];if( vis[v] ) {S = u, T = v, ID = i;continue;}else dfs1( v, i ^ 1 );}
}void dfs2( int u, int id ) {dp[u][0] = 0, dp[u][1] = w[u];for( int i = head[u];~ i;i = nxt[i] ) {if( i == id or i == ID or i == ( ID ^ 1 ) ) continue;int v = to[i];dfs2( v, i ^ 1 );dp[u][0] += max( dp[v][0], dp[v][1] );dp[u][1] += dp[v][0];}
}signed main() {memset( head, -1, sizeof( head ) );scanf( "%lld", &n );for( int i = 1, x;i <= n;i ++ ) {scanf( "%lld %lld", &w[i], &x );addedge( i, x );}int ans = 0;for( int i = 1;i <= n;i ++ ) {if( vis[i] ) continue;dfs1( i, -1 );int t = 0;dfs2( S, -1 ); t = max( t, dp[S][0] );dfs2( T, -1 ); t = max( t, dp[T][0] );ans += t;}printf( "%lld\n", ans );return 0;
}

[IOI2008] Island

luogu4381

同样的，这是相互独立的若干棵基环树

问题转化为求若干个基环树的直径之和

单独考虑一个基环树，设计状态转移方程

边权变成入点的点权

$f_i:i$子树内以$i$为链端的最长链长度

$g_i:i$子树内的直径

首先可以利用拓扑做有向图，求出所有的环，顺便转移出每个点的信息

• $v\in so{n}_u$
• 直径是$v$子树内的直径
  • $g_u=\max (g_u,g_v)$
• 直径是由$u$的两条链拼接而成，其中一条链过$v$
  • $g_u=\max (f_u+f_v+w_{u,v},g_u)$
• 最长链为$v$这一条链
  • $f_u=\max (f_u,f_v+w_{u,v})$

考虑环上的点信息更新

• 基环树直径可能是某个点的环外子树直径
• 基环树直径可能是两个环点的最长链拼接，再加上环上距离

同样的，枚举环上某一条边，强制断边，变成一条单链后

可以用前缀和差分求环上两点的距离，距离有两种

• 恰好顺着断边的顺序
  • $su{m}_j-su{m}_i$
• 反着走环
  • $len-(su{m}_j-su{m}_i)$

则环上点拼接成直径的转移为

$\max (f_i+f_j+su{m}_j-su{m}_i,f_i+f_j+len-su{m}_j+su{m}_i)$

发现$i,j$之间是独立的，枚举到$j$时，记录前面最大贡献的$i$

Max1=max⁡{fi−sumi};Max2=max⁡{fi+sumi}Max_1=\max\{f_i-sum_i\};Max_2=\max\{f_i+sum_i\}Max1​=max{fi​−sumi​};Max2​=max{fi​+sumi​}

$\max (f_j+su{m}_j+Ma{x}_1,f_j+len-su{m}_j+Ma{x}_2)$

但是只有当环跑完后我们才知道环长$len$

所以可以把$len$提出去，最后加上再选较大值

#include <queue>
#include <cstdio>
#include <iostream>
using namespace std;
#define int long long
#define maxn 1000005
queue < int > q;
int to[maxn], d[maxn], w[maxn], f[maxn], g[maxn];
bool vis[maxn];
int n;int dfs( int now ) {int x = to[now], sum = w[now];int ans1 = g[now], Max1 = f[now];int ans2 = - 1e18, Max2 = f[now];while( x ^ now ) {d[x] = 0;ans1 = max( ans1, g[x] );ans1 = max( ans1, f[x] + sum + Max1 );ans2 = max( ans2, f[x] - sum + Max2 );Max1 = max( Max1, f[x] - sum );Max2 = max( Max2, f[x] + sum );sum += w[x];x = to[x];}return max( ans1, ans2 + sum );
}signed main() {scanf( "%lld", &n );	for( int i = 1;i <= n;i ++ )scanf( "%lld %lld", &to[i], &w[i] ), d[to[i]] ++;for( int i = 1;i <= n;i ++ )if( ! d[i] ) q.push( i );while( ! q.empty() ) {int u = q.front(); q.pop();int v = to[u];g[v] = max( g[v], max( g[u], f[v] + f[u] + w[u] ) );f[v] = max( f[v], f[u] + w[u] );d[v] --;if( ! d[v] ) q.push( v );}int ret = 0;for( int i = 1;i <= n;i ++ ) if( d[i] ) ret += dfs( i );printf( "%lld\n", ret );return 0;
}

[NOIP2018 提高组] 旅行 加强版

luogu5049

• m=n-1
  • 就是单纯的一棵树，直接dfs搜就可以了
• m=n
  • 基环树

一个点只能访问未访问点，或者选择回溯

考虑对于基环树环上点的几种选择

• case1

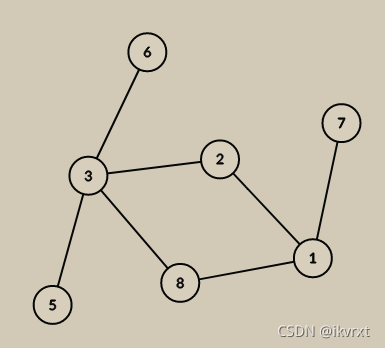
对于节点3，肯定是由2过来的，最佳选择是先遍历完非环的树的点5,6，再走环

是不会选择回溯到2的

• case2

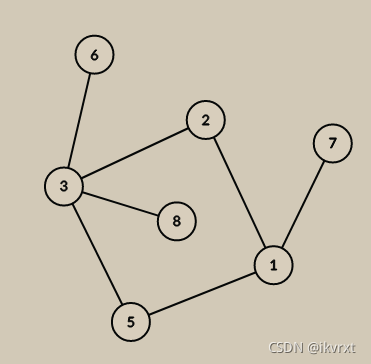
3的环边5是其所有边中最小的，优选走环，后遍历非环树，不选择回溯

• case3

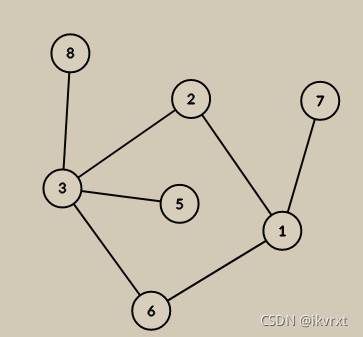
3的环边6不是最大也不是最小，选择先遍历5再走环边，最后遍历8，同样不会选择回溯

发现只有当环边是最大边的时候就会选择遍历完非环树后回溯

但真的这样就直接回溯了吗？

• case4

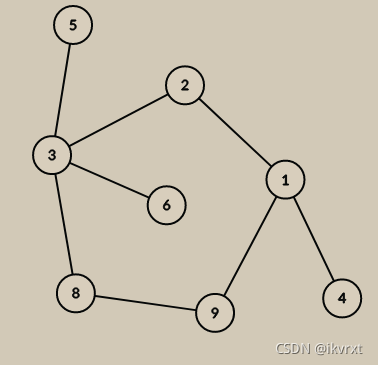
走到3的时候，遍历5,6，但是发现回溯后走的是9并没有比8小，也是应该不回溯的

综上，只有环边是最大边且比回溯后走的第一条边大的时候才会选择回溯

#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
#define maxn 500005
vector < int > ans;
struct node { int u, v; }edge[maxn << 1];
int head[maxn], to[maxn << 2], nxt[maxn << 2], f[maxn];
bool vis[maxn], circle[maxn];
bool flag1, flag2, flag3;
int n, m, cnt, Max;void dfs1( int u ) {vis[u] = 1;ans.push_back( u );for( int i = head[u];~ i;i = nxt[i] ) {int v = to[i];if( vis[v] ) continue;else dfs1( v );}
}void dfs2( int now, int fa ) {if( flag2 ) return;if( ! f[now] ) f[now] = fa;else {do {circle[fa] = 1;fa = f[fa];} while( fa ^ f[now] );flag2 = 1;return;}for( int i = head[now];~ i;i = nxt[i] )if( to[i] ^ fa ) dfs2( to[i], now );
}void dfs3( int u ) {vis[u] = 1;ans.push_back( u );if( circle[u] ) {bool flag = 0;for( int i = head[u];~ i;i = nxt[i] ) {if( flag3 ) break;if( ! circle[to[i]] or vis[to[i]] ) continue;int v = to[i];i = nxt[i];while( vis[to[i]] ) i = nxt[i];if( ~ i ) Max = to[i];else if( v > Max ) flag = flag3 = 1;break;}for( int i = head[u];~ i;i = nxt[i] ) if( vis[to[i]] or ( flag and circle[to[i]] ) ) continue;else dfs3( to[i] );}elsefor( int i = head[u];~ i;i = nxt[i] )if( vis[to[i]] ) continue;else dfs3( to[i] );
}int main() {scanf( "%d %d", &n, &m );if( m == n - 1 ) flag1 = 1;for( int i = 1, u, v;i <= m;i ++ ) {scanf( "%d %d", &u, &v );edge[i] = { u, v };edge[i + m] = { v, u };}m <<= 1;sort( edge + 1, edge + m + 1, []( node x, node y ) { return x.v > y.v; } );memset( head, -1, sizeof( head ) );for( int i = 1;i <= m;i ++ ) {int u = edge[i].u, v = edge[i].v;to[cnt] = v, nxt[cnt] = head[u], head[u] = cnt ++;}if( flag1 ) dfs1( 1 );else {dfs2( 1, 0 );Max = 1e9;dfs3( 1 );}for( auto i : ans ) printf( "%d ", i );return 0;
}

CF1454E Number of Simple Paths

CF1454E

非常简单

跑出环和非环树

• 两个点隶属于同一个环点的非环树（之间不会经过环）
  • 从子树大小中选两个数，$siz\ast (siz-1)/2$
• 经过环的两点之间的方案数有两种（走环的不同方向）
  • 从子树中选一个，在子树外选一个，$siz\ast (n-siz)/2\ast 2=siz\ast (n-siz)$

#include <cstdio>
#include <vector>
using namespace std;
#define int long long
#define maxn 200005
vector < int > G[maxn];
int T, n;
bool flag;
int f[maxn], siz[maxn];
bool circle[maxn];void dfs1( int u, int fa ) {if( flag ) return;if( ! f[u] ) f[u] = fa;else {do {circle[fa] = 1;fa = f[fa];} while( f[u] ^ fa );flag = 1;return;}for( auto v : G[u] ) if( v ^ fa ) dfs1( v, u );
}void dfs2( int u, int fa ) {siz[u] = 1;for( auto v : G[u] ) {if( v == fa or circle[v] ) continue;else dfs2( v, u ), siz[u] += siz[v];}
}signed main() {scanf( "%lld", &T );while( T -- ) {scanf( "%lld", &n );flag = 0;for( int i = 1;i <= n;i ++ ) circle[i] = f[i] = 0, G[i].clear();for( int i = 1, u, v;i <= n;i ++ ) {scanf( "%lld %lld", &u, &v );G[u].push_back( v );G[v].push_back( u );}dfs1( 1, 0 );int ans = 0;for( int i = 1;i <= n;i ++ )if( circle[i] ) {dfs2( i, 0 );ans += siz[i] * ( siz[i] - 1 ) / 2 + siz[i] * ( n - siz[i] );}printf( "%lld\n", ans );}return 0;
}

Traffic Network in Numazu

HDU6393

同样的，断环为链

两点间的距离分为三种

• 两点在同一棵非环树内，直接求出两个点的lca，再计算
• 经过环
  • 两点到环的两端，然后加上断的边长
  • 两点到环的相反两端，然后加上断的边长

利用线段树可以维护，但是树状数组更好写

断树后进行dfn序的重置，修改一条边其实是对于一个连续区间的修改

#include <cstdio>
#include <vector>
#include <iostream>
using namespace std;
#define int long long
#define maxn 100005
struct node { int u, v, w; }E[maxn];
vector < node > G[maxn];
int Ti, n, Q, cnt, S, T, id, len;
int L[maxn], R[maxn], t[maxn], f[maxn], dep[maxn];
int p[maxn][20];int lowbit( int i ) { return i & -i; }void modify( int i, int val ) {for( ;i <= n;i += lowbit( i ) ) 	t[i] += val;
}int query( int i ) {int ans = 0;for( ;i;i -= lowbit( i ) )ans += t[i];return ans;
}int find( int x ) { return x == f[x] ? x : f[x] = find( f[x] ); }void dfs( int u, int fa, int w ) {dep[u] = dep[fa] + 1;p[u][0] = fa;for( int i = 1;i < 20;i ++ )p[u][i] = p[p[u][i - 1]][i - 1];L[u] = ++ cnt;modify( L[u], w );for( auto i : G[u] )if( i.v ^ fa ) dfs( i.v, u, i.w );R[u] = cnt;modify( R[u] + 1, -w );
}int lca( int u, int v ) {if( dep[u] < dep[v] ) swap( u, v );for( int i = 19;~ i;i -- )if( dep[p[u][i]] >= dep[v] )u = p[u][i];if( u == v ) return u;for( int i = 19;~ i;i -- )if( p[u][i] ^ p[v][i] )u = p[u][i], v = p[v][i];return p[u][0];
}int dis( int x, int y ) {return query( L[x] ) + query( L[y] ) - query( L[lca( x, y )] ) * 2;
}signed main() {scanf( "%lld", &Ti );while( Ti -- ) {scanf( "%lld %lld", &n, &Q );cnt = 0;for( int i = 1;i <= n;i ++ ) {G[i].clear();f[i] = i;t[i] = 0;for( int j = 0;j < 20;j ++ )p[i][j] = 0;}for( int i = 1, u, v, w;i <= n;i ++ ) {scanf( "%lld %lld %lld", &u, &v, &w );if( find( u ) == find( v ) )S = u, T = v, id = i, len = w;else {G[u].push_back( { u, v, w } );G[v].push_back( { v, u, w } );E[i] = { u, v, w };f[find( v )] = find( u );}}dfs( 1, 0, 0 );	for( int i = 1, opt, x, y;i <= Q;i ++ ) {scanf( "%lld %lld %lld", &opt, &x, &y );if( ! opt ) if( x == id ) len = y;else {int now = p[E[x].u][0] == E[x].v ? E[x].u : E[x].v;modify( L[now], y - E[x].w );modify( R[now] + 1, E[x].w - y );E[x].w = y;}else printf( "%lld\n", min( dis( x, y ), min( dis( x, S ) + dis( y, T ), dis( x, T ) + dis( y, S ) ) + len ) );}}return 0;
}

Card Game

HDU6403

---

一张牌的两面，要求朝上面的数字互不相同

显然是将牌的两面连边，一条边也就代表一张牌，数字互不相同就是选择不同的点

• 对于“树”的方案
  • 钦定其中某个点不选，则剩下的点都被钦定，方案数为树的大小
• 对于“环”的方案
  • 只有两种方案（均选左和均选右）

这是很基础的“牌的两面”基环树应用的处理方法

---

转回此题，题目可以翻译为

将牌的反面向正面连边，求反转最少边数的方案数，使得每个点的入度不超过1

显然当且仅当图为树或基环树的时候才有解

且此题很有可能有重边和自环

同样的将环拆成链后再单独考虑被强断的那条边的贡献

对于树就单纯的树形$DP$做

具体而言

• 求出每个连通块的点数和边数

• 若边数不是点数或者点数减一，就无解

• 若边数等于点数，说明是个基环树

  • 断开一条边后以边的两端开始遍历一遍分别求出最少反转的边数

    （边数跟连边的边权有关，下面有阐释）

  • 如果加上这条边的贡献相同方案数为2，否则为1

• 若边数等于点数减一，说明是个普通的树

  • 树形$DP$，求出以每个点为根（钦定不选）的最少反转次数

  • 其实最少反转数在换根$DP$父亲向儿子转移的时候才会发生变化，且变化只有$1$

    如何根据边权推测变化+1或者-1

    • 对于一张牌，正面向反面建边权为1，反面向正面建边权为0
    • $u$不选时的答案为$d{p}_u$，转移到儿子$v$不选时
    • 如果$u\to v$的边权为1，说明一张牌本来是$u$在上，$d{p}_u$为了不选$u$将其反转了
    • 那么变成不选$v$时，就需要选择$u$，这张牌就变成了不反转，操作次数就减一
    • 所以$d{p}_v=d{p}_u-1$
    • 反之自然是$d{p}_v=d{p}_u+1$

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define int long long
#define mod 998244353
#define maxn 200005
int Case, n, node, edge, cnt, S, T, id, top;
int head[maxn], to[maxn], nxt[maxn], w[maxn], f[maxn], g[maxn], dp[maxn];
bool vis[maxn];void dfs1( int now ) {vis[now] = 1;node ++;for( int i = head[now];~ i;i = nxt[i] ) {edge ++;if( ! vis[to[i]] ) dfs1( to[i] );}
}void dfs2( int now, int ID ) {vis[now] = 1;f[now] = 0;for( int i = head[now];~ i;i = nxt[i] ) {if( i == ID ) continue;if( ! vis[to[i]] ) {dfs2( to[i], i ^ 1 );f[now] += f[to[i]] + w[i];}else S = now, T = to[i], id = i;}
}void dfs3( int now, int ID ) {dp[++ top] = g[now];for( int i = head[now];~ i;i = nxt[i] )if( i == ID or i == ( id ^ 1 ) or i == id ) continue;else {g[to[i]] = g[now] + ( w[i] ? -1 : 1 );dfs3( to[i], i ^ 1 );}
}signed main() {scanf( "%lld", &Case );nxt :while( Case -- ) {scanf( "%lld", &n );memset( head, -1, sizeof( head ) );memset( vis, 0, sizeof( vis ) );cnt = 0;for( int i = 1, x, y;i <= n;i ++ ) {scanf( "%lld %lld", &x, &y );w[cnt] = 1, to[cnt] = y, nxt[cnt] = head[x], head[x] = cnt ++;w[cnt] = 0, to[cnt] = x, nxt[cnt] = head[y], head[y] = cnt ++;}for( int i = 1;i <= n;i ++ )if( ! vis[i] ) {node = edge = 0;dfs1( i );edge >>= 1;if( edge > node ) {printf( "-1 -1\n" );goto nxt;}}memset( vis, 0, sizeof( vis ) );int ret = 0, ans = 1; n <<= 1;for( int i = 1;i <= n;i ++ )if( ! vis[i] ) {S = T = cnt = top = 0, id = -1;dfs2( i, -1 );g[i] = f[i];dfs3( i, -1 );if( ! S ) {sort( dp + 1, dp + top + 1 );for( int j = 1;j <= top;j ++ )if( dp[j] == dp[1] ) cnt ++;else break;ret += dp[1];}else {id &= 1;if( g[S] + id == g[T] + ( id ^ 1 ) ) cnt = 2;else cnt = 1;ret += min( g[S] + id, g[T] + ( id ^ 1 ) );}ans = ans * cnt % mod;}printf( "%lld %lld\n", ret, ans );}return 0;
}