线段树合并与 fhq-treap合并很类似，也是将两个不同根的线段树暴力合并

至于时间复杂度，线段树合并一次是可以达到$O(n)$的，但是大家都是算平摊复杂度的，平摊后就是$\log$级别了

int merge( int x, int y, int l, int r ) {if( ! x or ! y ) return x + y;if( l == r ) { //操作一下return x;}int mid = ( l + r ) >> 1;t[x].l = merge( t[x].l, t[y].l, l, mid );t[x].r = merge( t[x].r, t[y].r, mid + 1, r );//再合并操作一下return x;
}

如果是树的线段树合并

就是先操作完儿子，再插入父亲

void dfs( int u, int fa ) {for( auto v : G[u] ) {if( v == fa ) continue;else dfs( v, u );root[u] = merge( root[u], root[v], 1, n );}//可能还有点操作modify( root[u], 1, n, [] );
}

[HNOI2012]永无乡

BZOJ2733

初始每个岛屿自己是一个连通块，自己单开一个权值线段树（使用动态开点）

然后就很暴力，利用并查集可以判断那两个岛屿是否已经在一个连通块

不在就直接线段树合并，在就不管

查询就找到其所在连通块的线段树，直接查就是了

#include <cstdio>
#define maxn 100005
struct node { int l, r, id, tot; }t[maxn * 50];
int f[maxn], root[maxn];
int n, m, cnt;int find( int x ) { return x == f[x] ? x : f[x] = find( f[x] ); }void modify( int &now, int l, int r, int pos, int id ) {if( ! now ) now = ++ cnt;if( l == r ) { t[now].id = id, t[now].tot ++; return; }int mid = ( l + r ) >> 1;if( pos <= mid ) modify( t[now].l, l, mid, pos, id );else modify( t[now].r, mid + 1, r, pos, id );t[now].tot = t[t[now].l].tot + t[t[now].r].tot;
}int merge( int x, int y, int l, int r ) {if( ! x or ! y ) return x + y;if( l == r ) { if( t[y].id ) t[x].id = t[y].id;t[x].tot += t[y].tot;return x;}int mid = ( l + r ) >> 1;t[x].l = merge( t[x].l, t[y].l, l, mid );t[x].r = merge( t[x].r, t[y].r, mid + 1, r );t[x].tot = t[t[x].l].tot + t[t[x].r].tot;return x;
}int query( int now, int k, int l, int r ) {if( ! now or t[now].tot < k ) return -1;int mid = ( l + r ) >> 1;if( l == r ) return t[now].id;if( t[t[now].l].tot >= k ) return query( t[now].l, k, l, mid );else return query( t[now].r, k - t[t[now].l].tot, mid + 1, r );
}int main() {scanf( "%d %d", &n, &m );for( int i = 1, x;i <= n;i ++ ) {scanf( "%d", &x );modify( root[i], 1, n, x, i );f[i] = i;}for( int i = 1, u, v;i <= m;i ++ ) {scanf( "%d %d", &u, &v );u = find( u );v = find( v );f[v] = u;root[u] = merge( root[u], root[v], 1, n );}char opt[10]; int x, y, Q;scanf( "%d", &Q );while( Q -- ) {scanf( "%s %d %d", opt, &x, &y );if( opt[0] == 'B' ) {x = find( x );y = find( y );if( x == y ) continue;else f[y] = x, root[x] = merge( root[x], root[y], 1, n );}else {x = find( x );printf( "%d\n", query( root[x], y, 1, n ) );}}return 0;
}

Lomsat gelral

CF600E

dfs先操作儿子，儿子操作完后并到父亲线段树内

线段树维护区间颜色出现最大值，和颜色编号和，基操

#include <cstdio>
#include <vector>
using namespace std;
#define maxn 100005
#define int long long
vector < int > G[maxn];
struct node { int l, r, Max, sum; }t[maxn * 50];
int cnt, n;
int c[maxn], root[maxn];void pushup( int now ) {if( t[t[now].l].Max > t[t[now].r].Max ) {t[now].Max = t[t[now].l].Max;t[now].sum = t[t[now].l].sum;}else if( t[t[now].l].Max < t[t[now].r].Max ) {t[now].Max = t[t[now].r].Max;t[now].sum = t[t[now].r].sum;}else {t[now].Max = t[t[now].l].Max;t[now].sum = t[t[now].l].sum + t[t[now].r].sum;}
}void modify( int &now, int l, int r, int pos ) {if( ! now ) now = ++ cnt;if( l == r ) { t[now].Max ++, t[now].sum = l; return; }int mid = l + r >> 1;if( pos <= mid ) modify( t[now].l, l, mid, pos );else modify( t[now].r, mid + 1, r, pos );pushup( now );
}int merge( int now, int lst, int l, int r ) {if( ! now or ! lst ) return now + lst;if( l == r ) { t[now].Max += t[lst].Max; return now; }int mid = l + r >> 1;t[now].l = merge( t[now].l, t[lst].l, l, mid );t[now].r = merge( t[now].r, t[lst].r, mid + 1, r );pushup( now );return now;
}void dfs( int u, int fa ) {for( auto v : G[u] ) {if( v == fa ) continue;else dfs( v, u );root[u] = merge( root[u], root[v], 1, n );}modify( root[u], 1, n, c[u] );
}signed main() {scanf( "%lld", &n );for( int i = 1;i <= n;i ++ ) {scanf( "%lld", &c[i] );root[i] = i;cnt ++;}for( int i = 1, u, v;i < n;i ++ ) {scanf( "%lld %lld", &u, &v );G[u].push_back( v );G[v].push_back( u );  }dfs( 1, 0 );for( int i = 1;i <= n;i ++ )printf( "%lld ", t[root[i]].sum );return 0;
}

「POI2011 R2 Day2」旋转树木 Tree Rotations

LOJ2163

性质：考虑相同长度的不交的两段$x,y$要计算逆序对，则$x$再分成相同长度不交的两段$a,b$

不管是$a,b$还是$b,a$，$x$与$y$的逆序对（一个来自$x$，一个来自$y$）数量不会变

因为换不换，都是在$y$前面

这就可以用线段树维护，这个性质意味着儿子换不换，对父亲与其他父亲间的计算没有影响

所以建立权值线段树，直接对于每一层线段树合并

先计算左右儿子不换，和换的逆序对，再合并

合并完后，选择更小的方案

#include <cstdio>
#include <iostream>
using namespace std;
#define maxn 200005
#define int long long
struct node { int l, r, ans; }t[maxn * 50];
int cnt, nxd1, nxd2;void modify( int &now, int l, int r, int pos ) {if( ! now ) now = ++ cnt;t[now].ans ++;if( l == r ) return;int mid = l + r >> 1;if( pos <= mid ) modify( t[now].l, l, mid, pos );else modify( t[now].r, mid + 1, r, pos );
}int merge( int x, int y, int l, int r ) {if( ! x or ! y ) return x + y;t[x].ans += t[y].ans;if( l == r ) return x;int mid = l + r >> 1;nxd1 += t[t[x].r].ans * t[t[y].l].ans;nxd2 += t[t[x].l].ans * t[t[y].r].ans;t[x].l = merge( t[x].l, t[y].l, l, mid );t[x].r = merge( t[x].r, t[y].r, mid + 1, r );return x;
}int n, x, ans, node;
int root[maxn];
void dfs( int &k ) {scanf( "%lld", &x );if( x ) {k = ++ node;modify( root[k], 1, n, x );return;}int l, r;dfs( l );dfs( r );nxd1 = 0;nxd2 = 0;merge( root[l], root[r], 1, n );ans += min( nxd1, nxd2 );k = l;
}signed main() {scanf( "%lld", &n );dfs( n );printf( "%lld\n", ans );return 0;
}

Escape Through Leaf

CF932F

首先，有个简单的$n^2$的$dp$：设$d{p}_u:u$的答案，则dpu=min⁡{dpv+av∗bu}v∈sonudp_u=\min\{dp_v+a_v*b_u\}\quad v\in son_udpu​=min{dpv​+av​∗bu​}v∈sonu​

这完完全全就是李超线段树的长相

直接dfs树合并李超线段树

考虑两条直线的合并，t[x]表示原先已有的直线，now表示这一次新加的直线

• 新直线的斜率更大，判断在mid处两条直线的值大小

  • 新直线更小

    

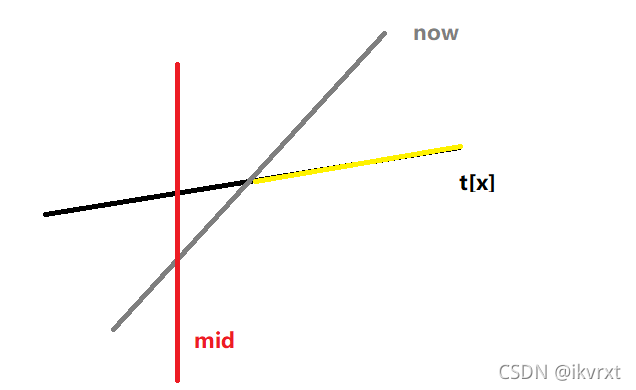
    原直线可能在mid右边有贡献，继续修改右儿子，并且mid处的直线被更新成新直线

  • 新直线更大

    

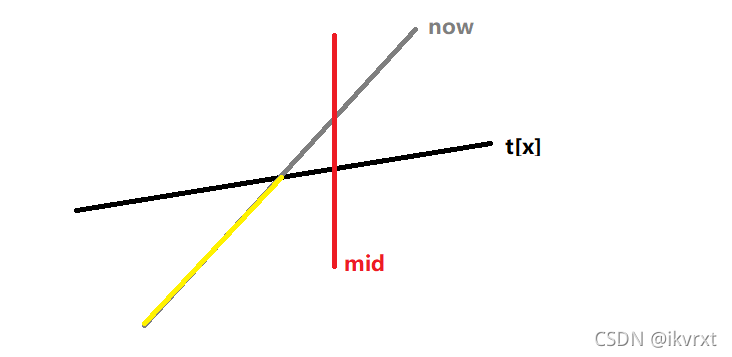
    新直线可能在mid左边有贡献，继续修改左儿子，并且mid处的直线不会被更新

• 新直线的斜率更小，判断在mid处两条直线的值大小

  • 新直线更小

    

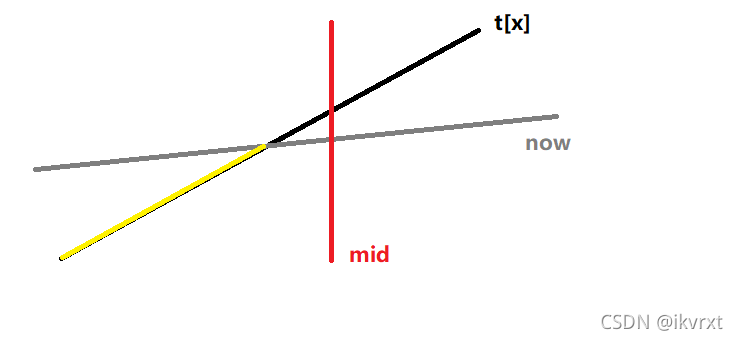
    原直线可能在mid左边有贡献，继续修改左儿子，并且mid处的直线被更新成新直线

  • 新直线更大

    

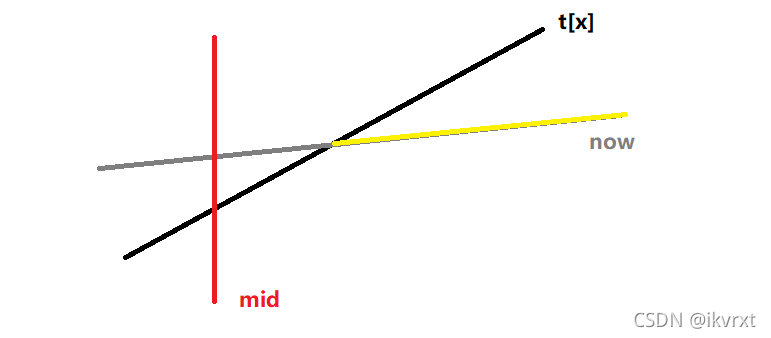
    新直线可能在mid右边有贡献，继续修改右儿子，并且mid处的直线不会被更新

• 斜率相同

  

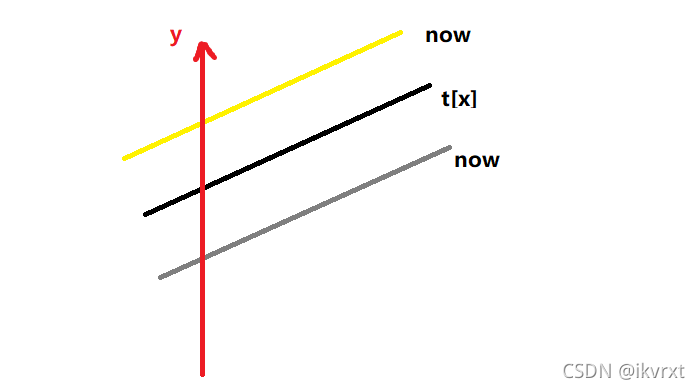
  直接判断截距的大小，选择截距小的直线，直接覆盖完

#include <cstdio>
#include <vector>
#include <iostream>
using namespace std;
#define maxn 100005
#define int long long
vector < int > G[maxn];
struct node { int k, b; }t[maxn * 50];
int a[maxn], b[maxn], root[maxn], ans[maxn], lson[maxn * 50], rson[maxn * 50];
int n, cnt;int calc( node l, int x ) { return l.k * x + l.b; }void modify( int &x, int l, int r, node now ) {if( ! x ) { t[x = ++ cnt] = now; return; }if( l == r ) { t[x] = calc( t[x], l ) < calc( now, l ) ? t[x] : now; return; }int mid = ( l + r ) >> 1;if( now.k > t[x].k ) {if( calc( now, mid ) <= calc( t[x], mid ) ) modify( rson[x], mid + 1, r, t[x] ), t[x] = now;else modify( lson[x], l, mid, now );}else if( now.k < t[x].k ) {if( calc( now, mid ) <= calc( t[x], mid ) )modify( lson[x], l, mid, t[x] ), t[x] = now;elsemodify( rson[x], mid + 1, r, now );}else if( now.b < t[x].b ) t[x] = now;
}int query( int now, int l, int r, int x ) {if( ! now ) return 1e18;if( l == r ) return calc( t[now], x );int mid = ( l + r ) >> 1, ret;if( x <= mid ) ret = query( lson[now], l, mid, x );else ret = query( rson[now], mid + 1, r, x );return min( ret, calc( t[now], x ) );
}int merge( int x, int y, int l, int r ) {if( ! x or ! y ) return x + y;if( l == r ) { return calc( t[x], l ) < calc( t[y], l ) ? x : y; }int mid = ( l + r ) >> 1;lson[x] = merge( lson[x], lson[y], l, mid );rson[x] = merge( rson[x], rson[y], mid + 1, r );modify( x, l, r, t[y] );return x;
}void dfs( int u, int fa ) {bool flag = 0;for( auto v : G[u] ) {if( v == fa ) continue;else dfs( v, u );flag = 1;root[u] = merge( root[u], root[v], -1e5, 1e5 );}node line;line.k = b[u];if( flag ) ans[u] = line.b = query( root[u], -1e5, 1e5, a[u] );else ans[u] = line.b = 0;modify( root[u], -1e5, 1e5, line );
}signed main() {scanf( "%lld", &n );for( int i = 1;i <= n;i ++ ) scanf( "%lld", &a[i] );for( int i = 1;i <= n;i ++ ) scanf( "%lld", &b[i] );for( int i = 1, u, v;i < n;i ++ ) {scanf( "%lld %lld", &u, &v );G[u].push_back( v );G[v].push_back( u ); }dfs( 1, -1 );for( int i = 1;i <= n;i ++ ) printf( "%lld ", ans[i] );return 0;
}