解析

纯纯的人类智慧题。

关键性质：$v$ 可以在计算 $f(u,G)$ 时产生贡献，当且仅当 $G$ 中 $u,v$ 之间可以通过 $[v,n]$ 的点互相到达。
充分性较为显然，编号更大的点不会比 $v$ 先删去，所以必然在 $v$ 时刻依然存在。
必要性证明：假设 $v$ 时刻 $u\to v$ 的路径上存在一个 $x\in [1,v)$，在 $x$ 时刻图的联通性不弱于 $v$ 时刻，因而必然也有 $u\to x$ 可达，且由于 $x\to v,v\to u$ 皆可达，也就有 $x\to u$ 可达，$x$ 应当被删去，矛盾。

接下来的任务就是如何维护这个东西。

floyd

对于点编号属于 $[v,n]$ 这样的限制，不难想到 floyd。但是直接跑无法通过 $n=1000$。
然后拿大样例试了试，发现写成：

for(int k=n;k>=1;k--){for(int i=1;i<=k;i++){for(int j=i;j<=n;j++){k -> update(i,j)}}}

答案依然是对的，并且能跑过1000了。
然后就完事了。

我们当然要想一想为什么这样是对的。
这么转移必然出问题的就是两边的点编号均大于 $k$ 的情况。
如图中的 $p,q$：
（高度表示点编号的相对大小）

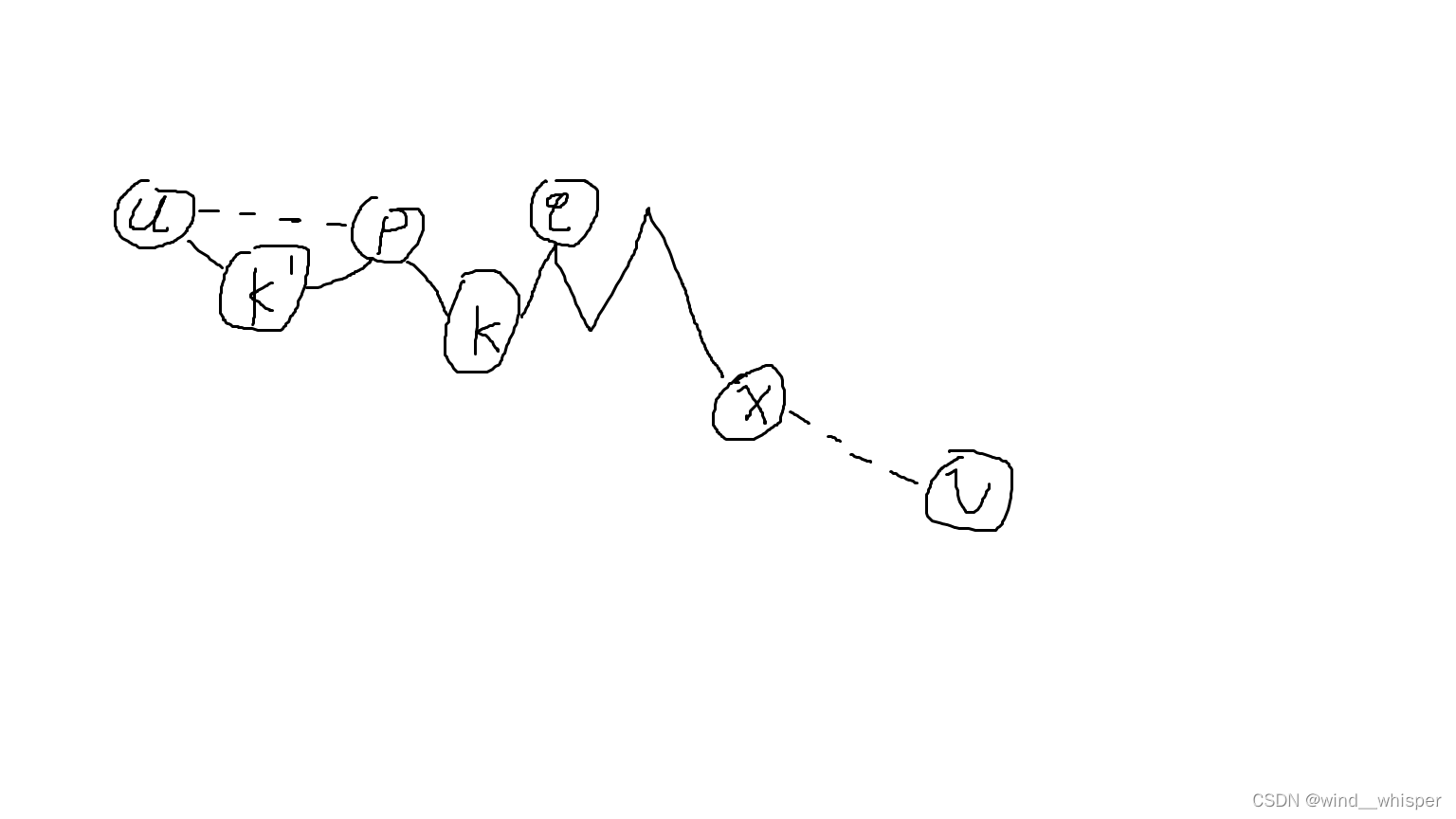
那么我们现在就要证明：

若 $(x,y)$ 路径上没有经过 $[1,\min (x,y))$ 的点，就必然可以正确转移。

假设枚举到中转点 $k$ 之前的路径都符合这个性质。
对于当前枚举的中转点 $k$，注意到我们需要求出的合法路径必然至少有一个端点是小于 $k$ 的。
那么就必然能在 $k$ 的某一侧找到第一个编号小于 $k$ 的点 $x$，$k\to x$ 这段路径使用 $(k,n]$ 的点中转，不会出现现在 $p,q$ 这样的窘境，所以 $f(k,x)$ 当前是对的。
那么 $x$ 就可以通过 $k$ 连接起另一侧的 $p$ ，得到正确的 $f(p,x)$。
如果 $(u,p)$ 之间有 $k^{\prime }$ 这样的点导致 $f(u,p)$ 不对怎么办？把$(u,p)$ 最小的点 $k^{\prime }$ 当成 $p$ 的角色来考虑，刚才的证明就还是对的。

bfs

本题看题解，还有通过 bfs 求对每个 $v$ 考虑在每张图中能对多少 $u$ 产生贡献的方法来做的，每次 bfs 用到一条边就直接删去，从而保证复杂度为 $O(nm)$，也挺妙的。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define debug(...) fprintf(stderr,__VA_ARGS__)
#define ok debug("OK\n")
using namespace std;const int N=1050;
const int M=2e5+100;
const int inf=1e9;
const int mod=19921228;inline ll read(){ll x(0),f(1);char c=getchar();while(!isdigit(c)) {if(c=='-')f=-1;c=getchar();}while(isdigit(c)) {x=(x<<1)+(x<<3)+c-'0';c=getchar();}return x*f;
}int n,m;
int f[N][N];
ll sum[M];signed main() {
#ifndef ONLINE_JUDGEfreopen("a.in","r",stdin);freopen("a.out","w",stdout);
#endif//memset(f,0x3f,sizeof(f));n=read();m=read();for(int i=1;i<=m;i++){int x=read(),y=read();f[x][y]=i;}for(int i=1;i<=n;i++) f[i][i]=m+1;for(int k=n;k>=1;k--){for(int i=k;i<=n;i++) sum[min(f[i][k],f[k][i])]++;for(int i=1;i<=k;i++){//if(!f[i][k]&&!f[k][i]) continue;for(int j=i;j<=n;j++){f[i][j]=max(f[i][j],min(f[i][k],f[k][j]));f[j][i]=max(f[j][i],min(f[j][k],f[k][i]));}}}for(int i=m;i>=1;i--) sum[i]+=sum[i+1];for(int i=1;i<=m+1;i++) printf("%lld ",sum[i]);return 0;
}
/*
*/