CF765F Souvenirs
- problem
- solution
- code
problem
题目链接
solution
这个势能线段树简直是太巧妙了!!!( ఠൠఠ )ノ
将询问按右端点升序离线下来。
对于每一个右端点 rrr,维护 ansi=min{∣ai−aj∣,j∈[i,r]}ans_i=\min\{|a_i-a_j|,j\in[i,r]\}ansi=min{∣ai−aj∣,j∈[i,r]}。
用线段树查询区间 [l,r][l,r][l,r] 内的 min{ansi,i∈[l,r]}\min\{ans_i,i\in[l,r]\}min{ansi,i∈[l,r]} 就是答案了。
时间复杂度的瓶颈在于修改维护线段树上面。暴力做是 O(n2)O(n^2)O(n2) 的。
考虑优化。假设 ansians_iansi 的最优选择点在 jjj。
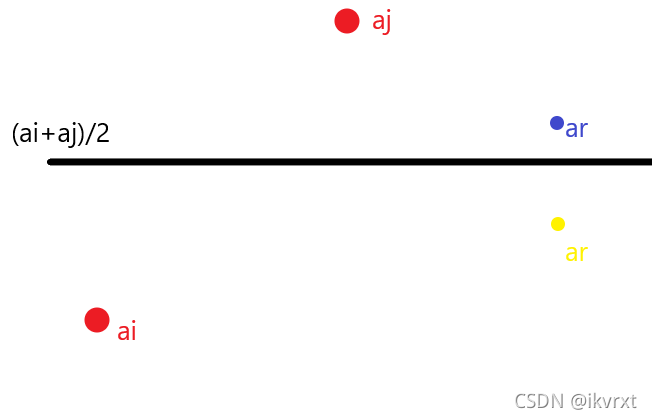
-
如果 ara_rar 是在黄色点,即 <ai+aj2<\frac{a_i+a_j}{2}<2ai+aj ,这个时候要必须更新 ansians_iansi。这会让 ansians_iansi 的值变小至少一半。
-
如果 ara_rar 是在蓝色点,即 >ai+aj2>\frac{a_i+a_j}{2}>2ai+aj,这个时候直接更新 ansjans_jansj 而不再更新 ansians_iansi。
因为 j>i∧ansj<ansij>i\wedge ans_j<ans_ij>i∧ansj<ansi ,最后 rrr 的询问肯定答案是不会选到 ansians_iansi 的。
所以就算 ansians_iansi 是错的,也不影响!
-
如果 ara_rar 在 aia_iai 等值线下面,也是一样的。
将 ansians_iansi 看作势能,递减到 000 时就不再更新。每次更新至少减少一半。
所以修改点数应该是 nlogan\log anloga 的。
具体而言:先修改右区间,再修改左区间。且如果当前修改的答案不如之前更新的答案,就直接跳过即可。同时需要存储下区间内所有的 aaa。
这样实际操作的只有必须更新的点。
总时间复杂度为:O(nlognloga)O(n\log n\log a)O(nlognloga)
code
#include <vector>
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
#define maxn 400005
#define inf 0x7f7f7f7f
vector < int > G[maxn];
struct node { int l, r, id; }q[maxn];
int n, Q;
int a[maxn], ans[maxn];namespace SegMentTree {int ans = inf;int Min[maxn];#define lson now << 1#define rson now << 1 | 1void build( int now, int l, int r ) {Min[now] = inf;for( int i = l;i <= r;i ++ ) G[now].push_back( a[i] );sort( G[now].begin(), G[now].end() );if( l == r ) return;int mid = ( l + r ) >> 1;build( lson, l, mid );build( rson, mid + 1, r );}/*void modify( int now, int l, int r, int R, int x ) {if( R < l ) return;if( r <= R ) {auto it = lower_bound( G[now].begin(), G[now].end(), x );if( it != G[now].end() ) Min[now] = min( Min[now], (*it) - x );if( it != G[now].begin() ) Min[now] = min( Min[now], x - *(it - 1) );if( Min[now] >= ans ) return;}if( l == r ) { ans = min( ans, Min[now] ); return; }int mid = ( l + r ) >> 1;modify( rson, mid + 1, r, R, x ); //优先更新最近的点modify( lson, l, mid, R, x );Min[now] = min( Min[lson], Min[rson] );ans = min( ans, Min[now] );}*/void modify( int now, int l, int r, int R, int x ) {if( R < l ) return;if( r <= R ) {it = lower_bound( G[now].begin(), G[now].end(), x );int tmp = inf;if( it != G[now].end() ) tmp = *it - x;if( it != G[now].begin() ) it--, tmp = min( tmp, x - *it );Min[now] = min( Min[now], tmp );if( tmp >= ans ) return;}if( l == r ) { ans = min( ans, Min[now] ); return; }modify( rson, mid + 1, r, R, x );ans = min( ans, Min[rson] );modify( lson, l, mid, R, x );Min[now] = min( Min[lson], Min[rson] );ans = min( ans, Min[now] );}int query( int now, int l, int r, int L ) {if( r < L ) return inf;if( L <= l ) return Min[now];int mid = ( l + r ) >> 1;return min( query( lson, l, mid, L ), query( rson, mid + 1, r, L ) );}}int main() {scanf( "%d", &n );for( int i = 1;i <= n;i ++ ) scanf( "%d", &a[i] );scanf( "%d", &Q );for( int i = 1;i <= Q;i ++ ) scanf( "%d %d", &q[i].l, &q[i].r ), q[i].id = i;SegMentTree :: build( 1, 1, n );sort( q + 1, q + Q + 1, []( node x, node y ) { return x.r < y.r; } );int ip = 1;while( q[ip].r <= 1 ) ip ++;for( int i = 2;i <= n;i ++ ) {SegMentTree :: ans = inf;SegMentTree :: modify( 1, 1, n, i - 1, a[i] );while( q[ip].r == i )ans[q[ip].id] = SegMentTree :: query( 1, 1, n, q[ip].l ), ip ++;}for( int i = 1;i <= Q;i ++ ) printf( "%d\n", ans[i] );return 0;
}Upd:感谢评论区的 hack\text{hack}hack 数据让我发现自己的代码写得有点问题。
和小同志研究了一天发现是代码注释部分的问题。
大概就是,当前 iii 插入时,按照分析应该是遇到更优秀 jjj 就不再往左子树找了。
这个更优秀是和以前存的答案比较。
但是之前代码实现是和现在被覆盖的答案比较。势能就差得离谱。
现在新代码在叶子节点时输出访问次数就大概是 111。
但是。。。呃呃呃呃,现在这份代码加上读优跑评论区的数据最快也要 5s5s5s。。。
我们讨论了一下我这份代码的写法,更偏向 nlogn2logVn\log n^2\log Vnlogn2logV 的时间复杂度,因为要走 logn\log nlogn 层线段树,每层内还有个 vector\text{vector}vector 的二分。
可能把二分写在外面能少个 log\text{log}log 的嵌套。
但是跑评论区的数据每个点都只被访问了一次,时间复杂度我就不是很懂了?。
)


)
![P5303 [GXOI/GZOI2019]逼死强迫症(斐波拉契、矩阵乘法)](http://pic.xiahunao.cn/P5303 [GXOI/GZOI2019]逼死强迫症(斐波拉契、矩阵乘法))

![[2021 CSP-S提高组] 题解(廊桥分配+括号序列+回文+交通规划)](http://pic.xiahunao.cn/[2021 CSP-S提高组] 题解(廊桥分配+括号序列+回文+交通规划))

)
)


)

)

)

)
