又一最大子段和(牛客小白月赛38 )
题意:
我们将一个数列{an}的最大字段和的值记为S(a),现在你可以对进行若干次操作,每次操作,你可以选择数列中的一个数字,将其改为[−10100,10100][-10^{100},10^{100}][−10100,10100]之间的任意一个数。现在,给定整数x,求最少操作多少次可以使得S(a)=x
最大子段和是指选出数列中连续且非空的一段使得这段的和最大。
题解:
若S(a)=x,操作次数就是0
若S(a)<x,操作次数就是1,因为我们可以让最大子段和中的某一个元素加上(x-s(a))
若S(a)>x是最难想的,我们先想另一个问题:最少改多少个元素可以让S(a)<x?如果按照贪心的做法,当算上当前位第i位之后>x时,我们就要把第i位给改成负无穷(−10100-10^{100}−10100),这样就可以使得S(a)一定小于x,这样的操作次数记为ans1,现在每段都是小于x的,就变成了第二个情况,我们再操作一次就可以等于x,拿答案就是ans1+1。但实际上,这个1是可以省略的。
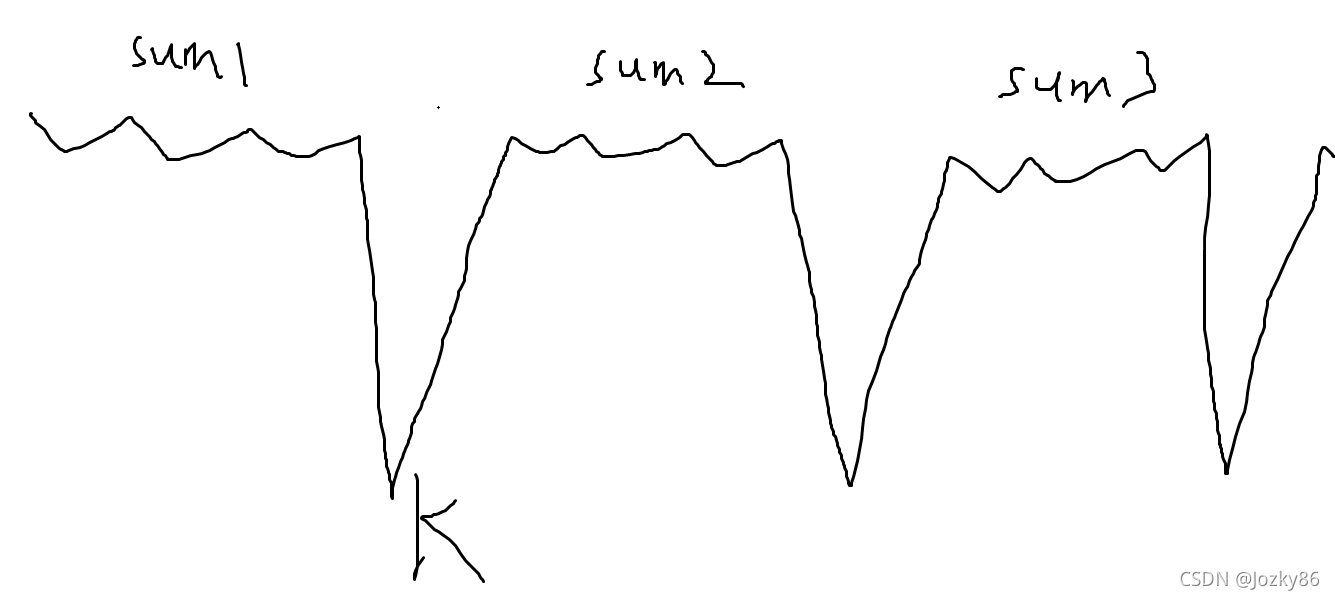
我们通过ans1次操作,将ans1个数改成极小值,这样相当于隔开好几份,每份sumisum_{i}sumi都小于x,那我们可以将两个相邻的sum1和sum2合并起来,让他们等于x,这可以通过k值来实现,我们让k取x-(sum1+sum2),这样sum1+k+sum2不就等于k了,其他ans1-1个位置依旧取负无穷
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N = 400010;
int main()
{ int _;cin>>_;while(_--){int n,x;cin>>n>>x;vector<ll>dp(n+1,0);ll maxv=-1e18;int cnt=0;for(int i=1;i<=n;i++){int xx;cin>>xx;dp[i]=xx;if(dp[i-1]>0) dp[i]+=dp[i-1];maxv=max(maxv,dp[i]);if(dp[i]>x){dp[i]-=1e18;cnt++;}}if(maxv==x) cout<<0<<endl;else if(maxv>x) cout<<cnt<<endl;else cout<<1<<endl;} return 0;}
/**
* In every life we have some trouble
* When you worry you make it double
* Don't worry,be happy.
**/




)
)





)


)
)


)