Surging 自2017年6月16日开源以来,已收到不少公司的关注或者使用,其中既有以海克斯康超大型等外企的关注,也不乏深圳泓达康、重庆金翅膀等传统行业的正式使用,自2019年年初,surging2.0 便已正式进入研发阶段,也受到了surging 用户的关注,本文将为您解读2.0的新特性和新功能。在开始之前先解答一下经常被提到的疑问
1.Surging 有没有文档、Demo、官网
因为需要完善Surging,暂时个人还没有时间去写文档,准备官网,但是大家可以通过关注liuhll,因为他正在写surging文档和 基于surging 的案例,
liuhll 文档:https://liuhll.github.io/hexo-blog-deploy/categories/%E5%BE%AE%E6%9C%8D%E5%8A%A1/
surging案例:https://github.com/liuhll/Surging.Sample
2. Surging 有没有公司正在使用
因为Surging 是开源产品,无法统计哪家公司正在使用,所以我提交了《surging 谁在使用》的issues, 大家可以去查看issues来知晓哪家公司正在使用,也请使用了surging的公司留下你所在公司的联系方式,以便收集有意向在生产上使用surging的客户,从而让surging社区和donetcore生态变得更加繁荣。
3. 何时支持Stage组件
对于Surging现在有一套独立的 surging 网关,而网关的设计违反了引擎组件化思想, 所以新的版本会基于KestrelHttpServer 组件扩展Stage,这样就能以组件模块化生成,以代替之前网关无法做到的缓存服务降级,复杂业务服务的聚合,文件服务的支持,大概8月底完工
4. 是否会支持灰度发布
因为.net core 设计问题,暂时无法做到surging 灰度发布, 已将问题提交给coreclr,现已得到解决,等到3.0发布后,surging 也会开始支持灰度发布。
基于 Zookeeper 和 Consul 多注册中心集群支持
Surging 可以支持pull 和 push 两种方式来更新服务路由,而这两种方式是由consul 和zookeeper 来实现的,而pull 是利用心跳的方式,而 push 是利用Watch 的机制,而 同时 注册中心可以支持向多个注册中心注册服务路由,以同步注册服务。当基于pull 和watch更新的时候,可以通过随机算法来负载获取最新的服务路由来更新本地路由,可以通过以下代码配置多注册中心
Consul (surgingSettings.json):
"Consul": {
"ConnectionString": "${Register_Conn}|127.0.0.1:8500,127.0.0.1:9500",
"SessionTimeout": "${Register_SessionTimeout}|50",
"RoutePath": "${Register_RoutePath}",
"ReloadOnChange": true,
"EnableChildrenMonitor": false
}
Zookeeper(surgingSettings.json)
|
ApiGateway
"Register": {
"Provider": "Consul",
"Address": "${Register_Conn}|127.0.0.1:8500,127.0.0.1:9500"
}
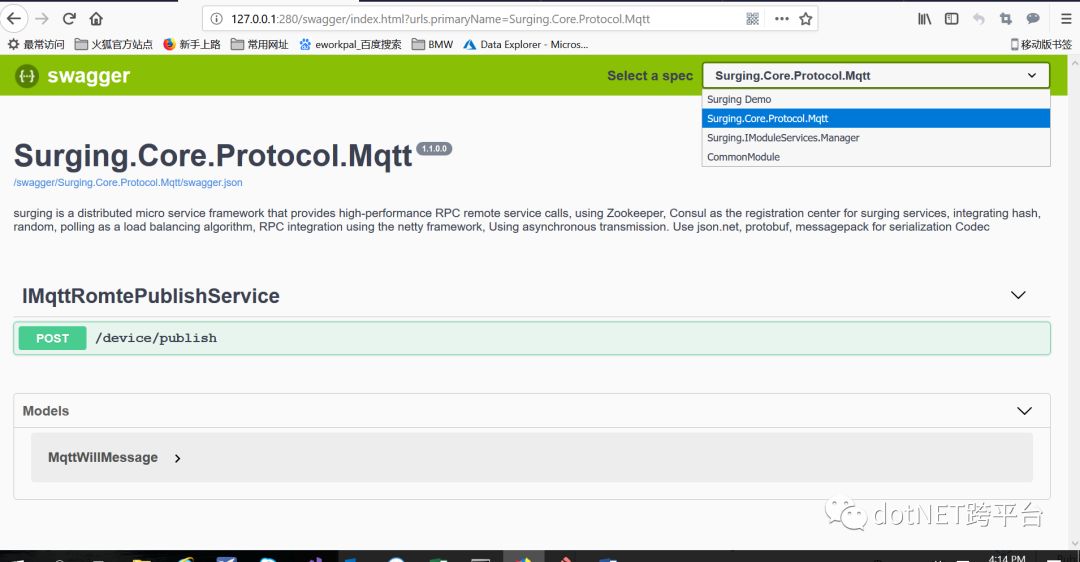
基于swagger 利用业务模块生成API文档
ASP.NET Core Web API 使用Swagger 可以生成在线帮助测试文档,而surging 维护了一套 基于surging 的swagger 的引擎组件,以便支持业务模块使用Swagger 生成在线帮助测试文档。具体可以按照以下代码进行配置:
|
而针对于业务模块生产的测试文档,我们可以通过设置AssemblyInfo.cs,具体代码如下:
|
界面生成如下:
总结
希望大家研究下surging ,surging 会让你对.NET CORE微服务有个全新的认识,也希望大家大力宣传,让surging 发展越来越好。
原文地址:https://www.cnblogs.com/fanliang11/p/10782854.html
.NET社区新闻,深度好文,欢迎访问公众号文章汇总 http://www.csharpkit.com 




)
)





)


)
)


)
