传送门
文章目录
- 题意:
- 思路:
题意:
给nnn个数,让你构造一个尽可能大的矩阵,其中每个点所在的行和列都不含相等元素。
思路:
假设构造的答案矩阵大小为a×ba×ba×b且a<=ba<=ba<=b,那么我们可以知道其中最大的相等元素的个数一定<=a<=a<=a,否则一定不能保证每行每列都不相等。
那么我们就可以[1,n][1,n][1,n]枚举最大的出现次数即aaa,让后假设选出的元素个数为tottottot,那么b=⌊tota⌋b=\left \lfloor \frac{tot}{a} \right \rfloorb=⌊atot⌋,让后取一个最大的就行了。
现在知道矩阵大小a×ba×ba×b了,下面考虑怎么构造答案。
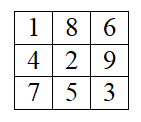
这里直接盗了题解的图了,顺便先把构造方法说了。假设当前位置在(x,y)(x,y)(x,y),那么下一个位置就是((x+1)moda,(y+1)modb)((x+1)\bmod a,(y+1)\bmod b)((x+1)moda,(y+1)modb),当然如果a∗aa*aa∗a的矩阵的话,这样写会一直在主对角线上跑,我们特判一下当前位是否填过了,如果填过的话就x=(x+1)modax=(x+1)\bmod ax=(x+1)moda即可。
其实一开始想到了这样按照斜着填,但是不知道怎么走才能保证自己的想法能实现出来。
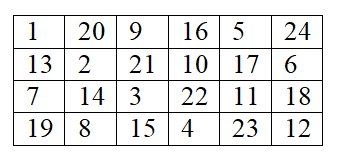
题解((x+1)moda,(y+1)modb)((x+1)\bmod a,(y+1)\bmod b)((x+1)moda,(y+1)modb)这样很巧妙,如下面4×64×64×6的矩阵,填完5,65,65,6再填7,87,87,8的时候正好保证了这四个元素在不同的行。可以证明每个点所在的行和列都不含相等元素。

)
 E. Jeremy Bearimy dfs + 思维)

 E(贪心,bfs))
 D. A Game with Traps 贪心 +二分)


 E(数学))

 D)

)



)


)