C#规范整理·泛型委托事件

基于泛型，我们得以将类型参数化，以便更大范围地进行代码复用。同时，它减少了泛型类及泛型方法中的转型，确保了类型安全。委托本身是一种引用类型，它保存的也是托管堆中对象的引用，只不过这个引用比较特殊，它是对方法的引用。事件本身也是委托，它是委托组，C#中提供了关键字event来对事件进行特别区分。
一旦我们开始编写稍微复杂的C#代码，就肯定离不开泛型、委托和事件。

640?wx_fmt=png

1.总是优先考虑泛型

泛型的优点是多方面的，无论是泛型类还是泛型方法都同时具备可重用性、类型安全和高效率等特性，这都是非泛型类和非泛型方法无法具备的

2.避免在泛型类型中声明静态成员

实际上，随着你为T指定不同的数据类型，MyList＜T＞相应地也变成了不同的数据类型，在它们之间是不共享静态成员的。
但是若T所指定的数据类型是一致的，那么两个泛型对象间还是可以共享静态成员的，如上文的list1和list2。但是，为了规避因此而引起的混淆，仍旧建议在实际的编码工作中，尽量避免声明泛型类型的静态成员。
非泛型类型中的泛型方法并不会在运行时的本地代码中生成不同的类型。
例如: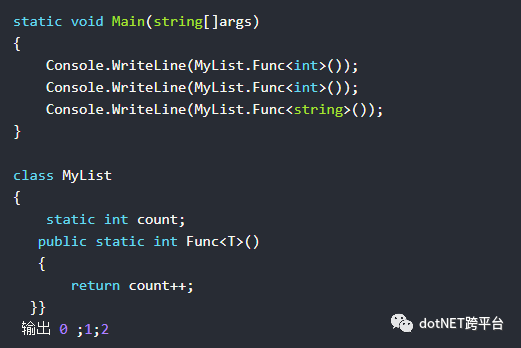

3.为泛型参数设定约束

在编码过程中，应该始终考虑为泛型参数设定约束。约束使泛型参数成为一个实实在在的“对象”，让它具有了我们想要的行为和属性，而不仅仅是一个ob-ject。

指定约束示例：

指定参数是值类型。（除Nullable外） where T:struct
指定参数是引用类型。 where T:class
指定参数具有无参数的公共构造方法。 where T:new()
注意，CLR目前只支持无参构造方法约束。
指定参数必须是指定的基类，或者派生自指定的基类。
指定参数必须是指定的接口，或者实现指定的接口。
指定T提供的类型参数必须是为U提供的参数，或者派生自为U提供的参数。 where T:U
可以对同一类型的参数应用多个约束，并且约束自身可以是泛型类型。

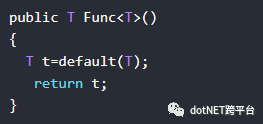
4.使用default为泛型类型变量指定初始值

有些算法，比如泛型集合List＜T＞的Find算法，所查找的对象有可能会是值类型，也有可能是引用类型。在这种算法内部，我们常常会为这些值类型变量或引用类型变量指定默认值。于是，问题来了：值类型变量的默认初始值是0值，而引用类型变量的默认初始值是null值，显然，这会导致下面的代码编译出错：

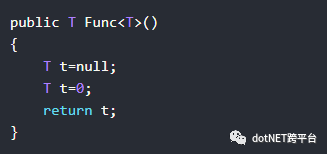
640?wx_fmt=png

代码"T t=null；"在Visual Studio编译器中会警示：错误1不能将Null转换为类型形参“T”，因为它可能是不可以为null值的类型。请考虑改用“default(T)”.
代码"T t=0；"会警示：错误1无法将类型“int”隐式转换为“T”。
改进

640?wx_fmt=png

5.使用FCL中的委托声明

要注意FCL中存在三类这样的委托声明，它们分别是：Action、Func、Predicate。尤其是在它们的泛型版本出来以后，已经能够满足我们在实际编码过程中的大部分需要。下面是这三类委托声明的简要描述。
我们应该习惯在代码中使用这类委托来代替自己的委托声明。
除了Action、Func和Predicate外，FCL中还有用于表示特殊含义的委托声明。

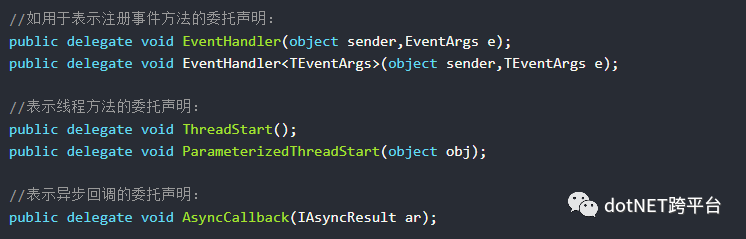
640?wx_fmt=png

在FCL中每一类委托声明都代表一类特殊的用途，虽然可以使用自己的委托声明来代替，但是这样做不仅没有必要，而且会让代码失去简洁性和标准性。在我们实现自己的委托声明前，应该首先查看MSDN，确信有必要之后才这样做。

6.使用Lambda表达式代替方法和匿名方法

在实际的编码工作中熟练运用它，避免写出烦琐且不美观的代码。

7.小心闭包中的陷阱

如果匿名方法（Lambda表达式）引用了某个局部变量，编译器就会自动将该引用提升到该闭包对象中，即将for循环中的变量i 修改成了引用闭包对象（编译器自动创建）的公共变量i。
示例如下：

640?wx_fmt=png

以上结果全部输出5；
另外一种实现方式；

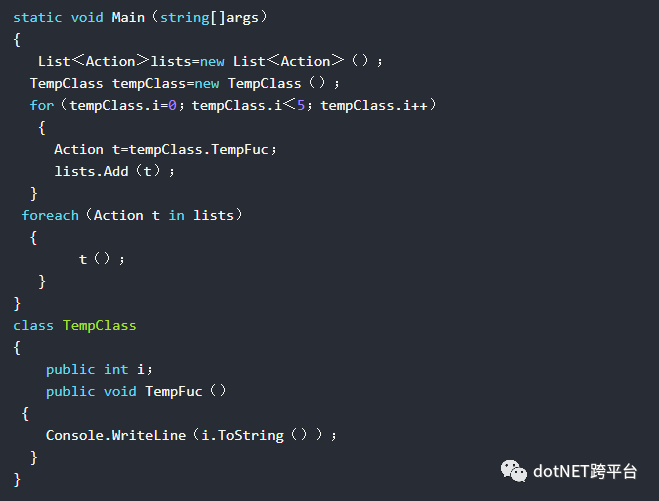
640?wx_fmt=png

Copy

这段代码所演示的就是闭包对象。所谓闭包对象，指的是上面这种情形中的TempClass对象（在第一段代码中，也就是编译器为我们生成的“＜＞c__DisplayClass2”对象）。如果匿名方法（Lambda表达式）引用了某个局部变量，编译器就会自动将该引用提升到该闭包对象中，即将for循环中的变量i修改成了引用闭包对象的公共变量i。这样一来，即使代码执行后离开了原局部变量i的作用域（如for循环），包含该闭包对象的作用域也还存在。理解了这一点，就能理解代码的输出了。

8.了解委托的本质

理解C#中的委托需要把握两个要点：

委托是方法指针。
委托是一个类，当对其进行实例化的时候，要将引用方法作为它的构造方法的参数。

9.使用event关键字为委托施加保护

首先没有event加持的委托，我们可以对它随时进行修改赋值，以至于一个方法改动了另一个方法的委托链引用，比如赋值为null，另外一个方法中调用的时候将抛出异常。
如果有event加持的时候，我们修改的时候，比如

fl.FileUploaded=null;
fl.FileUploaded=Progress;
fl.FileUploaded(10);

以上代码编译会出现错误警告：
事件 “ConsoleApplication1.FileUploader.FileUploaded ”
只能出现在+=或-=的左边（从类型“ConsoleApplication1.FileUploader”中使用时除外）

10.实现标准的事件模型

有了上面的event加持，但是还不能够规范。
EventHandler的原型声明：

public delegate void EventHandler(object sender,EventArgs e);

微软为事件模型设定的几个规范：

委托类型的名称以EventHandler结束；
委托原型返回值为void；
委托原型具有两个参数：sender表示事件触发者，e表示事件参数；
事件参数的名称以EventArgs结束。

11.使用泛型参数兼容泛型接口的不可变性

让返回值类型返回比声明的类型派生程度更大的类型，就是“协变”。
编译器对于接口和委托类型参数的检查是非常严格的，除非用关键字out特别声明，不然这段代码只会编译失败。比如下例
例如：

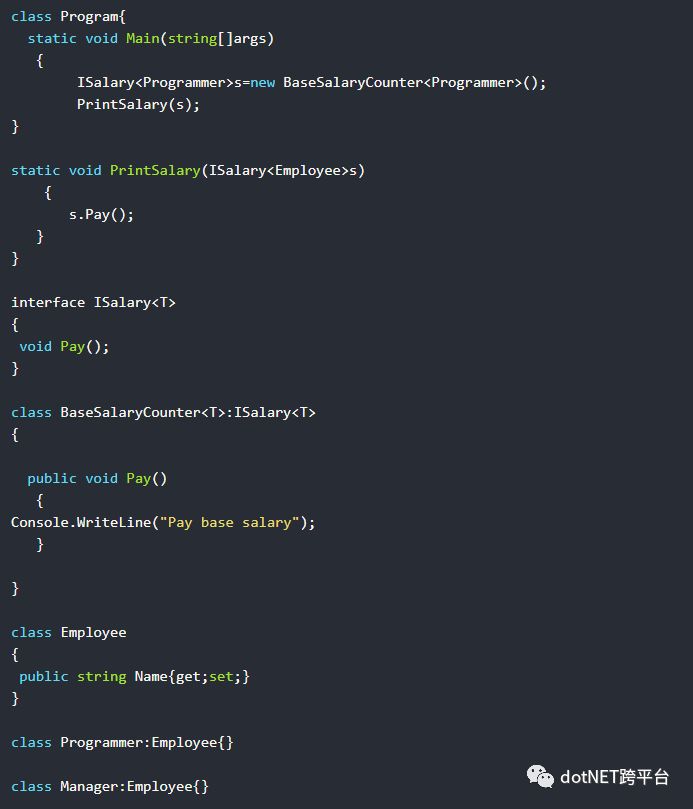640?wx_fmt=png 报错：无法从“ConsoleApplication4.ISalary<ConsoleApplication4.Programmer>”转换为“ConsoleApplication4.ISalary<ConsoleApplication4.Employee>”

要让PrintSalary完成需求，我们可以使用泛型类型参数：

static void PrintSalary<T>(ISalary<T>s)
{ 
 s.Pay();
}

实际上，只要泛型类型参数在一个接口声明中不被用来作为方法的输入参数，我们都可姑且把它看成是“返回值”类型的。所以，泛型类型参数这种模式是满足“协变”的定义的。但是，只要将T作为输入参数，便不满足“协变”的定义了。如：

interface ISalary<out T>
{ 
void Pay(T t);
}

编译会提示：差异无效:类型参数“T”必须是在“ISalary.Pay(T)”上有效的逆变式。“T”为协变。

12.让接口中的泛型参数支持协变

除了11中提到的使用泛型参数兼容泛型接口的不可变性外，还有一种办法就是为接口中的泛型声明加上out关键字来支持协变。
out关键字是FCL 4.0中新增的功能，它可以在泛型接口和委托中使用，用来让类型参数支持协变性。通过协变，可以使用比声明的参数派生类型更大的参数。通过下面例子我们应该能理解这种应用。
比如：

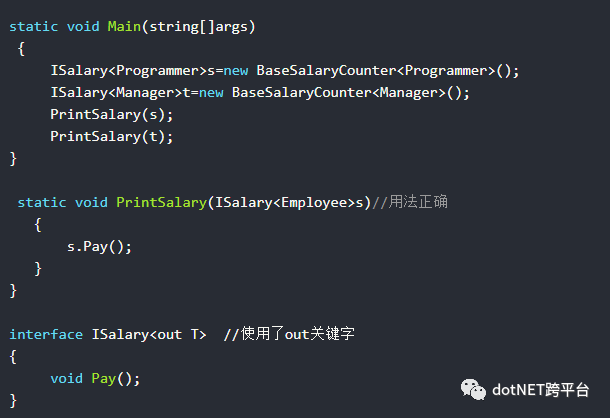
640?wx_fmt=png

Copy

FCL 4.0对多个接口进行了修改以支持协变，如IEnumerable＜out T＞、IEnumerator＜out T＞、IQuerable＜out T＞等。由于IEnumerable＜out T＞现在支持协变，所以上段代码在FCL 4.0中能运行得很好。
在我们自己的代码中，如果要编写泛型接口，除非确定该接口中的泛型参数不涉及变体，否则都建议加上out关键字。协变增大了接口的使用范围，而且几乎不会带来什么副作用。

13.理解委托中的协变

委托中的泛型变量天然是部分支持协变的。
比如：

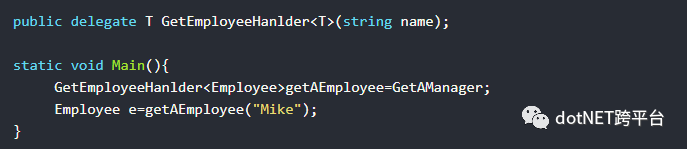
640?wx_fmt=png

因为存在下面这样一种情况，所以编译通不过：

要让上面的代码编译通过，同样需要为委托中的泛型参数指定out关键字：

public delegate T GetEmployeeHanlder<out T>(string name);

FCL 4.0中的一些委托声明已经用out关键字来让委托支持协变了，如我们常常会使用到的：

public delegate TResult Func<out TResult>()和
public delegate TOutput Converter<in TInput,out TOutput>(TInput input)

14.为泛型类型参数指定逆变

逆变是指方法的参数可以是委托或泛型接口的参数类型的基类。FCL 4.0中支持逆变的常用委托有：

Func<in T,out TResult>
Predicate<in T>
//常用泛型接口有：
IComparer<in T>

举例：

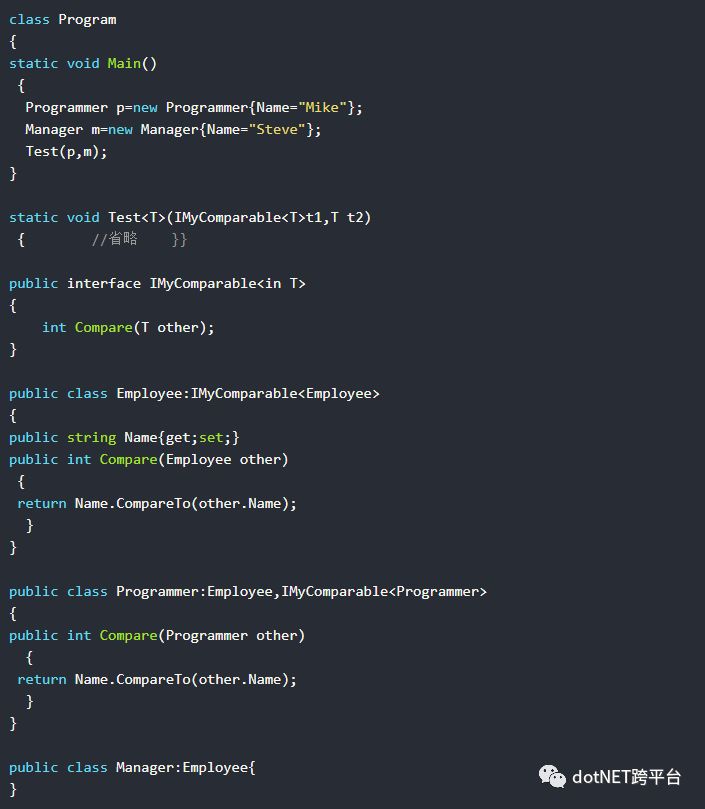
640?wx_fmt=png

在上面的这个例子中，如果不为接口IMy-Comparable的泛型参数T指定in关键字，将会导致Test（p, m）编译错误。由于引入了接口的逆变性，这让方法Test支持了更多的应用场景。在FCL4.0之后版本的实际编码中应该始终注意这一点。

640?wx_fmt=jpeg

总结

如有需要，上一篇的《C#规范整理·集合和Linq》也可以看看！

深入理解协变和逆变传送门《逆变与协变详解》

原文地址：https://www.cnblogs.com/zhan520g/p/11026778.html

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com
640?wx_fmt=jpeg