传送门

题意：

懒得写了，直接贴图了。

思路：

遇事不决画成图，考虑将$i$向$p[i]$连一个边，可以发现每个点入度为$1$，出度为$1$，所以画出来是若干个环，比如说样例三画出来就是这样的(这里只画了一个环)

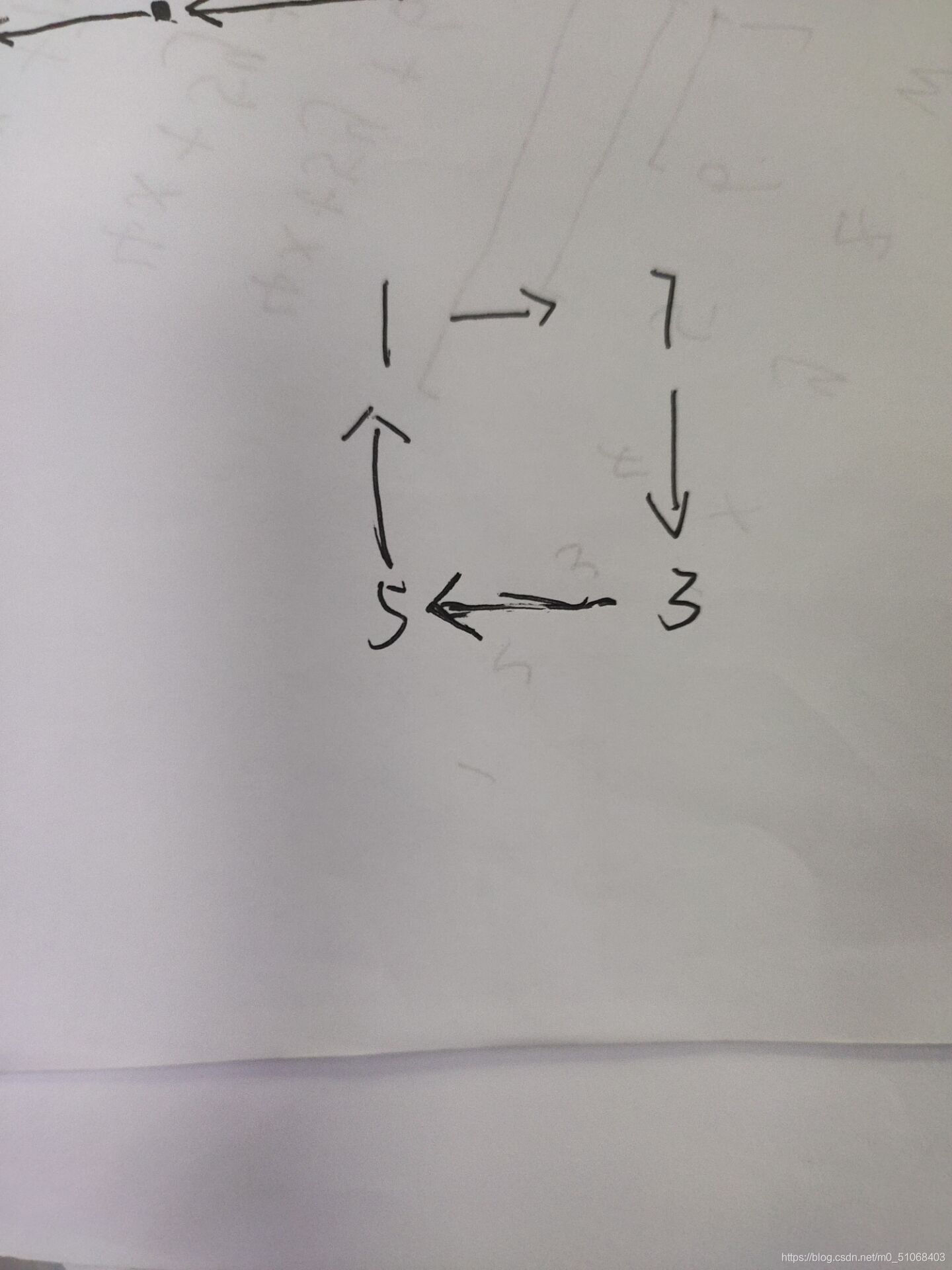
上图为$p^1$的情况，进而可以发现，当$p$的幂次为$k$的时候，就是将每个数与其往下数$k$个数之间连边，比如$p^2$的图如下所示：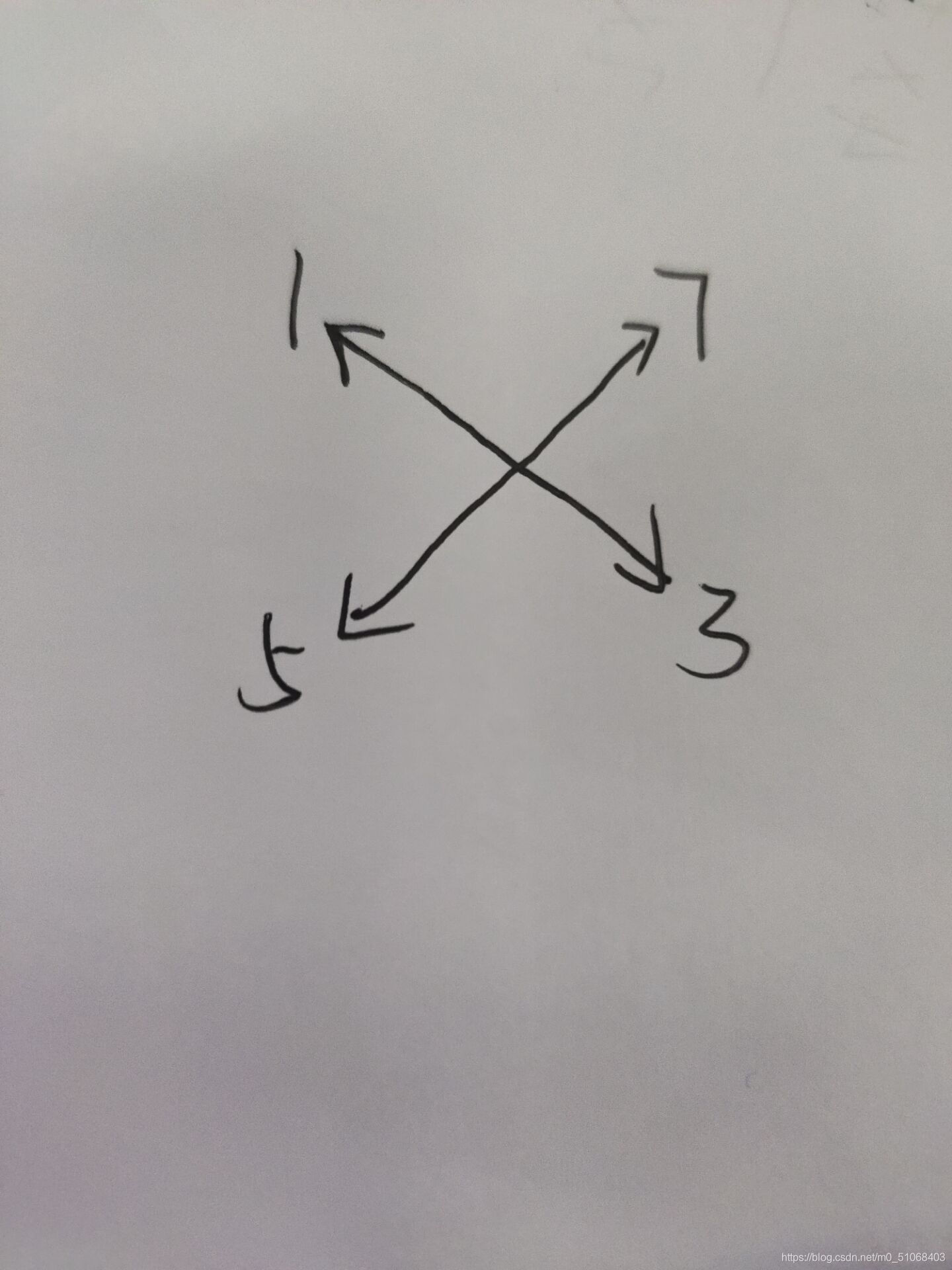
所以我们假设环的长度为$len$，那么可以发现只有$len\mathrm{m}\mathrm{o}\mathrm{d}k=0$的$k$才有意义，其他的连边方式都是$k$的某种情况，所以我们只需要枚举$len$的因子，让后判断$pos\mathrm{m}\mathrm{o}\mathrm{d}diver$相同的位置颜色是否一样就好了，取一个最小的因子即可。
这里写的麻烦了，完全可以用筛法替代我这个垃圾写法。
复杂度$O(n\sqrt{n})$。

// Problem: D. Infinite Path
// Contest: Codeforces - Educational Codeforces Round 84 (Rated for Div. 2)
// URL: https://codeforces.com/contest/1327/problem/D
// Memory Limit: 256 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)//#pragma GCC optimize("Ofast,no-stack-protector,unroll-loops,fast-math")
//#pragma GCC target("sse,sse2,sse3,ssse3,sse4.1,sse4.2,avx,avx2,popcnt,tune=native")
//#pragma GCC optimize(2)
#include<cstdio>
#include<iostream>
#include<string>
#include<cstring>
#include<map>
#include<cmath>
#include<cctype>
#include<vector>
#include<set>
#include<queue>
#include<algorithm>
#include<sstream>
#include<ctime>
#include<cstdlib>
#define X first
#define Y second
#define L (u<<1)
#define R (u<<1|1)
#define pb push_back
#define mk make_pair
#define Mid (tr[u].l+tr[u].r>>1)
#define Len(u) (tr[u].r-tr[u].l+1)
#define random(a,b) ((a)+rand()%((b)-(a)+1))
#define db puts("---")
using namespace std;//void rd_cre() { freopen("d://dp//data.txt","w",stdout); srand(time(NULL)); }
//void rd_ac() { freopen("d://dp//data.txt","r",stdin); freopen("d://dp//AC.txt","w",stdout); }
//void rd_wa() { freopen("d://dp//data.txt","r",stdin); freopen("d://dp//WA.txt","w",stdout); }typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> PII;const int N=200010,mod=1e9+7,INF=0x3f3f3f3f;
const double eps=1e-6;int n;
int a[N],p[N],c[N],col[N],cnt[N];
bool st[N];
vector<int>v,diver;int solve() {int len=v.size();diver.clear();for(int i=1;i<=len/i;i++) {if(len%i==0) {diver.pb(i);if(1ll*i*i!=len) diver.pb(len/i);}}int ans=INF;for(auto x:diver) {for(int i=0;i<v.size();i++) cnt[i%x]=len/x;for(int i=0;i<v.size();i++) {if(col[i%x]==-1) col[i%x]=c[v[i]];else if(col[i%x]!=c[v[i]]) cnt[i%x]--;}for(int i=0;i<v.size();i++) if(cnt[i%x]==len/x) ans=min(ans,x);for(int i=0;i<v.size();i++) col[i%x]=-1;}return ans;
}int main()
{
//	ios::sync_with_stdio(false);
//	cin.tie(0);memset(col,-1,sizeof(col));int _; scanf("%d",&_);while(_--) {scanf("%d",&n);for(int i=1;i<=n;i++) scanf("%d",&p[i]),st[i]=0;for(int i=1;i<=n;i++) scanf("%d",&c[i]);int ans=INF;for(int i=1;i<=n;i++) if(!st[i]&&!st[p[i]]) {if(i==p[i]) {ans=1; break;}v.clear();v.pb(i); v.pb(p[i]); st[i]=1; st[p[i]]=1;int now=p[p[i]];while(!st[now]) {v.pb(now);st[now]=1;now=p[now];}int len=v.size();ans=min(ans,solve());}printf("%d\n",ans);}return 0;
}
/**/