最近一时兴起，研究了一些文件管理的方法论和笔记管理类的知识，自己想到一些不错的方法及落地方案，可能对一部分朋友来说，这些方法和工具的落地会有一些共鸣，故简单给大家做一下分享。

跨界应用：数据表结构应用衍生至文件或笔记管理中

在我们日常的Excel表的数据管理中，有一种表是维度类的实体表，这些表结构是用于描述一个现实实体的属性构成，如企业数据中的产品表、员工表、店铺表、供应商表等。

我们每天使用Excel的Vlookup函数时，多数是指向这些维度表去查询额外的属性信息用于主表的一些分类属性使用。

这些维度表一般来说是一行记录代表一个实体，其中一列是实体的唯一码，其他列是对这个实体的详细描述，如产品表，我们的产品ID是A001，对应的属性列有产地、供应商、生产日期、材质、风格、尺寸、产品大类、中类、小类等。

换到我们对文件或我们日常的笔记上来看，其实我们可以把文件或笔记当作我们的实体来维护，一个文件就是我们一个实体的实例，当然有唯一名字最好，有其他的一些描述这个文件的属性产生。

有些属性是我们系统可以生成的如创建日期、修改日期、文件大小等，大量我们想用来更深入描述这个文件的属性，在大多数人的日常管理中，使用的是文件夹式的管理。用不同文件夹来代表不同的属性。

同样地笔记类也可以类似地管理，如有道云笔记等，一样可以有文件夹式的管理存在，文件夹可以有嵌套结构，可以一个文件夹下包含许多的子文件夹，可以无限地分类下去。

最终我们对文件的描述信息，多数就落到了文件夹上，文件夹名称类似我们数据表中的除实体唯一列以外的其他属性列的作用。

文件夹式管理带来的弊端很明显

通过上述的分析，我们可以看到，文件夹给我们带来了文件额外属性的标注，如文件属于【个人】、【工作】文件夹，同时在【工作】文件夹下，按笔者本身的工作属性，会分出服务对象的不同公司的文件夹如【公司A】、【公司A】、【公司C】等，在某个【公司A】上，再分出【项目需求】、【开发内容】、【文件交付】等文件夹，若一个【公司A】做了好几个项目，想着把资料再细分一下，可能又要分出【项目A】、【项目B】等文件夹，再或者想再分一下和某些人打交道产生的文件，又有【某A】、【某B】等文件夹。

通过上面的例子可以看到，我初衷是为了更好地管理文件，结果是我个人已经深深地陷入到这处无止境的分类中，而这些分类，耗费了大量的思考，同时也让有完美主义倾向的人感到很绝望，为了应该公司下面先放项目还是人员类别而纠结万分。

本来按数据管理的角度来看，一个实体对其定义尽可能地细化，对于后续我们使用时会带来很多的好处，可以更精细化地进行数据分析。为何来到文件的定义上，最终却变得这么吃力不讨好。

分类的事情上很纠结，同样地我们重新来定位这个文件，将其找出来，也是非常痛苦的过程。

虽然说可以有Everything这样的搜索神器帮助，在这一点上，笔者也没有少花功夫，从TotalCommander、Listary、XYploerer，还有无数不记得曾经被吸引去花时间研究过的效率工具，都对这上面的结果无解。

当然Excel催化剂自己也开发了好多关于文件类的功能增强，还是没打破这个恼人的文件夹分类问题。最终还会有很大的挫败感，觉得自己真的太混乱了，从生活中的混乱衍生到了电子化的资料管理的混乱。

混乱的文件夹式管理文件解药在哪里？

诚然，看到这里的读者习惯性地会想到软文开始了，一般地文件套路就是这样，列出一堆问题来，然后就开始说某某产品可以解决。

Excel催化剂老读者都知道，在Excel催化剂的文章里，是极少有推广性地去推荐什么东西来获取收益。希望读者们看到下面的解决方式时，可以知道笔者的动机，仅仅是为了分享优质资讯而已，并且能够给大家推荐的时候，已经是自己经过漫长地摸索失败后才找到的一些有价值信息。

在今年年初，看到了赵金彪老师翻译过的一本书，《掌控你的工作！——巧用Outlook极速提升工作效》，并且赵老师也根据这本书的理论，自己开发了一款Outlook插件。

诚然这本书是讲如何管理工作中的邮件和对工作进行任务管理，使用的工具是Outlook软件。

并非因为Outlook有多优秀，每个人都可以使用了Outlook之后就可以把邮件管理得很好，相反邮件通常是一个灾难性地存在，特别是在外企中。

此处不展开，长话短说，就是从MYN这套对邮件的管理思想中，到现在的日常文件，这套理论仍然适用。

MYN管理邮件是思想是无需对邮件进行分类，类似我们文件管理一样，邮件同样可以进行分类，一个文件和一封邮件，何等类似。它里面只分出了收件箱和已处理两个邮件文件夹。所有处理过的邮件，直接拖到已处理文件夹中，保持收件箱是清空的状态。

这样的思路，我应用到文件管理中，就是当天的使用的文件，都放到了桌面上（无论什么样的软件，保存文件选择桌面都是非常容易做到的）。

一天的文件往来，经过整理归档后，应该是这样的桌面效果，笔者现在也努力去践行清空桌面的习惯。

但问题来了，邮件一般可以全文搜索，邮件内容基本在标题和正文中可以体现，使用搜索可以轻松获得，但文件的话，能够达到同样的搜索体验的话，只能在文件名上写上足够详细的内容标识，才能够让文件可以使用Everything这样的搜索神器快速搜索到。

文件的标签式管理替代文件夹管理

回顾我们日常的数据实体表结构，是由许多列组成的属性扩展，同一行的内容描述了某个实体对象的许多的属性。

在文件管理上，理当也像实体表一样管理，才能克服我们前面提到的文件夹管理的分类困境。

源于对于物理世界的物体的管理方式，在电子化数据文件中，也沿用了它的方式，如我们物理世界中，存放一个文件或物体如仓库里的某物品，需要对其划分库位、货架层，货架位置等，最终物品只会在物理世界中某一个位置点出现。

在找寻物体时，也用类似文件夹式的从最源头的分类开始找起，先看第几个区的库位大位置，再看第几排，再看第几层，再看其他细小分类等，最终找到我们的物品。

但在电子化世界中，我们有比以上更快的方式触达我们最终要找寻的文件或其他资料，就是搜索。

通过搜索，我们可以跳出多级的结构，快速到达我们的目的地-目标文件所在处，并且可以轻松对其选择、打开、复制等操作。

现在知识大爆炸时代，不懂用搜索功能，是多少吃亏的事情，所以对海量数据（文件），我们更应该使用的方式是搜索方式（特定场景下，对文件存放位置较为熟悉，且文件近期使用过，并且用某些快捷方式可以快速到达目标文件所在文件夹，也可以使用文件夹方式来查找）。

搜索的方式要求我们记得文件名的关键字，而关键字的定义就显得非常关键。

现在笔者找到的解决方法是尽可能用标签来处理，防止我们对同一分类下的不同的字词的定义，加深了搜索的难度，毕竟我们本地搜索不像搜索引擎这么智能，可能按语义搜索，多种关键字可以近似搜索的方式查找到。

用标签的方式来定义文件的属性，完全符合了我们实体数据定义的逻辑，一个标签与文件是存在多对多关系，而文件夹方式是一种一对一的关系，一个文件夹路径对应一个文件。

设想一下，我们查找的场景是查找【公司A】、【项目A】下的文件往来或【公司A】下的【需求文档】，我们不必像文件夹式的管理方式，没法一次性找全所有内容或在所有内容清单中查找（因为文件夹是一对一的关系，你只能定义公司到项目或公司到需求文档，而没法同时两种兼顾）。

而使用标签式的管理，类似于我们在写SQL语句时，使用Where的多个条件的And或Or等组合方式完成最终的搜索结构。

如何给文件更好地打上标签

这个是我们上述提及的方法论落地的最为关键之处，没有好的工具完成，纯手工操作，会让我们整个方法论的落地走向死胡同，没有几个人能够坚持下来并能准确地完成文件的标签命名。

同样地这里也引出一款软件TagLyst Next，这个是国人开发的，笔者也尝试找了一大轮和其相关的软件，其同类似师傅是TagSpaces，还有许多同样可以实现文件标签管理的如Tabbles、XYploer、FenrirFS、File Note等。笔者精力有限，很难去完全地熟悉各软件的差异点。有喜爱这个主题的可以一起再交流分享。

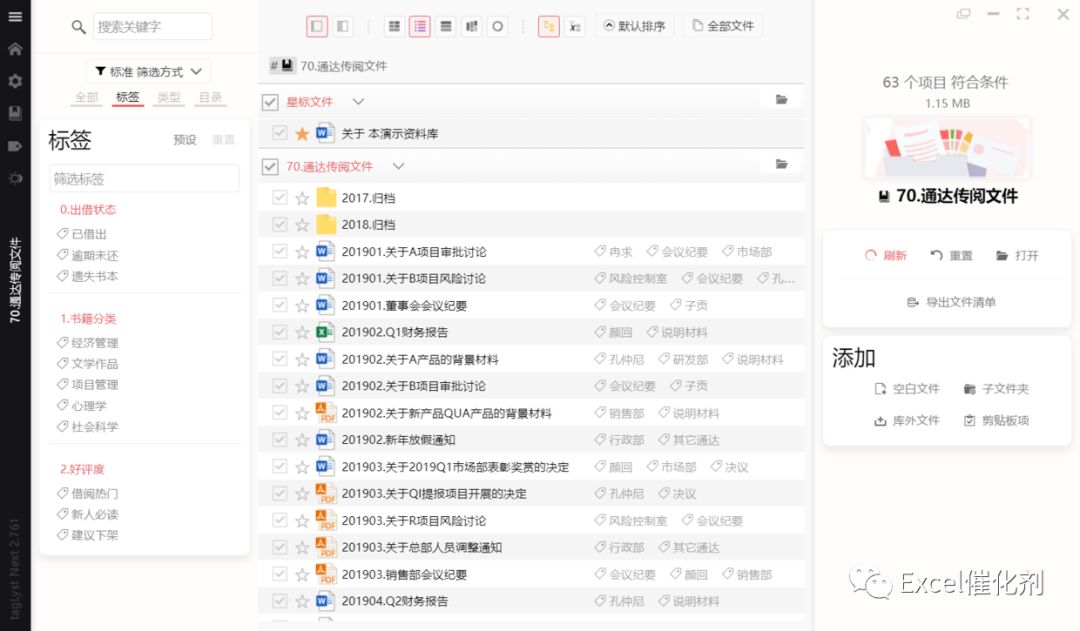
当然笔者也去搜索过一些破解版本，但最后看软件的更新日志，已经放弃找这些破解版本了，Excel催化剂自己同样地开发软件，看到更新日志，就想到软件不断地更新更为值得，起码每个更新都是一点点地进步过程。

最后因为喜爱的原因，向TagLyst运营者要了一个专业版Licence，使用Excel催化剂公众号帮忙推广了一篇文章获得，这也是Excel催化剂唯一的一次使用粉丝的资源作了一次小小的无伤大雅的置换。

也因着下定决心，将文件标签化管理落地，通过练习将其成为自身的文件管理手段，对TagLyst Next的功能学习后，发现其核心的标签管理功能，还存有一些不够友好的地方，也开始向其提一些建议优化，希望后续的版本更加方便。

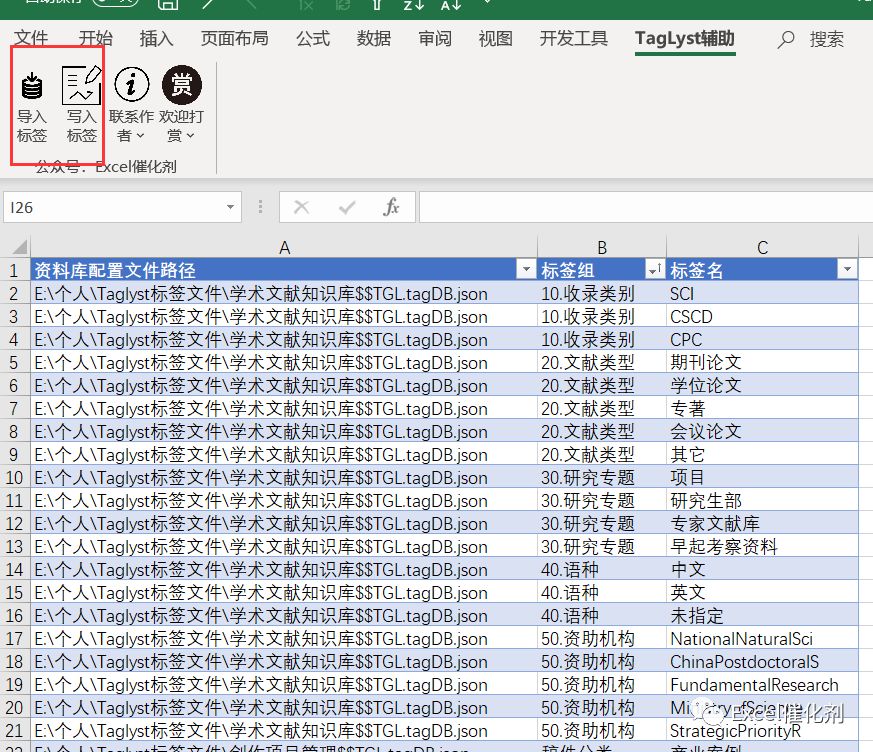
最后，因着软件管理配置信息的天生缺陷，笔者索性使用Excel插件的方式对其标签管理进行增强，而花了一些时间进行了开发，最终可以在Excel环境下对其标签进行维护，并且这套标签将成为我们的所有电子化的资料标签进行复用如有道云笔记等。

此功能使用文档型插件的方式开发，仅对特定的文档生效，因其实际上也仅在维护标签时需要使用，所以也可以让大家感受下文档型的VSTO的优势所在。

一起来探讨标签式文件及资料管理吧

本文篇幅有限，下篇继续分享，有兴趣的朋友们，可以预先熟悉下TagLyst Next这款软件，它有免费版，不是太深度使用的话，免费版可以满足笔者所提及的最核心的文件标签管理功能。

正如Outlook的出现，不会天生就满足MYN的邮件管理思路，同时也需要有像赵老师这样对其理论有深刻理解和实践的人来开发出插件的方式来增强，笔者开发的两个小功能，也是对TagLyst Next标签管理的一大补充，欢迎继续关注，下篇会给大家以视频录制的方式来分享一些使用体验。

标签式文件管理最核心的是标签的定义，欢迎大家一起分享日常的有价值的标签使用，这个无关技术和工具，是非常发散性的，对归纳、分类、抽象性能力强的，可以帮我们做出更棒的标签，然后可以分享出来一起使用。

欢迎加入微信群继续交流分享

最后，给大家两篇不错的文件管理文章，可以一同继续衍生学习参考。