[蓝桥杯2016初赛]剪邮票-dfs+next

[蓝桥杯2016初赛]剪邮票-dfs+next_permutation(好题)

题目描述
如下图, 有12张连在一起的12生肖的邮票。现在你要从中剪下5张来，要求必须是连着的。（仅仅连接一个角不算相连）
在这里插入图片描述

比如，下面两张图中，粉红色所示部分就是合格的剪取。
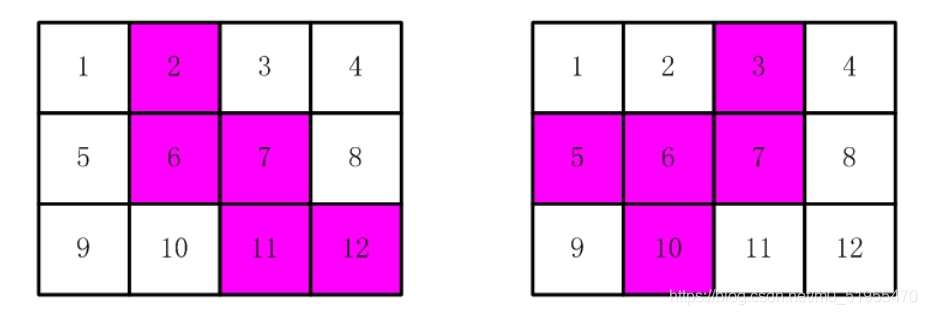
在这里插入图片描述

请你计算，一共有多少种不同的剪取方法。
输出
请填写表示方案数目的整数。

解题思路：
这题不能用dfs，原因是dfs无法处理下面这种情况：
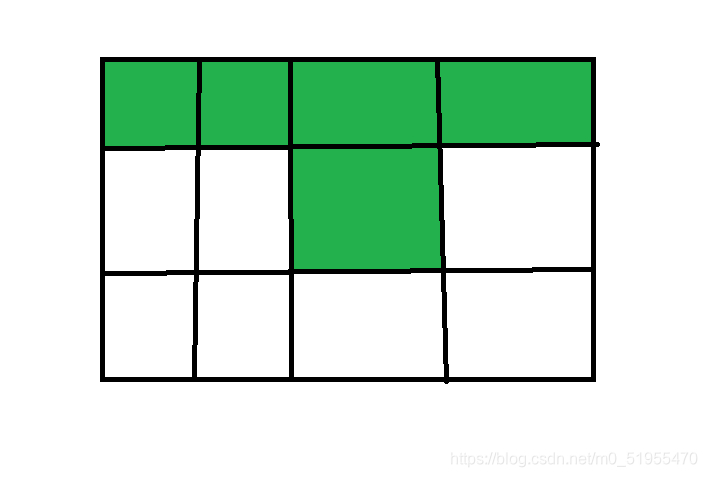
在这里插入图片描述
dfs一路走到底，所以它没办法回头，所以这题不能用dfs，那么我们可以用next_permutation函数枚举所选的5个点，然后用dfs判断是否连通。

代码如下：

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 5;
bool mp[N][N];
int cnt;
int ans;int a[] = {0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1};int dx[] = {0, 0, 1, -1}, dy[] = {1, -1, 0, 0};void dfs(int x, int y) {if (x < 0 || x > 2 || y < 0 || y > 3)return;if (mp[x][y] != 1)return ;cnt++;if (cnt == 5) {ans++;return ;}mp[x][y] = 0;for (int i = 0; i < 4; i++) {int xx = x + dx[i], yy = y + dy[i];dfs(xx, yy);}
}int main() {do {int px, py;for (int i = 0; i <= 2; i++)for (int j = 0; j <= 3; j++) {if (a[i * 4 + j] == 1) {//将一维数组映射到二维数组px = i;py = j;mp[i][j] = 1;} elsemp[i][j] = 0;}dfs(px, py);cnt = 0;} while (next_permutation(a, a + 12));cout << ans << endl;return 0;
}

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 5;int a[] = {0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1};int dx[] = {0, 0, 1, -1}, dy[] = {1, -1, 0, 0};
int cnt ;
int px, py;
int mp[N][N];
int ans;void dfs(int x, int y) {for (int i  = 0; i < 4; i++) {int xx = x + dx[i];int yy = y + dy[i];if (xx < 0 || xx >= 3 || yy < 0 || yy >= 4 || !mp[xx][yy])continue;mp[xx][yy] = 0;cnt++;if (cnt == 5)ans++;dfs(xx, yy);}
}int main() {do {for (int i = 0; i < 3; i++)for (int j = 0; j < 4; j++) {if (a[i * 4 + j] == 1) {mp[i][j] = 1;px =  i;py = j;} elsemp[i][j] = 0;}cnt = 1;mp[px][py] = 0;dfs(px, py);} while (next_permutation(a, a + 12));cout << ans << endl;return 0;
}