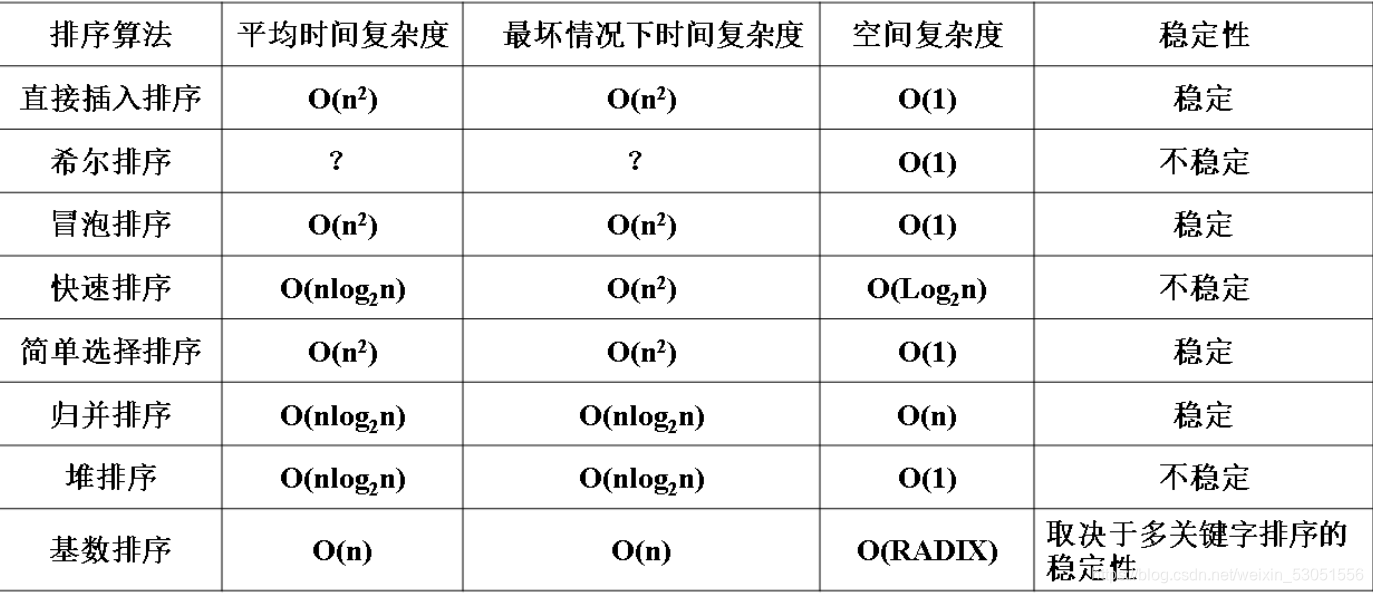
排序 

排序:重点在于对于记录的关键字进行排序,得到按关键字有序记录序列
分为:
    A.内部排序: 排序过程在内存中进行 
    B.外部排序: 待排序记录数据量过大,需要借助外部存储设备
排序的稳定性:排序后有相同关键字的记录顺序不变就是稳定的排序

插入类排序:

1.直接插入排序:

将新加入的记录的关键字与之前的记录关键字从后往前比较,
               若较小,则向前比较,同时进行比较的记录后移一个位置,直到找到小于等于的关键字,插入在其后. 

实例代码如下: 
void InsSort(int r[], int length){//r可以设置为结构数组,这里认为是数组 
    int i,j;
    for(i = 2; i < length; i++){ // i=2开始,i=1为第一个元素,认为是子表,i=0设置为监视哨 
        r[0] = r[i];//将待插入记录存到监视哨中,临时保存 
        j = i - 1;  //i为初始待插入记录位置,i-1为需要比较的记录位置
        while(r[0] < r[j]){
            r[j+1] = r[j];
            j--;
        } 
        r[j+1] = r[0];
    }
} 

优点:算法简单,适用于记录数目较少且基本有序
时间复杂度:O(n^2).

2.折半插入排序:类似于快排

示例代码如下:
void BinSort(int r[], int length){
    int i, x, j;
    int low, high, mid;
    for(i = 2;i <= length; i++){
        x = r[i];
        low = 1;
        high = i - 1;
        while(low <= high){
            mid = (low + high) / 2;
            if(x < r[mid])
                high = mid - 1;
            else
                low = mid + 1;
        }
        for(j = i - 1; j >= low; j--)
            r[j+1] = r[j];
        r[low] = x; 
    }
} 
时间复杂度:O(n^2).
需要比较的次数最大为其折半判定树的深度log2(n)

3.希尔排序:

排序结果,基本有序;又称缩小增量排序;将关键字序列分为若干个子序列,对子序列插入排序

void f1(int r[], int length, int d){//d为这一轮子序列长度(增量) 
    int i, j;
    
    for(i = 1+d; i <= length; i++){
        if(r[i] < r[i-d]){
            r[0] = r[i];
            for(j = i - d; j > 0 && r[j] > r[0]; j -= d){
                r[j + d] = r[j];
            }//如果子序列后者的记录关键字比前小,就复制前者到后者 
            r[j + d] = r[0];//复制要交换的一个到适合的位置 
        }
    }
} 
 
void f2(int r[], int length, int d[], int n){
    for(i = 0; i < n; i++)//d[]为增量数组,n为该数组长度 d[n-1] == 1; 
        f1(r, length, d[i]);
}
时间复杂度:O(n^1.5).
算法不是稳定的 .

交换类排序:

1.冒泡排序(相邻比序法):

反复扫描记录序列,依次交换逆序记录的位置

void BubbleSort(int r[], int n){
    bool change = true;
    int i,j;
    int x = 0;
    for(i = 1; i < n && change; i++){
        change = false;
        for(j = 1; j <= n - i; j++){
            if(r[j]>r[j+1])
            {
                x = r[j];
                r[j] = r[j+1];
                r[j+1] = x;
                change = true;
            }
        }
    }
} 

//下面这种简单些:上升法,不带标记 
void BubbleSort(int r[], int n){
    int i, j, k;
    
    for(i = 0; i < n; i++){
        for(j = n - 2; j >= i; j--){
            if(r[j] > r[j+1]){
                k = r[j];
                r[j] = r[j+1];
                r[j+1] = k;
            }
        }
    } 
}

时间的复杂度:O(n^2). 

2.快排:

原理:一次性可以消除多个逆序来减少耗费时间
找到一个划分元,关键字小的移到前面,大的移到后面,递归在子序列中找出划分元.直到子表长度小于等于1

void QKSort(int r[], int low. int high){
    if(low < high){
        pos = QKPass(r, low, high);//再次快排
        QKSort(r, low, pos -1);
        QKSort(r, pos +1, high); 
    }
} 

一趟快速排序算法: 
int QKPass(int r[], int low, int high){
    int x;
    while(low < high){
        while(low < high && r[high] > x)
            high--;
        if(low < high){
            r[low] = r[high];
            low++;
        }    
        while(low < high && r[low] < x)
            low++;
        if(low < high){
            r[high] = r[low];
            high--;
        }        
    }
    r[low] = x;
    return low;
}
时间复杂度:O(nlog2(n)) 

选择类排序:

1.简单选择排序:

直接从数组中选择最小的记录和第一个记录交换位置,循环

void SelectSort(int r[], int b){
    int i, j, k;
    int x;
    
    for(i = 1; i < n; i++){
        k = i;
        for(j = i+1; j <= n; j++){
            if(r[j] < r[k])//选择最小的记录,得到在数组中的位置 
                k = j;
        }
        if(k != i){
            x = r[i];
            r[i] = r[k];
            r[k] = x;
        }//交换位置 
    }
} 
时间复杂度:O(n^2).

2.树形选择排序(锦标赛排序):

与简单选择排序不同点是,占用空间更多,保留了之前的比较结果
每一个记录看作叶子节点,两两比较,选出最小的为双亲,进一步递归向上,找出根,比较成功后,
该记录对应的叶子节点置为无穷;
进一步两两比较重复上述过程,直到记录全部输出
时间复杂度:O(nlog2(n)). 

3.堆排序:

排序过程中把向量中储存的数据看作一颗完全二叉树来进行操作
重建堆:
    大堆,筛选最大的元素出去,然后最后的元素补根节点,调整堆使最大的元素在最上面 
void sift(Type r[], int k, int m){
    //r[k...m]是以r[k]为根的完全二叉树,调整r[k]使之满足堆的性质 
    int i, j, t, x;
    
    t = r[k];
    x = r[k].key; 
    i = k;
    j = 2 * k;//j指向t的左孩子
    bool finished = false;
    
    while(j <= m && !finished){
        if(j + 1 <= m && r[j].key < r[j+1].key){
            j++;
        }//得到左右孩子中记录关键字较大的位置坐标 
        if(x >= r[j].key) //如果满足堆的性质,上面的比孩子大 
            finished = true;
        else{
            r[i] = r[j];
            i = j;
            j = 2 * i;
        }
    } 
    r[i] = t;
} 

建初堆:
void crt_heap(Type r[], int n)
{
    //对r[]建立堆, n为数组长度
    int i;
    for(i = n / 2; i >= 1; i--)//i指向最后一个非叶子节点 
        sift(r, i, n); 
 } 

堆排序算法:
void HeapSort(Type r[], int n)
{
    crt_heap(r, n);
    
    for(i = n;  i>= 2 ;--i){
        r[0] = r[1];
        r[1] = r[i];
        r[i] = r[0];//最后一个元素和第一个元素交换位置,把最大的换到最后面去,以此达到升序排列x 
        sift(r, 1, i-1);
    }
 } 

时间复杂度:O(nlog2(n)).
算法是不稳定的, 空间复杂度O(1) .

归并类排序:将两个或两个以上的有序表合并成一个表

两个有序子序列合并算法: 
void Merge(Type r1[], int low, int mid, int high, Type r2[])
{
    //r1[low...mid]和r1[mid+1,..high]分别按照关键字有序排列 ,合并存放在r2[]中
    int i, j, k;
    i = low;
    j = mid + 1;
    k = low;
    
    while(i <= mid && j <= high){
        if(r1[i].key <= r1[j].key)
            r2[k++] = r[i++];
        else
            r2[k++] = r[j++];
    }
    while(i <= mid){
        r2[k++] = r1[i++];
    }
    while(j <= high){
        r2[k++] = r1[j++];
    }
 } 

路归并排序的递归算法:
void MSort(Type r1[], int low, int high, Type r3[])
{
    //r1[low...high]排序后放在r3[low...high] 中, r2为辅助空间
    Type *r2;
    int mid;
    
    
    r2 = (Type *)malloc(sizeof(Type) * (high - low + 1));
    if(low == high) r3[low] = r1[low];
    //这个是递归最终退出条件
    else{//r1前半段放到r2前半段中,同理对于后半段,再将r2合并排序 
        mid = (low + high) / 2;
        MSort(r1, low, mid, r2);
        MSort(r1, mid + 1, high, r2); 
        Merge(r2, low, mid, high, r3);
    } 
    free(r2);
 } 

调用:
void MergeSort(Type r[], int n){
    MSort(r, 1, n, r);
} 

分配类排序:

核心是分配和收集,利用关键字的优先级进行排序的思想 

高位优先排序:

比如桥牌,先比较花色在比较面值;比如学号,比较级,院,班,号;

低位优先排序:

链式基数排序

思想:基于"分配"和"收集"的操作, 将单关键字转化为多关键字排序
将链表作为存储结构, 待排序记录以指针相连,构成链表;
分配:按照关键字取值分配记录到链队列相应队列中,每个队列关键字取值相同
收集:按照关键字大小,从小到大,将队列首尾相接连接成一个链表;
重复上述步骤..

定义:
//待排序记录结点
typedef struct node{
    int data;//比如说一个三位数 
    struct node *next;
}TNode;

//队列首尾指针
typedef struct{
    node *front;
    node *rear;
}TPointer; 

//根据数组R[](已经存在元素),构建带头结点待排序记录链表
TNode *create_list(int R[], int n){
    
    TNode *p, *ph;
    //p为每一个存了记录的结点, ph为头结点
    ph = (TNode *)malloc(sizeof(TNode));
    if(!ph) return NULL; 
    ph->next = NULL;
    
    int i;
    for(i = 0; i < n; i++){
        p = (TNode *)malloc(sizeof(TNode));
        if(!p) return NULL;
        
        p->data = R[i];
        //头插法插入 
        p->next = ph->next;
        ph->next = p;
    }
    return ph;//返回头结点 
} 

#define N 10
//分配算法,对三位数的记录序列按照关键字低位排序分配 
void dispatch(TNode *ph, TPointer *Q, int d){    
    //ph存记录, Q队列:存指针,d根据关键字到那一趟取值不同    
    TNode *p = NULL;//作为辅助空间拆分ph 
    int i, idx;
    
     
    //初始化Q
    for(i = 0; i < N; i++){
        Q[i].front = NULL;
        Q[i].rear = NULL; 
    } 
    
    p = ph->next;
    if(p){
        ph->next = p->next;
        p->next = NULL;
    }//第一个记录被单独拆到p里面
    
    while(p){
        idx = p->data;
        for(i = 0; i < d; i++)
            idx = idx / N;
        //第一趟排序,d = 0
        idx = idx % N;
        
        //根据关键字分配到Q中
        if(Q[idx].front = NULL){
            Q[idx].front = p;
            Q[idx].rear = p;
        } 
        else{//尾插法 
            Q[idx].rear->next = p;
            Q[idx].rear = p;
        }
        p = ph->next;
        if(p){//拆,直到拆完 
            ph->next = p->next;
            p->next = NULL;
        }
    } 
}

void collect(TNode *ph, TPointer *Q){
    TNode *p;
    int i;
    //ph为头结点,最终可以传出去
    
    for(i = 0; !Q[i].front; i++)
        ;//找出第一个队列中非空结点
    ph->next = Q[i].front;
    p = Q[i].rear;
    i++;
    
    for(; i < N; i++){
        if(Q[i].front){
            p->next = Q[i].front;
            p = Q[i].rear;//注意的是Q[i]内部的结点是连接好的 
        }
    }
    p->next = NULL;
} 

void list_sort(int *R, int n){
    int i;
    TNode *ph, *p;
    TPointer Q[N];
    int m = max(R, n);
    
    ph = create_list(R, n);
    
    for(i = 0; m; i++, m /= N){
        dispatch(ph, Q, i);
        collect(ph, Q);
    }
    for(i = 0, p = ph->next; p; p = p->next){
        R[i] = p->data;
    }
    free(ph);
}

码字不易, 赞赞啊!

欢迎评论交流!