写在前面的话：

本讲主要内容讲了连续性的定义，及其三个衍生的表述方式，函数的几类间断点。

最后一个例题回顾了极限的保号性，是不是又有点生疏了？没关系，回过头再看看。反复研读，用心体会。

如果有错误的地方还请提出来，我会及时纠正。大家一起学习吧~

一、函数的连续性：

• 函数连续定义：设
  在
  的某邻域内有定义，如果当自变量的增量
  趋近于零时，对应的函数增量
  也趋近于零，即
  ，则称函数
  在
  点连续。

注：① 我们把

写成

，这样

就可以写成

；

②根据极限差的运算法则（戳我了解），我们把

变换一下就可以得到

，亦即

,最终可得

③ 当

时，

，注释②中的

又可以写成

所以综合以上①②③三个注解，得出如下三个等价的定义：

1. 设
   在
   的某邻域内有定义，如果当自变量的增量
   趋近于零时，
   ，则函数
   在
   点连续；
2. 设
   在
   的某邻域内有定义，如果当自变量的增量
   趋近于零时，
   ，则函数
   在
   点连续；
3. 设
   在
   的某邻域内有定义，如果当自变量的增量
   趋近于零时，
   ，则函数
   在
   点连续。

更多的情况下，我们一般使用第3个等价定义，我们用

语言来描述第3个等价定义：

设

在

的某邻域内有定义。如果对任意的

，总存在正数

，使当

（

，少了左半边大于

的部分，这样保证了

可以取值为

，即

存在

，对比极限定义，有

，再根据本文第3个等价定义，也就恰好证明了函数

在

点连续。

• 函数的单侧连续概念：

如果函数

左极限

存在且等于

，则称

在

点左连续；如果右极限

存在且等于

，则称

于

点右连续。

注：①函数在一点连续的充要条件是在该点处既左连续又右连续。

② 如果函数

在开区间

内每一点连续，则称

是开区间

上的连续函数，或称

在开区间

上连续；函数

在闭区间

连续，是指

在开区间

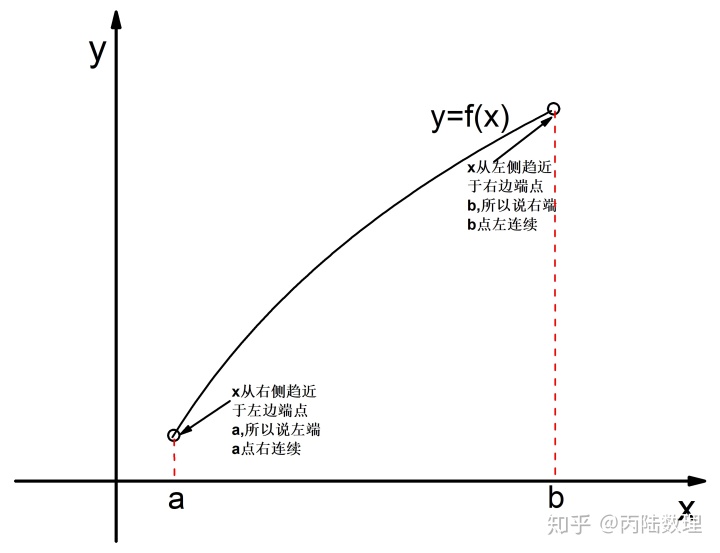
连续，且于左端点

右连续，右端点

左连续。关于左右端点连续的描述如下图所示：

连续函数的例子：

（1）若

是多项式函数，我们前面证明过（戳我了解），对任意的

，有

，亦即多项式函数在任意一点处的极限值都等于该点处的函数值，故多项式函数于

内连续。

（2）若

为有理函数，由前面的证明知（戳我了解），只要

，便有

，因此有理函数在其定义域内是连续的。

（3）函数

在

内连续，下面给出证明：

证明：设

是区间

内任意一点，当

有增量

时，对应函数的增量

，由三角函数和差化积公式（戳我了解）

我们在第七讲重要极限1的证明过程中已经利用单位圆解释过（戳我了解），对于任意角度

,当

时有

，所以

即有不等式

，对此不等式使用夹逼准则（戳我了解）可知，当

时，

，根据函数连续定义知，函数

在

上是连续的。

（4）函数

在

上连续，证明过程与(3)中类似。

二、函数的间断点

设函数

在

的某去心邻域内有定义。如果

有下列三种情形之一：

1.在

处没有定义；

2.虽然在

处有定义，但

不存在；

3.虽然在

处有定义，且

存在 ，但

；

则函数

在

处不连续，称

为

的间断点。

注：实际上，以上三点本质上就是破坏了函数连续定义中

的三种不同情况，破坏了这个等式肯定就不连续了，从而是间断的了。

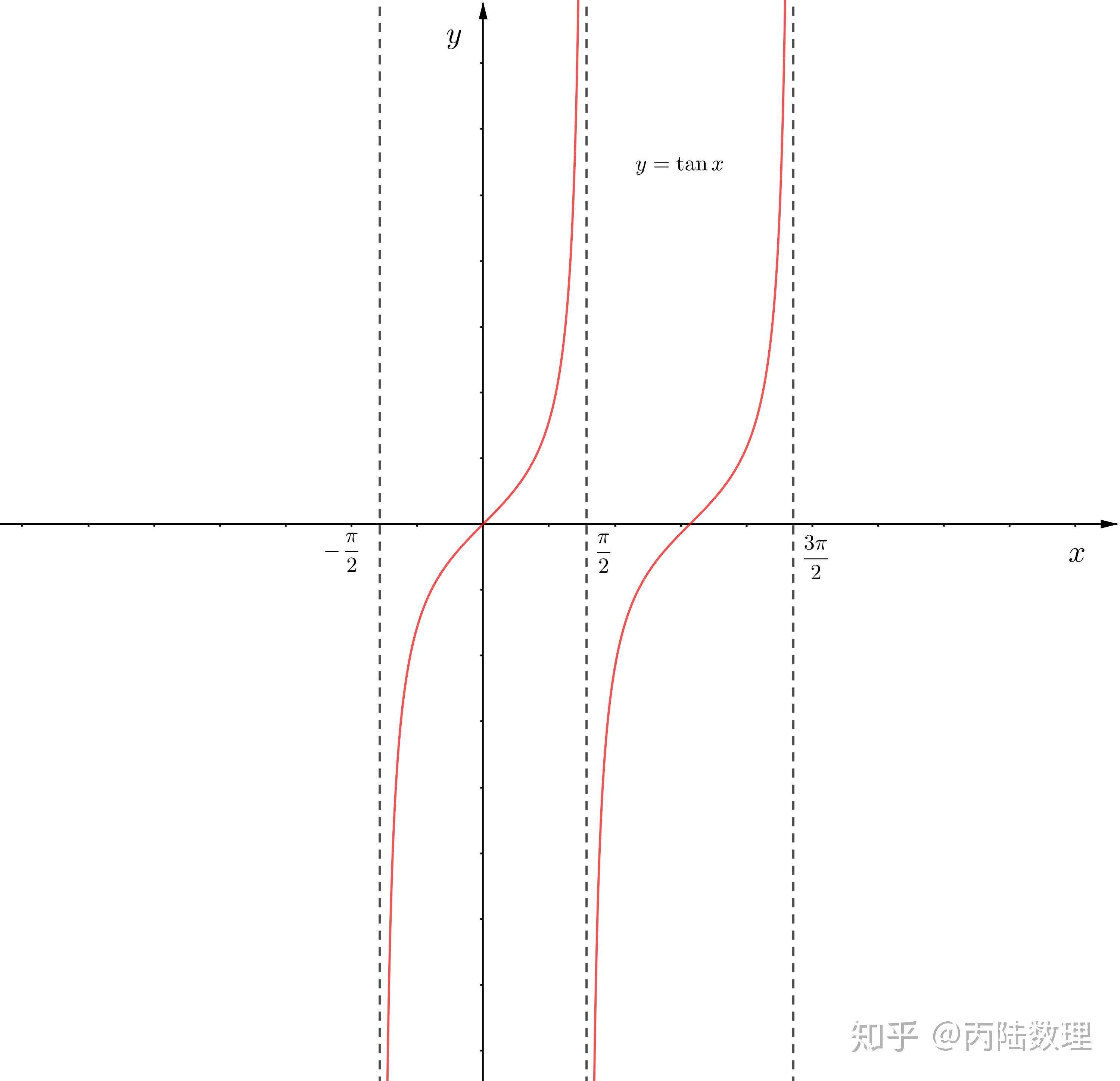
例1.正切函数

在

处没有定义，所以破坏了等式

，故

是

的间断点。又

，故称

为

的

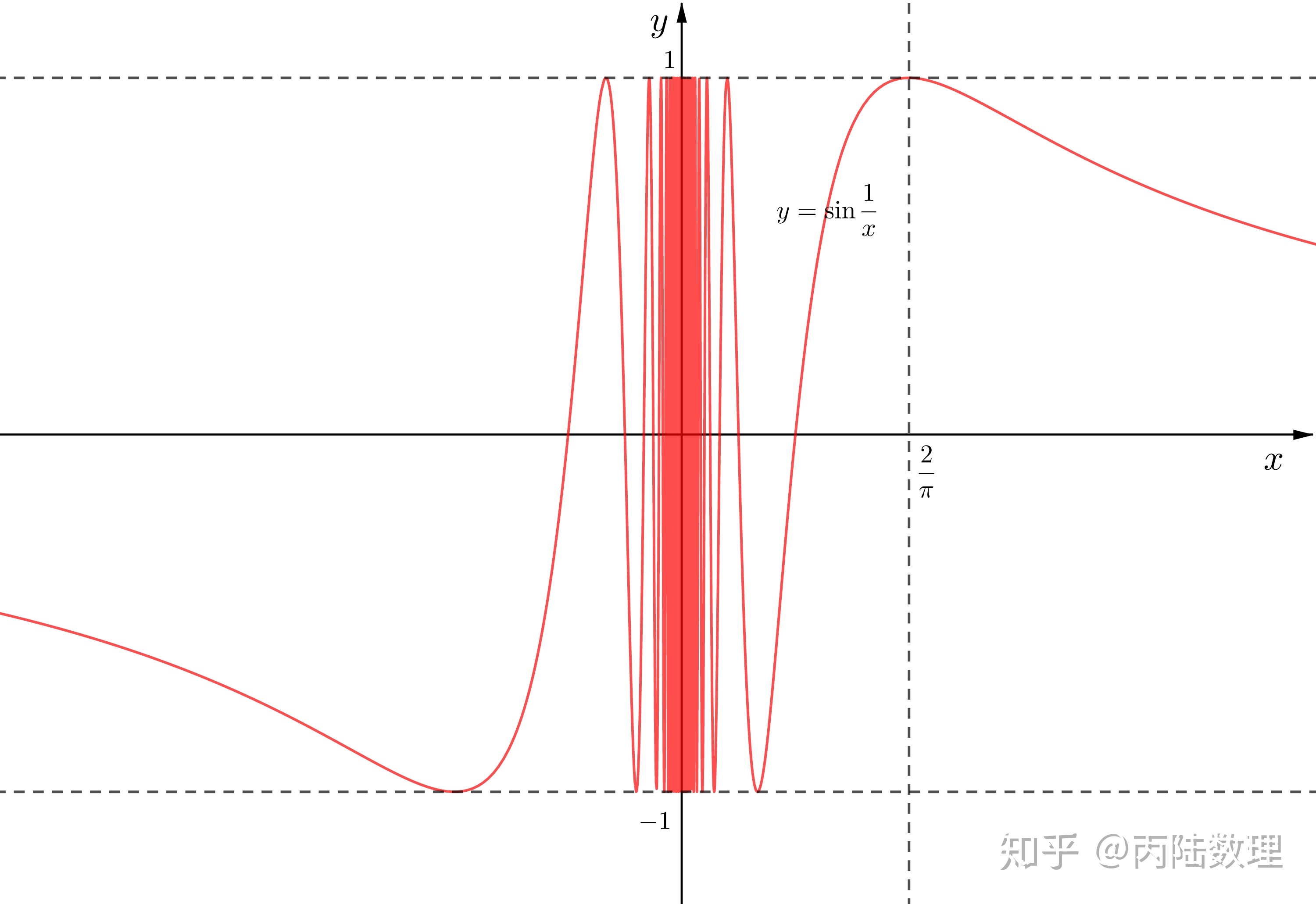
例2.函数

在点

处没有定义，当

时，

，函数值在

和

之间变动无限多次，所以

称为函数

的

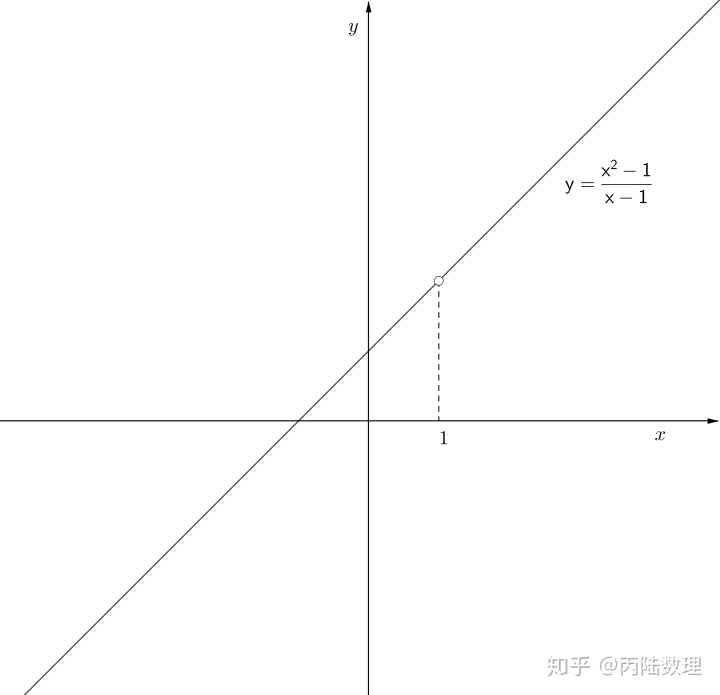
例3.函数

在点

，没有定义，所以函数在

不连续，但

，如果补充点

，则函数在

处就连续了，所以

为该函数的

例4.函数

在

处有定义

，又

，所以

是

的间断点。但如果改变

在

处的函数值：

，则

于

点处连续，所以

是

的

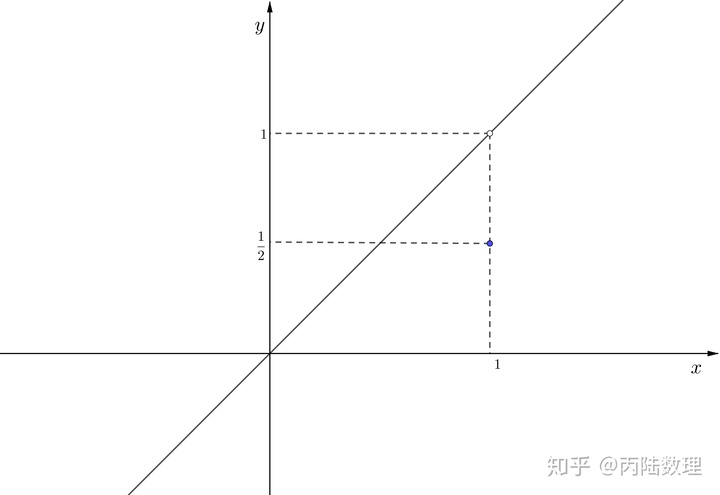
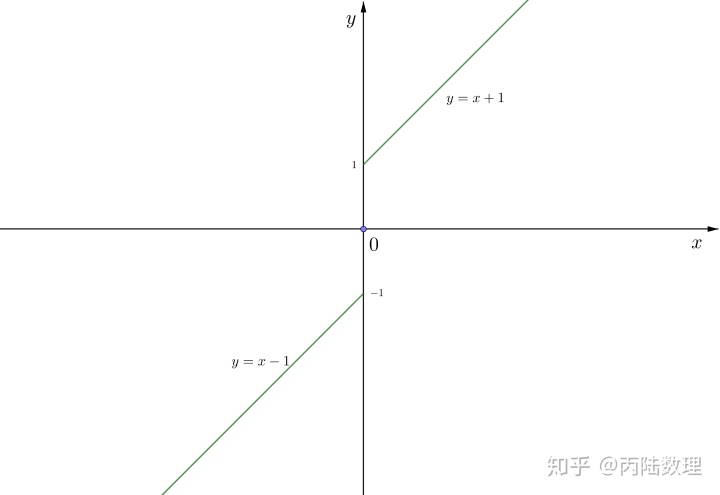
例5.函数

在

处有定义，

，且

，左右极限都存在但是不相等，故

是

的间断点。因为

的图形在

有跳跃现象，故称

是

的

以上我们讨论了无穷间断点、振荡间断点、可去间断点和跳跃间断点。那么我们通常把这些间断点分为两大类：

① 如果

是

的间断点，左极限

与右极限

都存在（不一定相等），则称

为第一类间断点（可去间断点、跳跃间断点）。

②如果

左右极限有一个不存在或两个都不存在，则称

为第二类间断点（无穷间断点、振荡间断点）。

下面再补充一个例题：

例6：证明函数

在点

处连续且

，则存在

的某邻域

，使当

时，

。

证明：由于

于

处连续，所以

，由第七讲中极限的保号性定理之定理1'（戳我了解），存在

的某去心邻域

，使当

时，

，故当

时，

。