题目描述
如果一些边长互不相同的正方形，可以恰好拼出一个更大的正方形，则称其为完美正方形。
历史上，人们花了很久才找到了若干完美正方形。
比如：如下边长的22个正方形
2 3 4 6 7 8 12 13 14 15 16 17 18 21 22 23 24 26 27 28 50 60
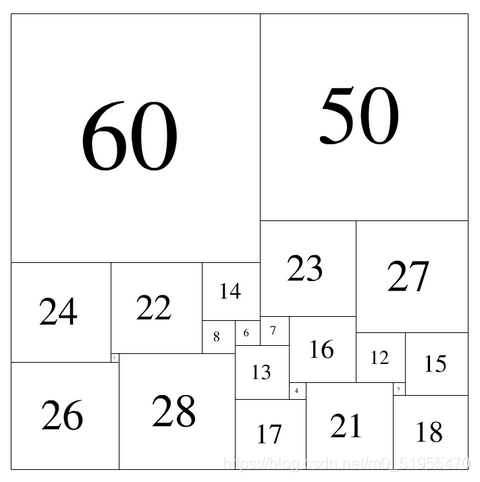
如下图那样组合，就是一种解法。此时，
紧贴上边沿的是：60 50
紧贴下边沿的是：26 28 17 21 18

22阶完美正方形一共有8种。下面的组合是另一种：
2 5 9 11 16 17 19 21 22 24 26 30 31 33 35 36 41 46 47 50 52 61
如果告诉你该方案紧贴着上边沿的是从左到右依次为：47 46 61
你能计算出紧贴着下边沿的是哪几个正方形吗？
输出
请提交紧贴着下边沿的正方形的边长，从左到右，用空格分开。

解题思路：
将完美正方形看成是一个由154*154个单元格组成。以行列为顺序进行遍历，找到未被填充的格子，并以其为起点将小正方形填充至完美正方形中，当剩余的所有小正方形都无法填充，则进行回溯。当所有小正方形都顺利填入，则得到答案。

代码如下：

#include <iostream>
using namespace std;
const int N = 154;
int mp[154][154];int a[] = {2, 5, 9, 11, 16, 17, 19, 21, 22, 24, 26, 30, 31, 33, 35, 36, 41, 50, 52};
bool vis[25];void fill(int x, int y, int n, int num) {for (int i = x; i < x + n; i++)for (int j = y; j < y + n; j++)mp[i][j] = num;
}bool check() {for (int i = 0; i < 154; i++)for (int j = 0; j < 154; j++)if (!mp[i][j])return false;return true;
}bool judge(int x, int y, int n) {if (x + n > 154 || y + n > 154)return false;for (int i = x; i < x + n; i++)for (int j = y; j < y + n; j++)if (mp[i][j])return false;return true;
}bool dfs(int x, int y) {if (check())return true;else {bool flag = true;for (int i = 0; i < 154 && flag; i++)for (int j = 0; j < 154 && flag; j++)if (!mp[i][j]) {x = i, y = j;flag = false;}for (int k = 0; k < 19; k++) {if (judge(x, y, a[k])) { //先判断能不能放，再判断有没有用过if (!vis[k]) {vis[k] = true;fill(x, y, a[k], a[k]);if (dfs(x, y))return true;fill(x, y, a[k], 0);//恢复现场vis[k] = false;}} elsebreak;}}return false;
}int main() {fill(0, 0, 47, 47);fill(0, 47, 46, 46);fill(0, 93, 61, 61);dfs(0, 0);int ans = -1;for (int i = 0; i < 154; i++) {if (mp[153][i] != ans) {cout << mp[153][i] << " ";ans = mp[153][i];}}cout << endl;return 0;
}