python二维散点分布图_深入理解皮尔逊相关系数amp;python代码

1.常见理解误区

（1）计算出变量A和变量B的皮尔逊相关系数为0，不代表A和B之间没有相关性，只能说明A和B之间不存在线性相关关系。

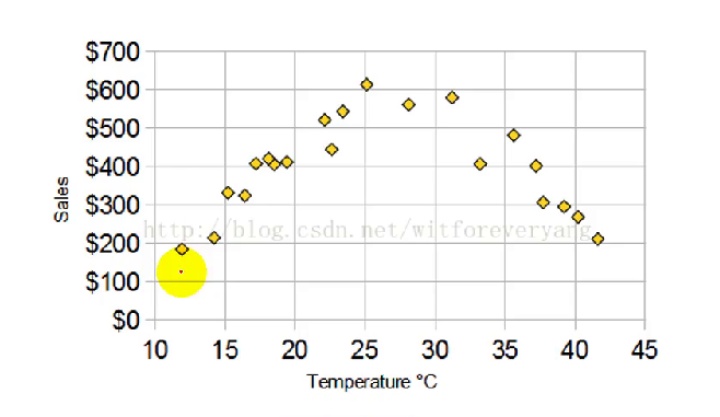
例：温度和冰淇淋销量之间的散点图像如下，可以发现大致成二次函数图像，随着温度升高，销量也会增加，达到峰值后，随着温度升高，销量反而下降。也就是说，销量和温度之间是有关系的。

不过，计算温度和销量之间的皮尔逊相关系数却为0。这只能说明温度和销量之间没有线性相关关系，而不能说二者不存在相关关系。

图片来自于网络博客

（2）皮尔逊相关系数并不稳定，会受到异常点的影响。

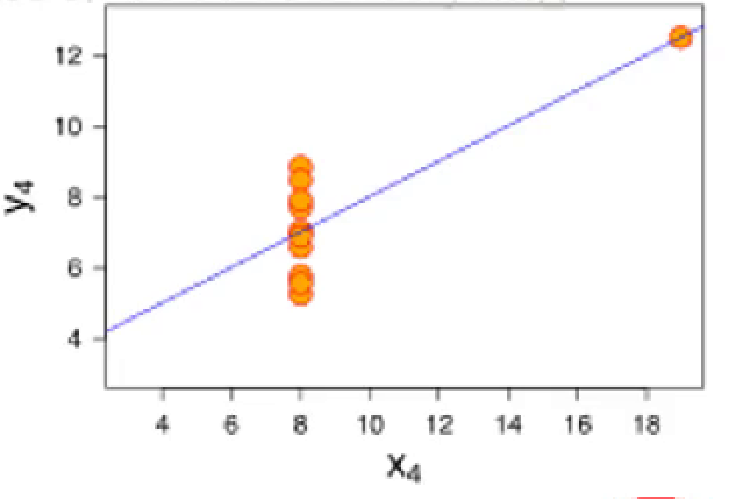
例：如果不考虑最右侧的异常点，x和y之间的相关系数应该为0，即无论y取何值，x都为固定值8。但是，考虑了异常点后，x和y的相关系数变为0.816。

这也说明，在进行数据分析之前，需要对数据进行清洗，去掉异常点、噪声数据，使得分析结果更为可靠。

（3）皮尔逊相关系数绝对值越大，二者相关性越强？

答案是不一定。除了相关系数的大小，我们更要关心相关系数的显著性。

2.皮尔逊相关系数正确使用步骤

第一步：绘制散点图，是否存在异常点。如果有异常点，删除异常点。然后再看观察变量x和变量y之间的关系是否近似为一条直线，如果是，则计算皮尔逊相关系数。相关系数为(0,1]的正数，表明x和y之间呈线性正相关；相关系数为0，表明二者不存在线性相关关系，但不排除存在其他非线性相关关系；相关系数为[-1,0)的负数，表明x和y之间存在线性负相关关系。

如果散点图并不类似于一条直线，而是其他类型图像，如二次函数图像、指数图像，即使计算出皮尔逊相关系数也没有意义。

3.python代码示例

python sklearn库中datasets模块中有一个boston房价数据集，可以使用load_boston()函数进行加载。

print(load_boston().DESCR)#查看boston数据集基本信息

#加载数据集并进行数据处理
from sklearn.datasets import load_boston
import pandas as pd
rawdata = load_boston()#加载数据
features = pd.DataFrame(rawdata.data,columns = rawdata.feature_names)#提取特征集
label = pd.DataFrame(rawdata.target,columns = ['target'])#提取标签列boston = pd.concat([features,label],axis =1)#合并特征集和标签列
print(boston)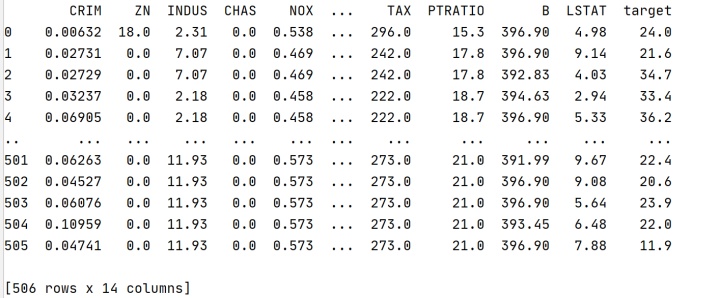

#绘制散点矩阵图，由于boston矩阵共有14个属性，全部属性两两绘制散点图过于庞大，因此选择其中3个属性进行两两组合绘制散点图
import matplotlib.pyplot as plt
import seaborn as sb
sb.pairplot(data = boston,vars = ['CRIM','INDUS','target'])#'CRIM','INDUS','target'三个变量之间两两组合绘制散点图
plt.savefig('C:UsersCaraDesktopscatter fig.png')#绘图结果存到本地

绘图如下：

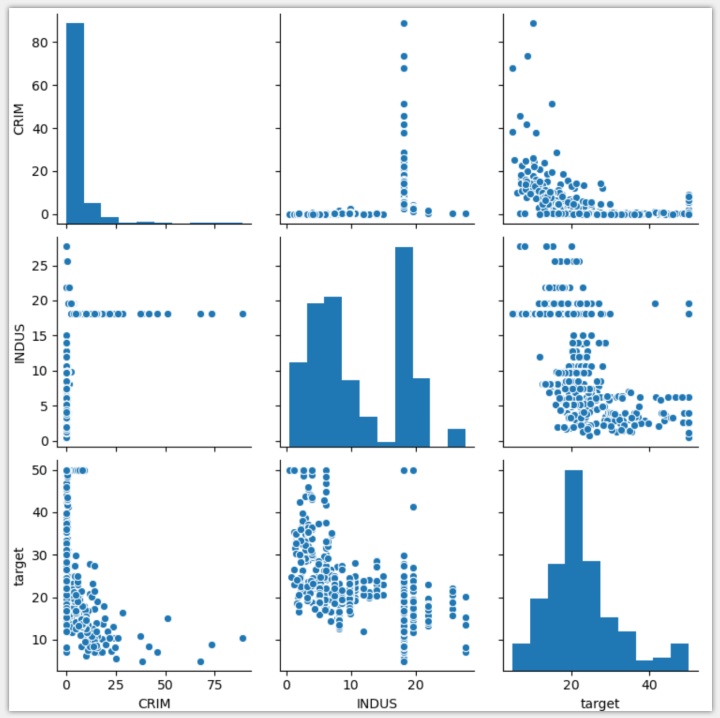
3个变量，两两组合绘制出6幅散点图，其中有3幅会是重复的，我们只需要看左下角3幅，或右上角3幅即可。

蓝色柱形图是变量的数值频率分布图。

从散点图可以看出，CRIM和INDUS并没有线性相关性。

CRIM和target（房价）大致成负相关性，图像接近指数函数（非线性函数），因此，计算出的相关系数可能并不可靠。

INDUS和target之间大致成负线性相关，同时右侧存在几个异常点，最终计算出的相关系数会受到异常点的影响。

直观的认识需要精确的相关系数作为检验：

注释：corr()方法默认的相关系数为皮尔逊，也可以设置method 参数为其他类型的相关系数，如 'kendall', 'spearman'。

由于宽度限制，中间列显示不完全，可以设置参数：

#更改显示设置，打印全部列
pd.set_option('display.max_columns',None)#若单行不够显示全部列，将会换行显示
print(boston.corr())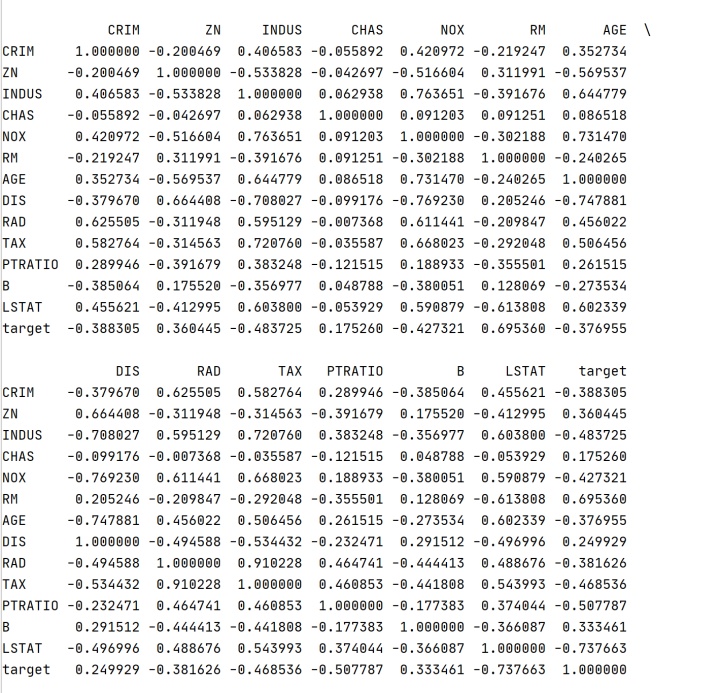

查看单个变量与其他变量间的皮尔逊相关系数：

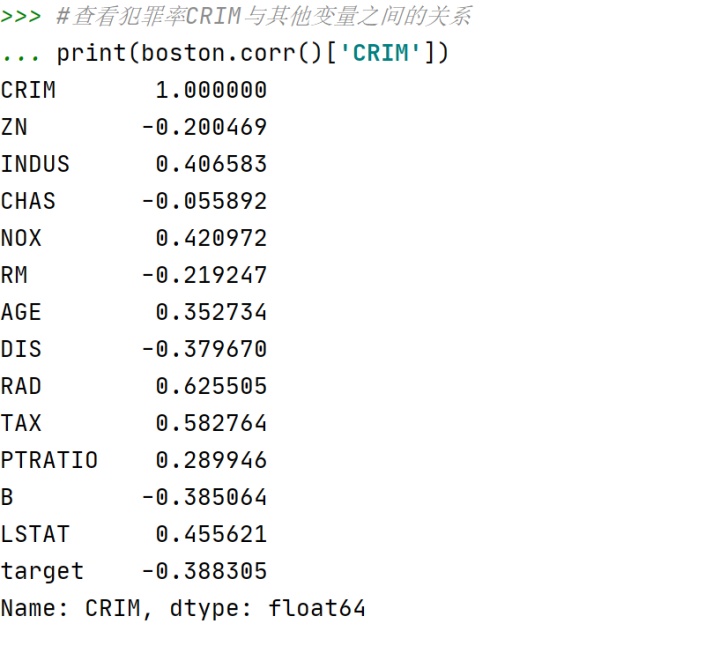
由上可见，犯罪率确实与房价呈负相关。不过，没有显著性指标作为支持。

如果需要同时返回皮尔逊相关系数和显著性指标，则可以使用scipy库中stats模块中的stats模块下的pearsonr 函数。stats是一系列统计方法的集合，如峰度、t检验、相关性、F检验……

from scipy.stats import stats
help(stats.pearsonr)

#使用scipy中的函数计算相关系数及显著性
from scipy.stats import stats
r,p_value = stats.pearsonr(boston['CRIM'],boston['target'])#计算CRIM和target之间的相关系数和对应的显著性
print('相关系数为{:.3f},p值为{:.5f}'.format(r,p_value))#相关系数保留3位小数，p值保留5位小数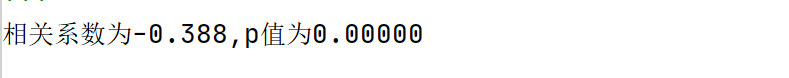

p值远小于0.01，表明CRIM和target 在1%的水平上存在显著的线性相关，对应的相关系数为-0.388。

不过，使用这种方法缺点很明显，不能一次性计算所有变量两两组合的相关性。

最后，绘制热力图，直观展示变量间的线性相关性：

#绘制相关系数的热力图
import seaborn as sb
r_pearson = boston.corr()
sb.heatmap(data = r_pearson)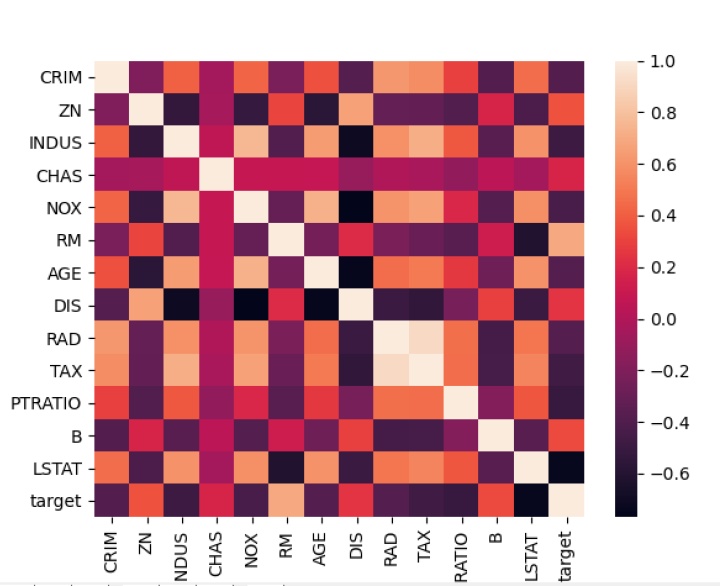

换个色系：

sb.heatmap(data = r_pearson,cmap="YlGnBu")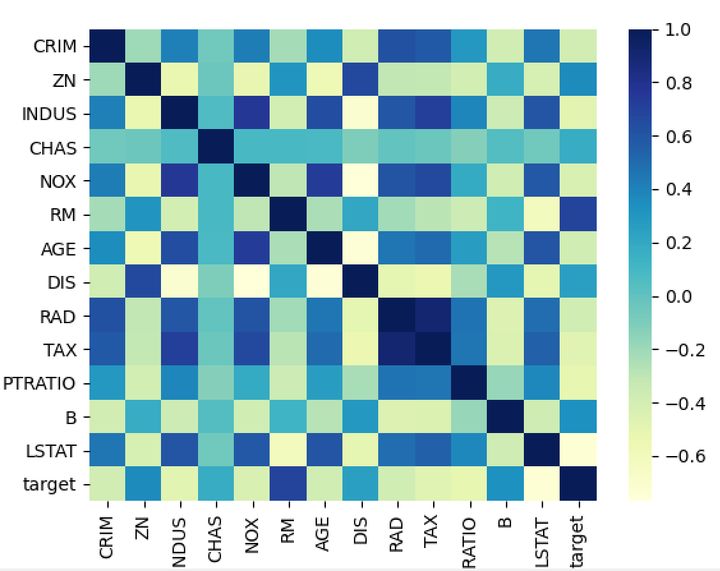

全部代码如下：

from sklearn.datasets import load_boston
import pandas as pd
#查看Boston数据集的基本信息
print(load_boston().DESCR)rawdata = load_boston()#加载数据集
features = pd.DataFrame(rawdata.data,columns = rawdata.feature_names)#提取特征列
label = pd.DataFrame(rawdata.target,columns = ['target'])#提取房价列（target列）
boston = pd.concat([features,label],axis =1)#组合特征列和房价列#绘制散点图
import matplotlib.pyplot as plt
import seaborn as sb
sb.pairplot(data = boston,vars = ['CRIM','INDUS','target'])
plt.savefig('C:UsersCaraDesktopscatter fig.png')#计算全部变量的相关性矩阵
print(boston.corr())#查看目标变量‘房价’与其他变量间的相关性
print(boston.corr()['target'])#查看犯罪率CRIM与其他变量之间的关系
print(boston.corr()['CRIM'])#更改显示设置，打印全部列
pd.set_option('display.max_columns',None)
print(boston.corr())#使用scipy中的函数计算CRIM和target的相关系数及显著性
from scipy.stats import stats
r,p_value = stats.pearsonr(boston['CRIM'],boston['target'])
print('相关系数为{:.3f},p值为{:.5f}'.format(r,p_value))#绘制相关系数的热力图
import seaborn as sb
r_pearson = boston.corr()
sb.heatmap(data = r_pearson,cmap="YlGnBu")#cmap设置色系

参考：

【强烈推荐】清风：数学建模算法、编程和写作培训的视频课程以及Matlab等软件教学_哔哩哔哩 (゜-゜)つロ干杯~-bilibiliwww.bilibili.com