图论若干定义

• 图（graph）G=（V,E）由定点vertex的集合V， 和边edge的集合E组成。每一条边都是一个点对点（v，w），其中 v,w 属于V集合的子集

• 如果点对点 是有序的，那么图就是有向图（directed）

• 图中的一条路径Path是定点序列的集合 w1，w2，w3，…wn使得（w（i）， w（i+1）） 是边E的子集 其中（1<= i <= N）,这样一条路径的长度（length）是该路径上的边数，他等于N-1。从一个点的到他自身可以看成是一条路径，如果路径不包含边，那么路径的长度为0.

• 如果图有一条从一个定点到自身的边（v，v），那么这条路径v，也叫作环（loop）

• 连通图

  • 如果一个无向图中从一个顶点到每个其他顶点存在一条路径，则称改无向图是连通图

• 强连通图

  • 一个有向的连通图是强连通图

• 基础图

  • 如果一个有向图不是强连通图，但是他的有基础的图结构，即其边上去掉方向所成的图是连通的，那么改有向图称为弱连通图

• 完全图

  • 若图中每一对顶点之间都存在一条边的，我们称这种图为完全图

• 现实中案例

  • 航空系统，每个机场都是顶点，机场之间的航线是边，边可以有权重标识时间，距离费用等。
  • 交通流可以用一个图来模型化，每一条街道交叉口标识一个顶点，每一条街道都是一条边。边的值可以代表速度限制，或者容量（车道数量）等。我们可以找一条最短路径或者用改信息找出交通瓶颈最可能的位置。

图的表示（基本数据结构）

• 我们先用一个案例有向图（无向图类似表示）如图中假设可以从1号顶点编号。图中不表示7个顶点和12条表。
  

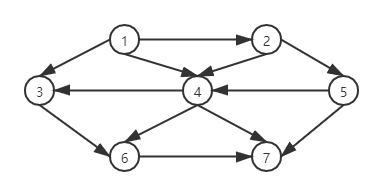
方法一二维数组

• 最简单的数据结构使用一个二维数组标识，称为邻接矩阵（adjacent matrix） 标识法。对于每条边（u，v），设置A[u][v] = true;否则 设置false。如果边有一个权重，那么我们设置A[u][v] = X权重值。例如，我们寻找最廉价的航空线路，那么我们可以用 MXA 无穷大标识不存在航线。如果处于某种原因我们找到最昂贵的路线，那么可以用 -MAX表示不存在的边。
• 以上二维数组的表示方式优点是非常简单，但是空间需求是O（V^2）， 如果图的边不是很多，那么这种标识的代价就会非常大，若图是稠密（dense）的：E = O(| V ^ 2|)，那么我们用二维数组的邻接矩阵的标识方法是合适的，因为数据结构中每一个位置的值都是有用的值。
• 致命的缺点在于我们现实生活中的案例几乎都是稀疏的数据，例如街道路口，几乎所有街道多的话都只有四个方向东南西北，因此任意路口的标识为节点， 方向标识边，那么E = 4V，如果3000 个路口，3000 个顶点，12000 条边，那么需要3000*3000 的数组，而且数组中大部分元素都是false，因为一个节点只连接附近四个节点，与其他节点的连通数据位false。浪资源

方法二邻接表

• 如果图不是稠密的，是稀疏的，则更好的解决方案就是邻接表（adjacency list）表示，对每一个顶点，我们使用一个表存放所有邻接的顶点。这个时候占用的空间是 O(E+ V)，他相对于图的大小而言是线性的，这种抽象表示方法我们用如下图表示，很想一个MAP数据接口的样子。如果边有权重，那么我们可以在图节点E中附加信息增加权重信息，存在邻接表中。
  

• 邻接表是标识图的标准方法。无向图可以类似的标表示，每条边（u，v）出现在两个表中，因此空间的使用基本是双倍的。在图论算法中通常需要找出与某个给定顶点v邻接的所有的顶点。 而这可以通过简单的扫描相应邻接表来完成，用时与这些找到顶点的个数成正比

• 如下代码定义邻接表节点：

/*** 图节点元素* @author liaojiamin* @Date:Created in 16:28 2020/12/28*/
public class Vertex implements Comparable<Vertex> {//图节点出度节点 数组private List<Vertex> vertexList = new ArrayList<>();//图节点入度节点 数组private List<Vertex> insertVertexList = new ArrayList<>();private Integer dist;private boolean know;//目标节点到本节点的上一个节点的 节点信息private Vertex path;private Integer weight;public List<Vertex> getInsertVertexList() {return insertVertexList;}public void setInsertVertexList(List<Vertex> insertVertexList) {this.insertVertexList = insertVertexList;}public Integer getWeight() {return weight;}public void setWeight(Integer weight) {this.weight = weight;}public Vertex getPath() {return path;}public void setPath(Vertex path) {this.path = path;}public List<Vertex> getVertexList() {return vertexList;}public void setVertexList(List<Vertex> vertexList) {this.vertexList = vertexList;}public Integer getDist() {return dist;}public void setDist(Integer dist) {this.dist = dist;}public boolean isKnow() {return know;}public void setKnow(boolean know) {this.know = know;}@Overridepublic int compareTo(Vertex o) {return this.dist - o.dist;}
}

拓扑排序

• 拓扑排序是对有向无圈图的顶点的一种排序，是的如果存在一条从Vi 到Vj的路径，那么在排序中Vj就出现在Vi的后面，如下图中，有向边（v，w）表示在v必须先比w 先完成。如果图中含有圈，那么拓扑排序是不可能存在的，因为对圈上的任何两个顶点v，w，v先于w同时也需要满足w先于v。此处拓扑排序不必是惟一的；任何合理的排序都是合理的。如下图所示：
  
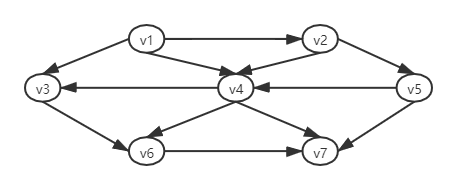
• 图中v1,v2,v5,v4,v3,v6,v7和v1,v2,v5,v4,v7 两个都是拓扑排序

拓扑排序算法分析

• 一个简单的拓扑排序算法
  • 先找出任意一个没有入边的顶点
  • 显示出改顶点
  • 将他及其边一起从图中删除
  • 对图中其余部分同样用这种方法处理。
• 实现方式如下：

/*** 图论 求拓扑排序算法* @author liaojiamin* @Date:Created in 14:56 2021/1/6*/
public class GraphTopLogicalSort {//节点定义：Vertex//图节点相邻节点组//    private List<Vertex> vertexList = new ArrayList<>();  存储节点出度节点//    private List<Vertex> insertVertexList = new ArrayList<>(); 存储节点入度节点//    private Integer dist; 存储节点拓扑编号//假设图基本数据结构已经被读入邻接表中private static final List<Vertex> vertices = new ArrayList<>();/*** 寻找入度为0 的图节点* */public Vertex findNewVertexOfIndegreeZero(){Vertex insetZeroVertex = null;for (Vertex vertex : vertices) {if(vertex.getInsertVertexList().size() <= 0){insetZeroVertex =  vertex;}}//节点入度，出度都为0 ，删除节点信息if(insetZeroVertex != null && insetZeroVertex.getVertexList().size() <= 0){vertices.remove(insetZeroVertex);}return insetZeroVertex;}/*** 拓扑排序算法* */public void topSort(){for (int i = 0; i < vertices.size(); i++) {Vertex v = findNewVertexOfIndegreeZero();if(v == null){//每个节点都有入度，说明是有圈return;}v.setDist(i);for (Vertex vertex : v.getVertexList()) {//更新V节点相邻节点中所有信息vertex.getVertexList().remove(v);}}}
}

• 以上实现方式中，findNewVertexOfIndegreeZero方法是对顶点数组的一个遍历，所有每次对他的调用都会花费O(V)的世界，由于有V次这样的调用，所有算法时间复杂度为O(V^2)
• 优化方式：邻接表标识图的方式注定他是稀疏的，因此我们每次去更新节点的入度的时候只有少部分节点需要更新，也久只有少部分节点的入度将变为0 ，此时我们通过扫描所有数据的方式来查找入度为 0 的代价太大
• 我们可以用一个队列或者栈来存储入度为 0 的节点，对每个顶点计算入度后然后将入度为0 的节点天界到队列，当队列不为空，就删除顶点V并将对应邻接节点入度减去v，这样拓扑排序的顺序就是出队列的顺序。
• 代码实现如下：

  /*** 优化拓扑算法* */public void topSort_v1(){List<Vertex> insertZeroVertex = new ArrayList<>();insertZeroVertex.add(findNewVertexOfIndegreeZero());int i = 0;while (insertZeroVertex.size() > 0){Vertex v = insertZeroVertex.remove(0);v.setDist(i++);for (Vertex vertex : v.getVertexList()) {//减少入度vertex.getInsertVertexList().remove(v);if(vertex.getInsertVertexList().size() <= 0){//将入度为0 的节点加入队列insertZeroVertex.add(vertex);}}}}

最短路径算法

• 最短路径算法是在赋权图的情况下使用：与每条边（vi，vj）想联系的是穿越改边的代价（权重）Cij。一条路径v1v2v3v4…vn的值叫做赋权路径长度（weighted path length），而无权路径长（unweighted path length）只是路径上边的数量，即N-1。

单源最短路径问题

• 给定一个赋权图G= （V，E）和一个特定顶点s作为输入，找出s到G中每一个其他顶点的最短赋权路径。如下案例
  

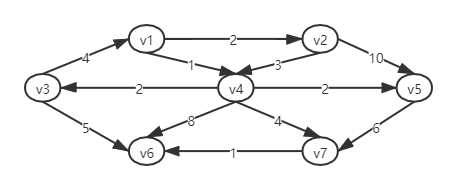
• 从v1到v6的最短赋权路径的值为6，他是从v1 到 v4 到v7 在到v6的路径。在这两个顶点之间的最短无权路径长度为2.一般说，当不指名我们讨论的是赋权路径还是无权路径时候，如果图是赋权的那就是赋权路径。还有上图中从v6 到v1 是无路径的。

负圈值

• 以上案例中，如果存在负数的权重那么会有问题如下图。从v5 到v4 的路径值为1，但是通过下面的循环v5,v4,v2,v5,v4存在一条更短的路径，他的值是-5.这条路径任然不是最短的，因为我们可以循环中不断的重复。因此这两个顶点之间最短路径问题是不确定的。类似v1， 到v6的最短路径也是不确定的。这种情况就叫做负圈值
• 当图中存在负圈值，最短路径问题是不确定的，有负的边增加问题难度
  

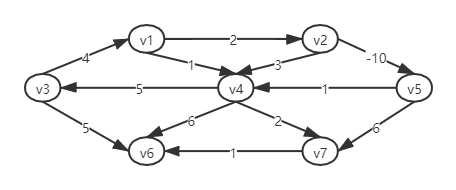
四种最短路径目标

• 首先开了无权最短路径问题并指出如何以O(E+V)的时间复杂度求解
• 无负边情况先求解赋权最短路径，使用合理数据结构实现运行时间在O(ElogV)
• 有负边情况，提供解决方案，时间复杂度O(E*V)
• 以线性时间解决无圈图特殊情况的赋权问题

无权最短路径

• 如下图表示一个无权图G，使用某个顶点s作为输入参数我们要找出从s到所有其他顶点的最短路径。因为是无权所有我们只需要关注边，我们将他当成是权重为1 的赋权问题。

1. 算法分析

• 选择s为v3，次数立刻可以看出s到v3的最短路径是0 ，到自己接的是无距离的。标记如图
  
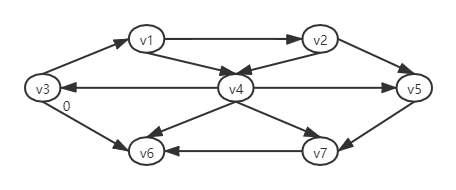
• 接着寻址与s相邻的节点，即s出发距离为1 的节点。这些顶点可以通过查询与s节点的领接节点数组来找到。我们看到v1和v6与s相邻，如下图：
  
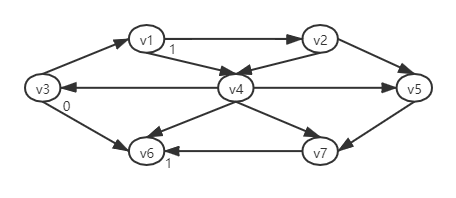
• 同理继续寻址邻接到v1和v6的顶点，显然是v2，v4，他们到v3的最短路径是2：

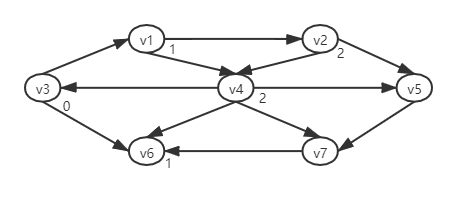
• 最后通过v2，v4的邻接节点找到v5，v7各有一条3的最短路径:

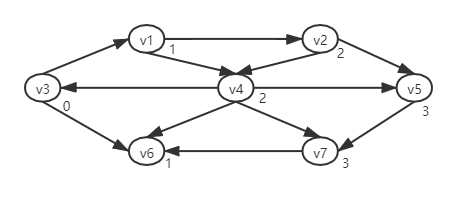
• 以上搜索图的方法称为广度优先搜索（breadth-first search）。按层处理顶点：距离开始最近的那些顶点首先被求值，最远的顶点最后被求值。这很像树的层序遍历（level-order traversal）。

• 算法分析

  • 对每个顶点跟踪三个信息，首先将从s开始到顶点的距离dist记录为0，因为s到自身的距离是0
  • 顶点s的path属性记录为null这个变量用来标记我们能够显示出的实际路径
  • know变量标记为false，标识他是否被处理过，处理过后标记为true，保证不会重复处理而导致更长的路径，因为按广度优先原则，首先处理的路径一定是对短的路径。
  • 算法流程将dist = 0 上的顶点声明为know，接着，dist = 1 上的顶点声明为know，在dist = 2的know，依次类推，并且每一步骤将上一步骤节点存储在Path中
  • 我们通过追溯Path遍历，可以显示实际的路径：如下代码实现：

/*** 最短路径算法* @author liaojiamin* @Date:Created in 16:29 2020/12/28*/
public class GraphShotLine {//图节点数组private static final List<Vertex> vertexVraph = new ArrayList<>();private static final Integer MAX_DIST = Integer.MAX_VALUE;/*** 递归打印路径* */public void printPath(Vertex v){if(v.getPath() != null){printPath(v.getPath());}System.out.println(v);}/*** 无权重图最短路径算法 解法一* 时间复杂度O(V^2)* */public void unweighted(Vertex s){for (Vertex vertex : vertexVraph) {vertex.setDist(MAX_DIST);vertex.setKnow(false);}s.setDist(0);Integer NUM_VERTICES = vertexVraph.size();//遍历从 0 ~ MAX 距离的距离范围内所有节点到目标节点的距离，默认最差是链式，距离是NUM_VERTICESfor (Integer i = 0; i < NUM_VERTICES; i++) {for (Vertex vertex : vertexVraph) {if(!vertex.isKnow() && vertex.getDist() == i){vertex.setKnow(true);for (Vertex sunVertex : vertex.getVertexList()) {if(sunVertex.getDist() == MAX_DIST){sunVertex.setDist(i + 1);sunVertex.setPath(vertex);}}}}}}}

• 如上代码实现中双重for循环，时间复杂度O(v^2).一个明显的效率低下的地方在于，在for循环还未结束的时候，其实已经将所有节点都已经编辑为know，但是循环还在继续。直到所有节点都被遍历一次为止。
• 优化方式，我们可以用类似对拓扑排序的做法来避免这种双重循环，最简单的方式我们将即将要处理的节点放入队列中，然后依次从队列中取出来处理：
  • 当处理s节点的时候，将s设置know，将s添加到有序队列
  • 将出队列第一个节点，此时是s节点，将s邻接节点的dist+1，并且将所有邻接节点如队列
  • 持续上面两个步骤，知道队列中的节点为空为止
  • 如下代码实现：

/*** 最短路径算法二* @author liaojiamin* @Date:Created in 16:29 2020/12/28*/
public class GraphShotLine {//图节点数组private static final List<Vertex> vertexVraph = new ArrayList<>();private static final Integer MAX_DIST = Integer.MAX_VALUE;/*** 递归打印路径* */public void printPath(Vertex v){if(v.getPath() != null){printPath(v.getPath());}System.out.println(v);}/*** 无权重图最短路径算法 解法二* */public void unweighted_1(Vertex s){for (Vertex vertex : vertexVraph) {vertex.setDist(MAX_DIST);vertex.setKnow(false);}s.setDist(0);LinkedList<Vertex> sunVertexList = new LinkedList<>();sunVertexList.addFirst(s);while (!sunVertexList.isEmpty()){Vertex sunVertex = sunVertexList.getFirst();sunVertexList.removeFirst();for (Vertex vertex : sunVertex.getVertexList()) {if(vertex.getDist() == MAX_DIST){vertex.setDist(sunVertex.getDist() +1);vertex.setPath(sunVertex);sunVertexList.addLast(vertex);}}}}
}

• 使用拓扑排序的方式处理最短路径问题，只要使用的是邻接表运行时间就是O(E+V)

Dijkstra算法

• 如果图是有权重图，那么问题会更复杂一点，但是算法还是可以通用。我们还是保留之前的图节点结构。
• 解决单源最短路径问题一般嘴阀叫做Dijkstra算法（Dijkstra`s algorithm）。这个有很多年历史的解决方法是贪婪算法（greedy algorithm）最好的案例。贪婪算法一般是分阶段求解一个问题，在每个节点他都把出现的当作是最好的方法。
• Dijkstra算法按阶段进行，和无权最短路径算法一样。每个阶段Dijkstra算法选择一个顶点v，他在所有unknow顶点中具有最小的dist，同时算法声明从s到v的最短路径是known的。阶段的其余部分由dith的更新工作组成。
  • 在无权的情况下，如果dist_w = +Max（无穷大） 那么设置dist_w = dist_v + 1。因此如果顶点v能提供一条更短的路径，则我们本质上降低了dist_w的值。
  • 如果我们对赋权的情况也用这个逻辑，那么当dist_w的新值dist_v+ C_vw，是一个更小的值，那么我们就设置dist_w = dist_v + V_vw
  • 总的来说使用通过w节点的路径上的顶点v是不是一个最优解取决于算法，原始的dist_w 是不使用v的值的，以上所有算出的值是使用v值后的最短路径

算法分析

• 依然按照之前的案例，如下图中，设开始节点s是v1，第一个选择的顶点是v1，路径长度 0 ，标记v1为known，即v1是known的，那么其他的节点的dist值就需要调整，邻接到v1的节点v2， v4 两个调整
  
• v2， v4 跳转之后的节点情况如下表格所示

v	knwn	dist	path
v1	T	0	null
v2	F	2	v1
v3	F	MAX	null
v4	F	1	v1
v5	F	MAX	null
v6	F	MAX	null
v7	F	MAX	null

• 下一步选取v4， 因为v4.dist < v2.dist，标记v3的known = true， 顶点v3， v5，v6，v7,是邻接顶点，他们的实际值需要调整，如下图所示：

v	knwn	dist	path
v1	T	0	null
v2	F	2	v1
v3	F	3	v4
v4	T	1	v1
v5	F	3	v4
v6	F	9	v4
v7	F	5	v4

• 接着选取v2， 只有v4 ，v5是他邻接的顶点，但是v4已经是known我们不做处理，v5 邻接节点我们继续刚才那个步骤 ，那么dist = v2.dist + V_25 = 2+10 =12,显然12 >3 ，因为v5 的最短路径现有的是3 所以，12 不是最优解，v5 保留现在的值不变。

v	knwn	dist	path
v1	T	0	null
v2	T	2	v1
v3	F	3	v4
v4	T	1	v1
v5	F	3	v4
v6	F	9	v4
v7	F	5	v4

• 下一个被选取的是v5，因为v5 是剩下unknown节点中dist最小的一个，那么v7 是他的邻接节点，同样算法，v7 = 3+6 >5，所有保留原来最优值，5 不变，接着v3，还是应为他是dist最小值，v3邻接节点v6 ，dist = 3+5 = 8 < 9，将v6 的dist下调到8 ，最后结果如下图：

v	knwn	dist	path
v1	T	0	null
v2	T	2	v1
v3	T	3	v4
v4	T	1	v1
v5	T	3	v4
v6	F	8	v3
v7	F	5	v4

• 接着继续选v7 ，邻接节点v6 下调到5+1 =6，得到如下：

v	knwn	dist	path
v1	T	0	null
v2	T	2	v1
v3	T	3	v4
v4	T	1	v1
v5	T	3	v4
v6	F	6	v7
v7	T	5	v4

• 最后选v6，

v	knwn	dist	path
v1	T	0	null
v2	T	2	v1
v3	T	3	v4
v4	T	1	v1
v5	T	3	v4
v6	T	6	v7
v7	T	5	v4

• 依据以上算法分析我们可以从某个顶点v开始到某顶点w的实际路径，可以编写一个递归案例跟踪Path变量的值来得到最短路径，如下代码实现：

/*** 最短路径算法* @author liaojiamin* @Date:Created in 16:29 2020/12/28*/
public class GraphShotLine {//图节点数组private static final List<Vertex> vertexVraph = new ArrayList<>();private static final Integer MAX_DIST = Integer.MAX_VALUE;/*** 递归打印路径* */public void printPath(Vertex v){if(v.getPath() != null){printPath(v.getPath());}System.out.println(v);}/*** 有权重图最短路径算法* */public void dijkstra(Vertex s){for (Vertex vertex : vertexVraph) {vertex.setDist(MAX_DIST);vertex.setKnow(false);}s.setDist(0);LinkedList<Vertex> sunVertexList = new LinkedList<>();sunVertexList.addFirst(s);while (sunVertexList.size() > 0){//每次取第一个最小值Vertex smallVertex = sunVertexList.removeFirst();smallVertex.setKnow(true);//保存需要添加的新节点LinkedList<Vertex> newVertexList = new LinkedList<>();for (Vertex vertex : smallVertex.getVertexList()) {if(!vertex.isKnow()){Integer cvw = vertex.getWeight();if(smallVertex.getDist() + cvw < vertex.getDist()){vertex.setDist(smallVertex.getDist() + cvw);vertex.setPath(smallVertex);//处理过的节点才是之后可能的路径newVertexList.add(vertex);}}}//将可能的路径按从小到大顺序加入有序队列sunVertexList.addAll(getSortVertex(newVertexList));}}/*** 对子节点列表进行从小到大排序* */public LinkedList<Vertex> getSortVertex(List<Vertex> vertexs){if(vertexs.size() <= 0){return null;}for (int i = 0; i < vertexs.size(); i++) {for(int j = i;j > 0;j--){if(vertexs.get(j-1).compareTo(vertexs.get(j)) > 0 ){Vertex vertex = vertexs.get(j-1);vertexs.set(j-1, vertexs.get(j));vertexs.set(j, vertex);}}}return new LinkedList<>(vertexs);}}

• 如上算法中，每次节点w的举报变化时候，将w和新值d_w插入到队列中，这样对优先队列中的每个顶点就可能有多个对象在队列中，当我们deletedMin（出队列首元素）操作将最小的顶点从队列中删除，必须坚持是否是known，如果是就忽略不处理，接着执行下一次deleteMin。
• 算法的队列最大可能达到E （所有节点集合）这么多。由于E<=V^2，那么logE <= 2logv，因此并不影响时间界限

上一篇：数据结构与算法–B树原理及实现
下一篇：数据结构与算法–图论-最短路径算法应用