数据结构与算法--解决问题的方法-顺时针打印矩阵

顺时针打印矩阵

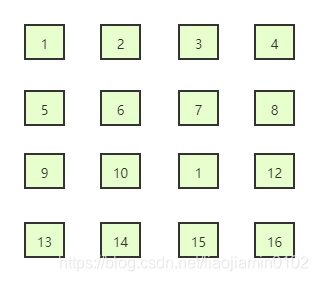
题目输入一个矩阵，按照从外向里顺时针的顺序依次打印每一个数字。例如下案例：
如上图矩阵，顺时针打印：1,2,3,4,8,12,16,15,14,13,9,5,6,7,1,10
以上问题看起来比较复杂，但是又没有涉及到复杂的数据结构，因为我们矩阵的实现需要用到二维数组，必然涉及到边界值的判断，不限行的话，非常容易数组越界，然后按循环打印又涉及到循环的嵌套。因此我们先用图分析整个打印过程
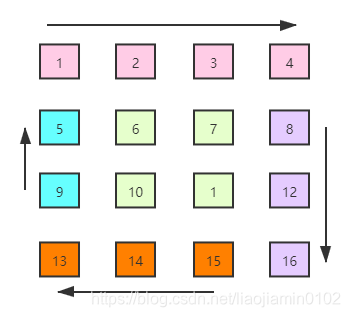
当问题复杂的时候我们可以用图片拆解问题，将复杂问题拆成局部小问题分析，如下，我们用一个循环来打印矩阵，每次分析其中的一个圈。
如上第一圈的遍历，我们假设行数是row，列是col。打印的时候最左上角的坐标应该都是行列都是相同的，例如（0,0），（1,1），（2,2）等。因此我们开始的起点标识为start，那么坐标就是（start，start）
上图中是一个44 的矩阵，最后一圈明显有4个数字起始坐标（1,1），4> 11，但是对于一个55 的矩阵来说，最后一圈就只有一个坐标（2,2），5> 22，对于66 的矩阵最后一圈还是4个，起始坐标还是（2,2），6> 22。我们可以得出，每次的起点位置都是满足 col > startX 2 并且 row > startY2。可以将这个当做循环结束的条件
经如上分析，得出以下实现：

/*** 顺时针打印矩阵* @author liaojiamin* @Date:Created in 11:11 2021/4/2*/
public class PrintMatrix {public static void printMartix(int[][] nums, int col, int row){if(nums == null || row <= 0 || col <= 0){return;}int start = 0;while(col > start*2 && row > start*2){printMartix(nums, col, row, start);start ++;}}
.....
}

接下来实现打印的逻辑。如上图中分析，我们打印可以分为四个部分，：上，右，下，左。每一步我们都更具起始和终止的xy，坐标来循环，那么接下来我们只需要确认四个角的打印开始位置就行。
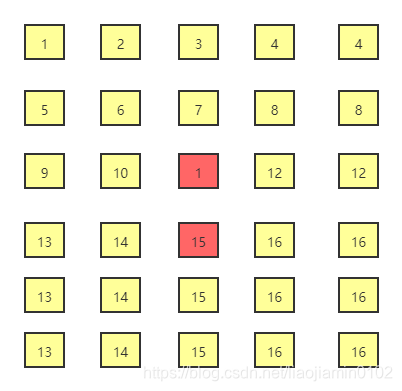
不过应该注意的是，最后一圈不一定是一个圈，或者一个点，可能是一个直线，因为我们以上的案例都是四方的矩阵，还有长方的，例如5*6 的矩阵
如上特殊案例中，我们每次打印之前需要判断，我们的起始坐标（start， start）应该比（endx，endy）都要小
如上分析，我们有如下实现：

 public static void printMartix(int[][] nums, int col, int row, int start){int endx = col-start-1;int endy = row-start-1;for (int i = start; i <= endx; i++) {System.out.print(nums[start][i]);System.out.print(",");}if(start < endy){for(int i = start+1; i<=endy; i++){System.out.print(nums[i][endx]);System.out.print(",");}}if(start < endx && start< endy){for(int i = endx-1;i >=start; i--){System.out.print(nums[endy][i]);System.out.print(",");}}if(start < endx){for(int i = endy - 1; i>=start+1;i--){System.out.print(nums[i][start]);System.out.print(",");}}}public static void main(String[] args) {int row = 10, col = 8;int[][] nums = new int[row][col];for (int i = 0; i < row; i++) {for (int i1 = 0; i1 < col; i1++) {nums[i][i1] = i*i1;System.out.print(i*i1);System.out.print(",");}System.out.println();}System.out.println();printMartix(nums, col, row);}